Жадная гауссова сегментация (GGS) — это решатель Python для эффективной сегментации данных многомерных временных рядов. Подробности реализации см. в нашем документе по адресу http://stanford.edu/~boyd/papers/ggs.html.
Решатель GGS принимает матрицу данных размером n на T и разбивает временные метки T на n-мерном векторе на сегменты, в которых данные хорошо объясняются как независимые выборки из многомерного распределения Гаусса. Для этого он формулирует задачу максимального правдоподобия, регуляризованную по ковариации, и решает ее с помощью жадной эвристики, все подробности которой описаны в статье.
git clone [email protected]:davidhallac/GGS.git
cd GGS
python helloworld.py
ggs.py находится в том же каталоге, что и ваш новый файл, а затем добавьте следующий код в начало вашего скрипта: from ggs import *
Пакет GGS имеет три основные функции:
bps, objectives = GGS(data, Kmax, lamb)
Находит K точек останова в данных для заданного параметра регуляризации лямбда.
Входы
data - матрица данных размером n на T с временными метками T n-мерного вектора
Kmax - количество точек останова, которые нужно найти.
Lamb - параметр регуляризации для регуляризованной ковариации
Возврат
bps — список списков, где элемент i большего списка — это набор точек останова, найденных в K = i в алгоритме GGS.
цели — список целевых значений на каждом промежуточном этапе (от K = 0 до Kmax)
meancovs = GGSMeanCov(data, breakpoints, lamb)
Находит средние значения и регуляризованные ковариации каждого сегмента по набору контрольных точек.
Входы
data - матрица данных размером n на T с временными метками T n-мерного вектора
точки останова — список мест точек останова.
Lamb - параметр регуляризации для регуляризованной ковариации
Возврат
meancovs — список кортежей (среднего значения, ковариации) для каждого сегмента данных.
cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])
Выполняет 10-кратную перекрестную проверку и возвращает вероятность поезда и тестового набора для каждой пары (K, лямбда) до Kmax.
Входы
data - матрица данных размером n на T с временными метками T n-мерного вектора
Kmax — максимальное количество точек останова для запуска GGS.
LambList — список параметров регуляризации для проверки
Возврат
cvResults — список кортежей (lamb, ([TrainLL],[TestLL])) для каждого параметра регуляризации в LambList. Здесь TrainLL и TestLL — это среднее логарифмическое правдоподобие для каждой выборки при 10-кратной перекрестной проверке для всех K от 0 до Kmax.
Дополнительные необязательные параметры (для всех трех вышеперечисленных функций):
Features = [] — выберите определенное подмножество столбцов в данных для работы
verbose = False — печать промежуточных шагов при запуске алгоритма.
financeExample.py даст следующий график, показывающий цель (уравнение 4 в статье) в зависимости от количества точек останова:
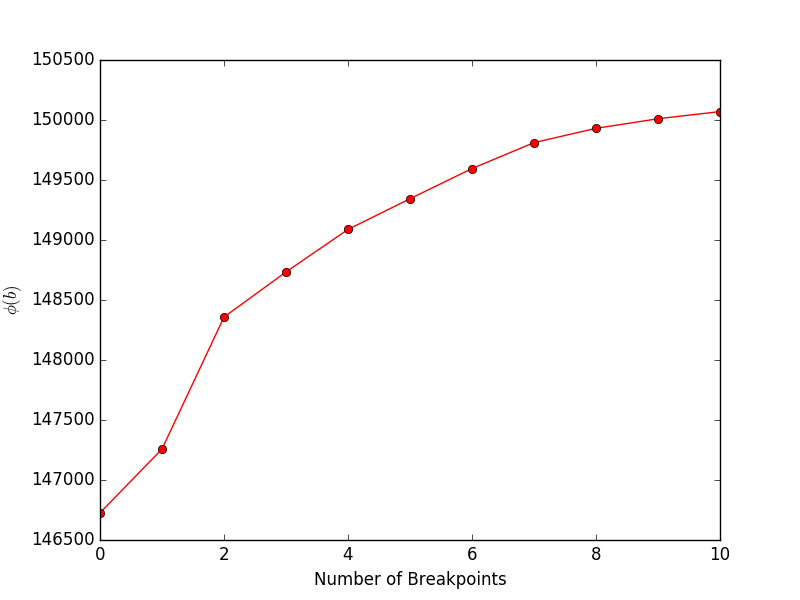
После того, как мы определили расположение точек останова, мы можем использовать функцию FindMeanCovs() чтобы найти средние значения и ковариации каждого сегмента. В примере helloworld.py построение графика средних значений, дисперсий и ковариаций трех сигналов дает:
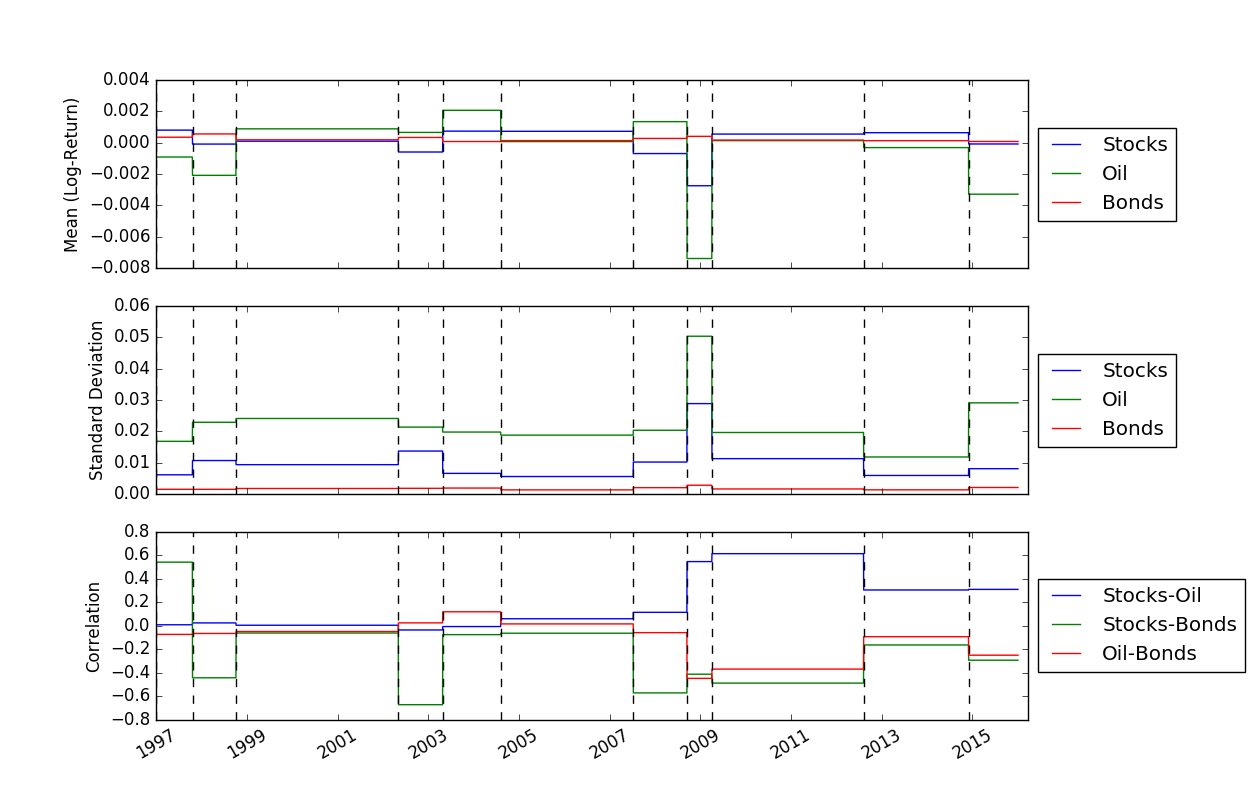
Чтобы запустить перекрестную проверку, которая может быть полезна при определении оптимальных значений K и лямбда, мы можем использовать следующий код для загрузки данных, запуска перекрестной проверки, а затем построить график вероятности теста и обучения:
from ggs import *
import numpy as np
import matplotlib.pyplot as plt
filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]
#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)
trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()
Итоговый график выглядит так:
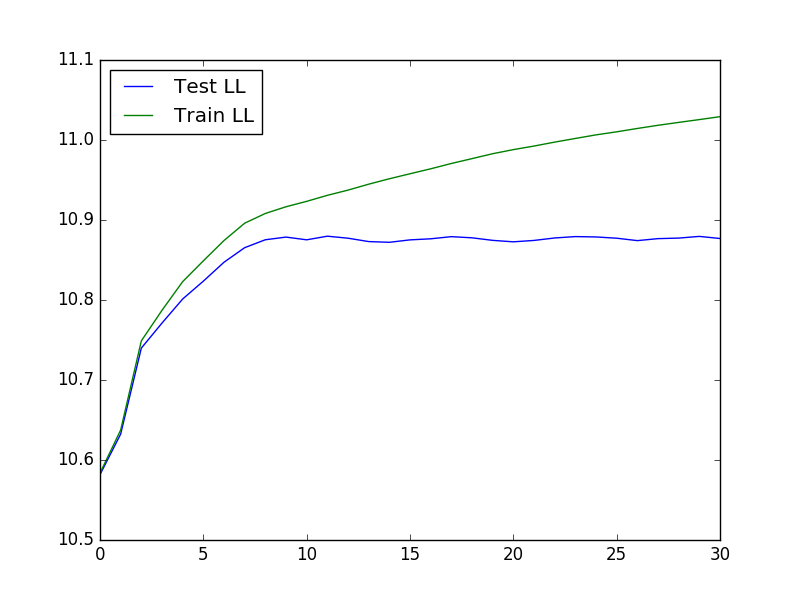
Жадная гауссовая сегментация данных временных рядов - Д. Халлак, П. Ниструп и С. Бойд
Дэвид Халлак, Питер Ниструп и Стивен Бойд.