bosonic

Bosonic: библиотека квантовой оптики

Bosonic — это библиотека, разработанная для моделирования фотонных систем, входными данными которых являются неразличимые бозоны (в случае интереса авторов — фотоны). В частности, он фокусируется на быстром вычислении многочастичных передаточных функций для этих систем и поддерживает вычисление градиента функции стоимости по отношению к параметрам системы. Первоначально он был разработан для разработки наших квантово-оптических нейронных сетей [1] и содержит специализированные функции для их моделирования и оптимизации.

Ключевые направления этой библиотеки были двоякими:

1. Скорость: ключевые функции написаны на оптимизированном Cython с поддержкой многопоточности OpenMP.
2. Повсеместная поддержка autograd: мы в значительной степени полагаемся на использование библиотеки Autograd [1] для вычисления градиентов и эффективной оптимизации параметров системы. Везде, где оптимизированные функции прямого прохода написаны на Cython, также должна быть явная поддержка кода autograd. В настоящее время это не всегда так, но есть поддержка всех основных функций.

Ключевая функциональность

Многочастичная унитарная эволюция

Основной мотивацией для этого пакета было быстрое вычисление многочастичного унитарного преобразования как функции одночастичного унитарного преобразования и количества бозонных входов. То есть, если у нас есть четырехмерный унитарный U и мы знаем, что на входе находятся 3 фотона, мы хотим знать преобразование по $binom{4+3-1, 3}$ -мерный базис $[3,0,0,0], [2,1,0,0], [2,0,1,0], ... и т.д.

Это подтверждается функцией bosonic.aa_phi , названной в честь Ааронсона и Архипова, которые указали вид этой функции, которую мы используем в качестве своей функции Φ(U) в [2]. Например, мы можем продемонстрировать знаменитый эффект Хонг-У-Манделя с помощью светоделителя:

 >> > import bosonic as b
>> > import numpy as np
>> > U = np . array ([[ 1 , 1 ], [ 1 , - 1 ]], dtype = complex ) / np . sqrt ( 2 )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU )
[[ 0.5       + 0.j  0.70710678 + 0.j  0.5       + 0.j ]
 [ 0.70710678 + 0.j  0.        + 0.j - 0.70710678 + 0.j ]
 [ 0.5       + 0.j - 0.70710678 + 0.j  0.5       + 0.j ]]
>> > print ( b . fock . basis ( 2 , 2 ))
[[ 2 , 0 ], [ 1 , 1 ], [ 0 , 2 ]]
>> > input = np . array ([[ 0 ], [ 1 ], [ 0 ]], dtype = complex )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU . dot ( input ))
[[ 0.70710678 + 0.j ]
 [ 0.        + 0.j ]
 [ - 0.70710678 + 0.j ]]
 >> > print ( np . abs ( phiU . dot ( input )) ** 2 )
[[ 0.5 ]
 [ 0. ]
 [ 0.5 ]]

Здесь мы строим унитарный модуль, соответствующий светоделителю 50/50 в U. Как показано в строке после того, как мы напечатали phiU, базисом здесь являются [2, 0], [1, 1] и [0, 2]. Таким образом, состояние, соответствующее одному фотону, падающему на каждый из входов, равно [0, 1, 0]. В последней строке (две строки) мы видим, что выходной сигнал представляет собой равную суперпозицию двух фотонов на одном выходе и двух фотонов на другом, без вероятности того, что фотоны уйдут через разные порты.

Квантовые оптические нейронные сети

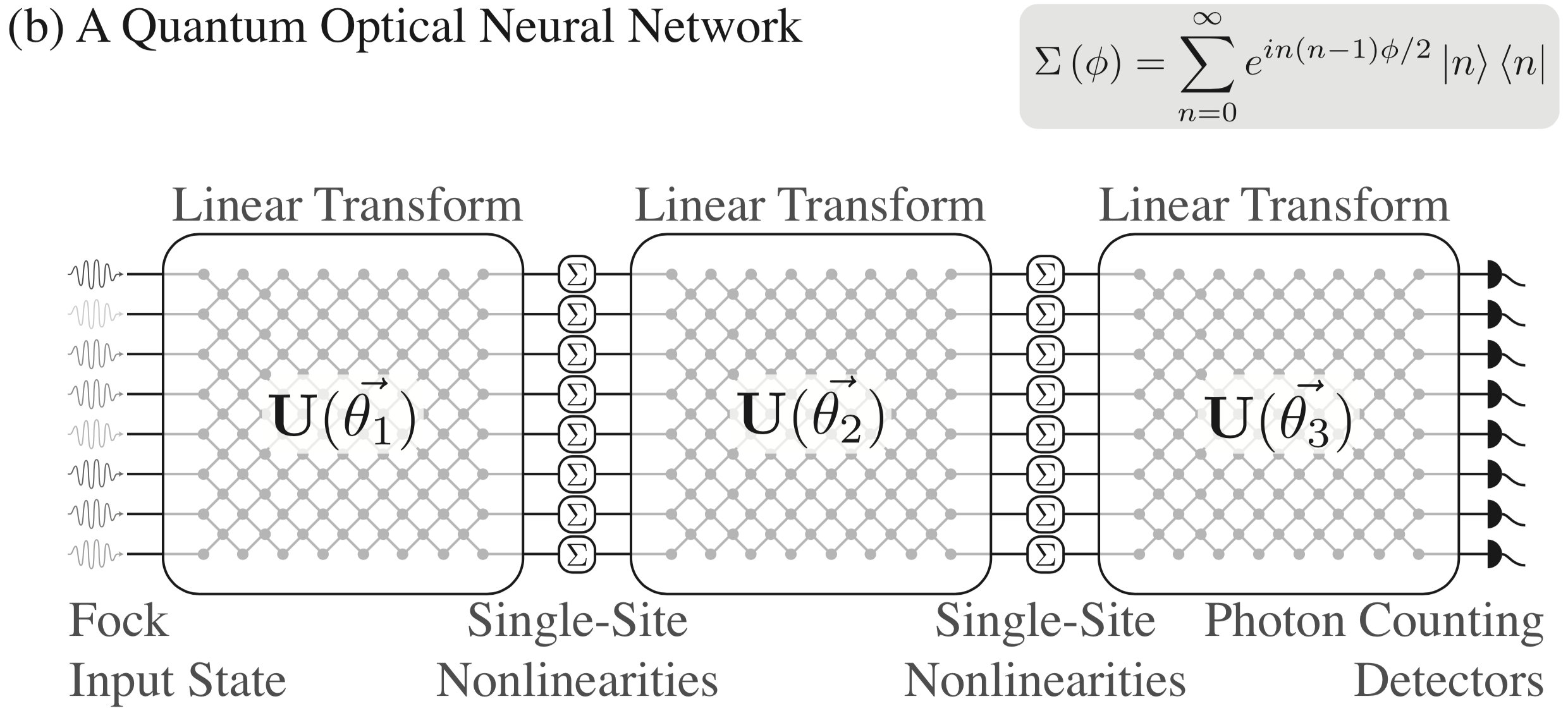
Как описано в [1], мы разработали предлагаемую архитектуру квантовых оптических нейронных сетей, которая включает в себя мозаику произвольных унитарных преобразований с одноузловыми нелинейностями. Более подробную информацию см. в статье, а вот визуальное описание архитектуры:

Установка

Клонирование этого репозитория на данный момент является единственным способом установить bosonic в вашей системе. Прежде чем сделать это, вам понадобится установленный пакет Python Cython для правильной сборки bosonic . Что-то вроде этого должно работать в Linux (при желании используйте предпочитаемый вами менеджер пакетов Python вместо pip ):

$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .

На Mac вам также понадобятся gcc из homebrew и libopenmp:

$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install .

После этого вы сможете проверить правильность установки bosonic , запустив

$ python setup.py test

Ссылки

[1] Штайнбрехер, Г.Р., Олсон, Дж.П., Энглунд, Д., и Кэролан, Дж. (2018). Квантовые оптические нейронные сети. Препринт arXiv arXiv:1808.10047. https://arxiv.org/abs/1808.10047

[2] Ааронсон, Скотт и Алекс Архипов. «Вычислительная сложность линейной оптики». Материалы сорок третьего ежегодного симпозиума ACM по теории вычислений. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf.