

Пакет FRK доступен на CRAN! Для установки введите
install.packages( " FRK " ) Чтобы установить самую последнюю версию разработки, загрузите devtools и введите
install_github( " andrewzm/FRK " , dependencies = TRUE , build_vignettes = TRUE )Документ, представляющий пакет, доступен здесь. Документ, подробно описывающий подход в негауссовых условиях, доступен здесь (шестистраничное резюме этой статьи доступно здесь).
Виньетка «FRK_intro» обобщает пакет, дает подробную информацию об алгоритме EM, который может быть использован в гауссовой настройке, и предоставляет несколько примеров. Другая виньетка, «FRK_non-Gaussian», обобщает выводы в негауссовых условиях (где используется аппроксимация Лапласа) и содержит примеры с использованием негауссовских данных и новых доступных методов построения графиков. Чтобы получить доступ к виньеткам, нажмите на следующие ссылки:
Введение в ФРК
Учебное пособие по моделированию пространственных и пространственно-временных негауссовских данных с помощью FRK
Страница pkgdown также доступна здесь.
Если вы используете FRK в своей работе, исследованиях или другой деятельности, пожалуйста, цитируйте его, используя информацию, предоставленную citation("FRK") .
Пакет: ФРК
Тип: Пакет
Название: Кригинг фиксированного ранга
Версия: 2.3.1
Дата: 16 июля 2024 г.
Автор: Эндрю Заммит-Мангион, Мэтью Сейнсбери-Дейл
Сопровождающий: Эндрю Заммит-Мангион [email protected]
Описание: Инструмент для пространственного/пространственно-временного моделирования и прогнозирования с большими наборами данных. Этот подход моделирует поле и, следовательно, ковариационную функцию, используя набор базисных функций. Такое представление базисной функции фиксированного ранга облегчает моделирование больших данных, и этот метод, естественно, допускает нестационарные анизотропные ковариационные функции. Дискретизация пространственной области на так называемые базовые единицы площади (BAU) облегчает использование наблюдений с различной поддержкой (т. е. как точечной, так и площадной поддержкой, возможно одновременно), а также прогнозирование по произвольным регионам, указанным пользователем. FRK также поддерживает логические выводы по различным многообразиям, включая 2D-плоскость и 3D-сферу, и предоставляет вспомогательные функции для сравнительно легкого моделирования, подбора, прогнозирования и построения графиков. Версия 2.0.0 и выше также поддерживает моделирование негауссовских данных (например, пуассоновских, биномиальных, отрицательно-биномиальных, гамма- и обратно-гауссовских данных) с использованием структуры обобщенной линейной смешанной модели (GLMM). Заммит-Мангион и Кресси (2021) описывают FRK в гауссовском методе и подробно описывают использование базисных функций и BAU, а Sainsbury-Dale et al. (2024) описывают FRK в негауссовой ситуации; Доступны две виньетки, в которых суммируются эти статьи и приводятся дополнительные примеры.
Лицензия: GPL (>= 2)
library( " FRK " )
library( " sp " )
library( " ggplot2 " )
library( " ggpubr " )
# # Setup
m <- 1000 # Sample size
RNGversion( " 3.6.0 " ); set.seed( 1 ) # Fix seed
zdf <- data.frame ( x = runif( m ), y = runif( m )) # Generate random locs
zdf $ z <- sin( 8 * zdf $ x ) + cos( 8 * zdf $ y ) + 0.5 * rnorm( m ) # Simulate data
coordinates( zdf ) = ~ x + y # Turn into sp object
# # Run FRK
S <- FRK( f = z ~ 1 , # Formula to FRK
list ( zdf ), # All datasets are supplied in list
n_EM = 10 ) # Max number of EM iterations
pred <- predict( S ) # Prediction stage
# # Plotting
plotlist <- plot( S , pred )
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )
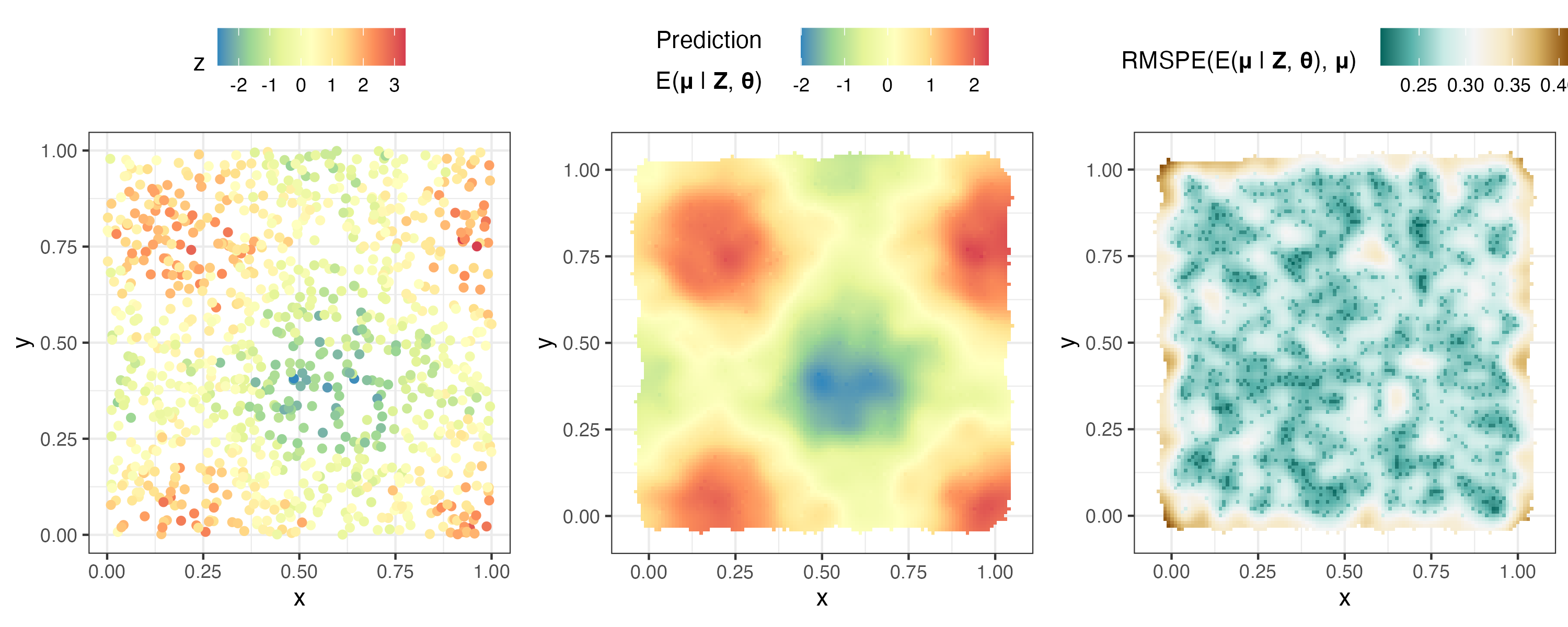
Здесь мы анализируем смоделированные данные Пуассона. Мы обозначаем модель данных Пуассона со средним откликом, который моделируется с использованием функции связи квадратного корня, устанавливая response = "poisson" и link = "sqrt" в FRK() . Другими негауссовскими распределениями отклика, доступными в FRK являются биномиальное, отрицательно-биномиальное, гамма-распределение и обратное гауссово распределение.
# # Simulate Poisson data using the previous example's data to construct a mean
zdf $ z <- rpois( m , lambda = zdf $ z ^ 2 )
# # Run FRK
S <- FRK( f = z ~ 1 , list ( zdf ),
response = " poisson " , # Poisson data model
link = " sqrt " ) # square-root link function
pred <- predict( S )
# # Plotting
plotlist <- plot( S , pred $ newdata )
ggarrange( plotlist $ z , plotlist $ p_mu , plotlist $ interval90_mu ,
nrow = 1 , legend = " top " )
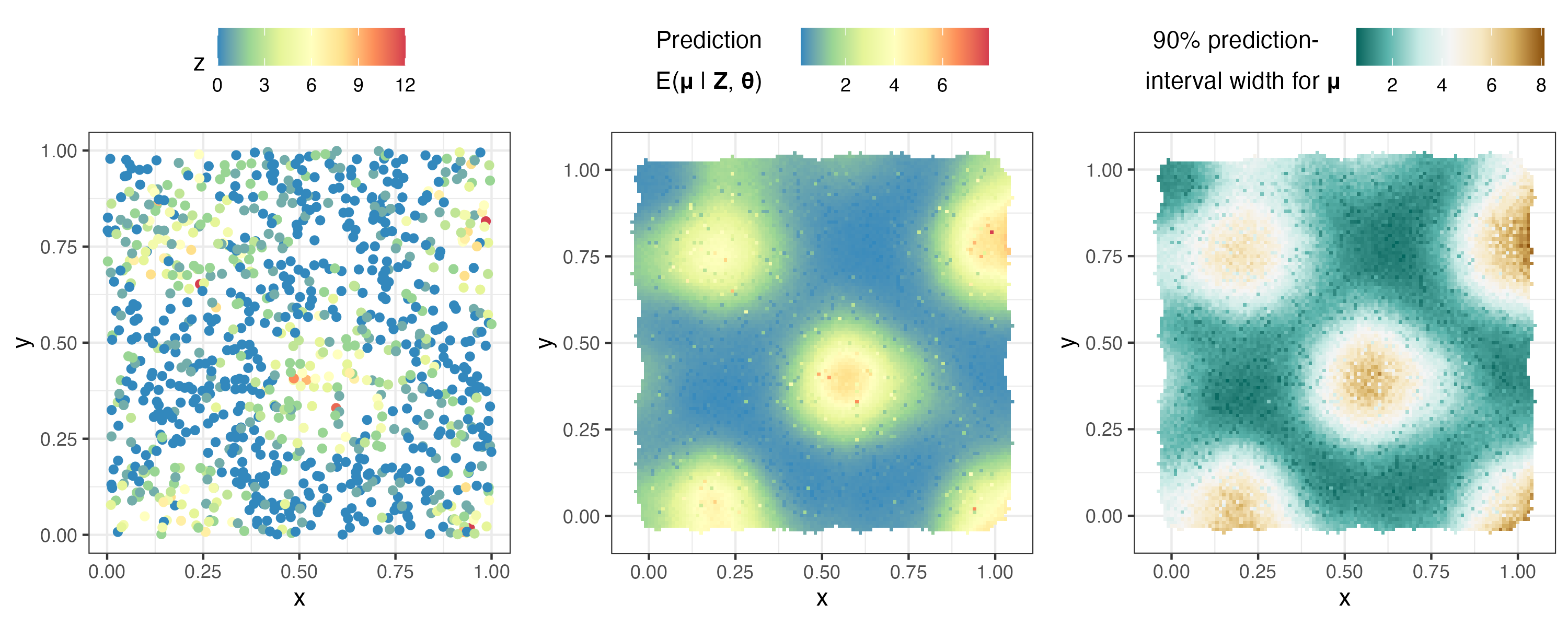
Теперь мы анализируем пространственно-временные данные, используя набор данных NOAA.
# # Setup
library( " spacetime " )
data( " NOAA_df_1990 " )
Tmax <- subset( NOAA_df_1990 , month %in% 7 & year == 1993 )
Tmax <- within( Tmax , { time = as.Date(paste( year , month , day , sep = " - " ))})
STObj <- stConstruct( x = Tmax , space = c( " lon " , " lat " ), time = " time " , interval = TRUE )
# # BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs( manifold = STplane(),
cellsize = c( 1 , 1 , 1 ),
data = STObj , tunit = " days " )
BAUs $ fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
# # Basis functions
G <- auto_basis( manifold = STplane(), data = STObj , nres = 2 , tunit = " days " )
# # Run FRK
STObj $ std <- 2 # fix the measurement error variance
S <- FRK( f = z ~ 1 + lat , data = list ( STObj ),
basis = G , BAUs = BAUs , est_error = FALSE , method = " TMB " )
pred <- predict( S , percentiles = NULL )
# # Plotting: include only some times via the argument subset_time
plotlist <- plot( S , pred $ newdata , subset_time = c( 1 , 7 , 13 , 19 , 25 , 31 ))
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )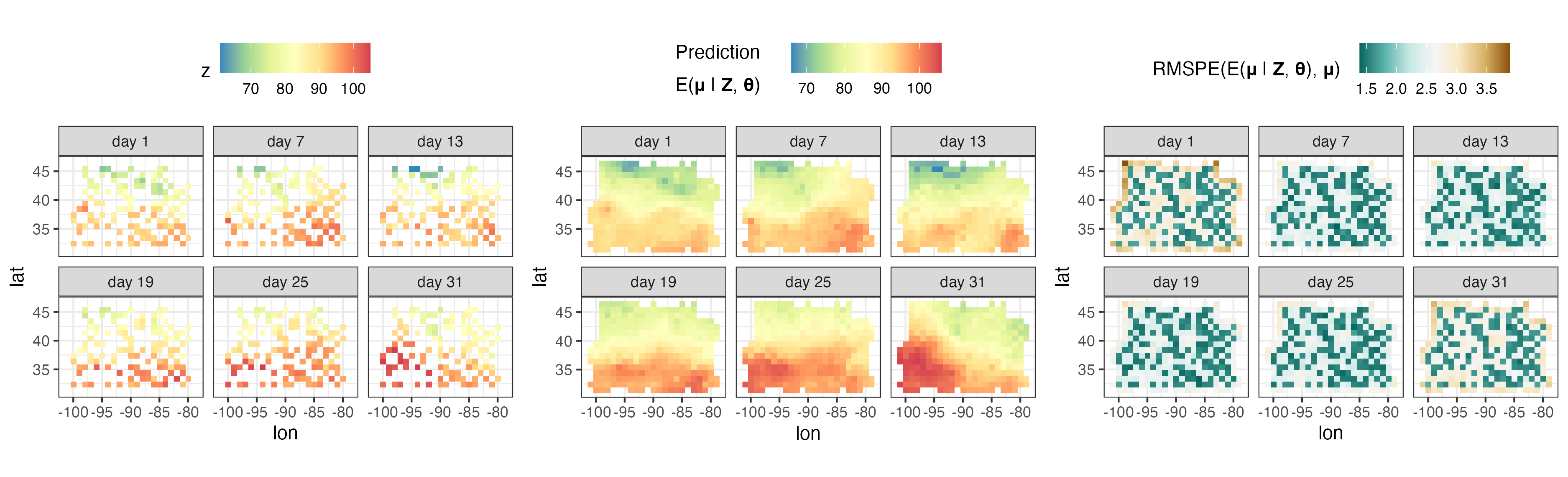
Пакет FRK в настоящее время используется для создания пространственно-временной анимации полей, наблюдаемых по спутниковым данным. Здесь мы показываем ежедневный прогноз содержания CO2 с использованием данных НАСА OCO-2 в период с сентября 2014 года по июнь 2016 года.
Спасибо Майклу Бертолаччи за разработку шестигранного логотипа FRK!