greta.gam позволяет использовать более плавные функции и синтаксис формул mgcv для определения плавных терминов для использования в модели greta. Затем вы можете определить свою собственную вероятность завершения модели и подогнать ее с помощью MCMC.
Это работа в процессе!
Вот простой пример, адаптированный из файла справки mgcv ?gam :
В mgcv :
library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )
# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model
# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat ) Теперь примеряю ту же модель в greta :
library( greta.gam )
# > Loading required package: greta
# >
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# >
# > binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# >
# > %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# > eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# > tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!
# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )
# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))
# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )
# build model
m <- model( z_pred )
# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#> warmup 0/1000 | eta: ?s warmup == 50/1000 | eta: 30s warmup ==== 100/1000 | eta: 17s warmup ====== 150/1000 | eta: 12s warmup ======== 200/1000 | eta: 10s warmup ========== 250/1000 | eta: 8s warmup =========== 300/1000 | eta: 7s warmup ============= 350/1000 | eta: 6s warmup =============== 400/1000 | eta: 5s warmup ================= 450/1000 | eta: 5s warmup =================== 500/1000 | eta: 4s warmup ===================== 550/1000 | eta: 4s warmup ======================= 600/1000 | eta: 3s warmup ========================= 650/1000 | eta: 3s warmup =========================== 700/1000 | eta: 2s warmup ============================ 750/1000 | eta: 2s warmup ============================== 800/1000 | eta: 1s warmup ================================ 850/1000 | eta: 1s warmup ================================== 900/1000 | eta: 1s warmup ==================================== 950/1000 | eta: 0s warmup ====================================== 1000/1000 | eta: 0s
# > sampling 0/200 | eta: ?s sampling ========== 50/200 | eta: 1s sampling =================== 100/200 | eta: 0s sampling ============================ 150/200 | eta: 0s sampling ====================================== 200/200 | eta: 0s
# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])
# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL
# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )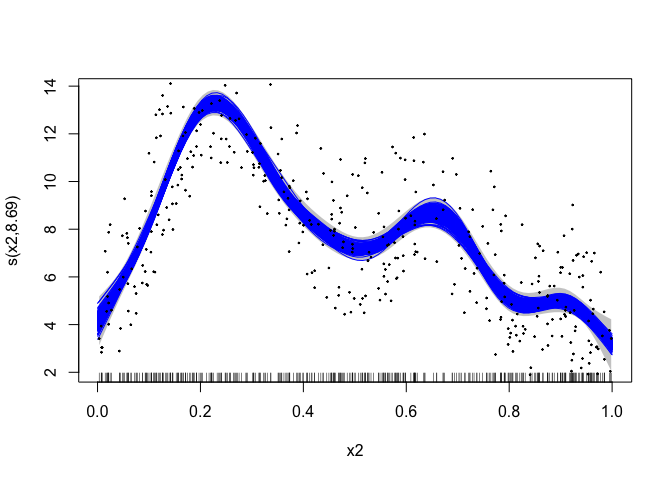
greta.gam использует несколько приемов из программы jagam (Wood, 2016) в mgcv чтобы заставить все работать. Вот некоторые краткие подробности для тех, кто интересуется внутренней работой…
GAM — это модели с байесовскими интерпретациями (даже при использовании «частотных» методов). Более гладкую матрицу штрафов можно рассматривать как матрицу априорной точности в байесовской модели случайных эффектов. Матрицы расчета строятся точно так же, как и в частотном случае. Дополнительную информацию по этому вопросу см. в Miller (2021).
В байесовской интерпретации GAM есть небольшая трудность, заключающаяся в том, что в своей наивной форме априорные значения являются неподходящими в качестве нулевого пространства штрафа (в одномерном случае обычно это линейный член). Чтобы получить правильные априоры, мы можем использовать один из «трюков», использованных в работе Марра и Вуда (2011), а именно каким-то образом наказать те части штрафа, которые приводят к неправильному априорному результату. Мы берем вариант, предоставляемый jagam , и создаем дополнительную матрицу штрафов для этих членов (из собственного разложения матрицы штрафов; см. Marra & Wood, 2011).
Марра, Г. и Вуд, С.Н. (2011)Практический выбор переменных для обобщенных аддитивных моделей. Вычислительная статистика и анализ данных, 55, 2372–2387.
Миллер Д.Л. (2021). Байесовские взгляды на обобщенное аддитивное моделирование. arXiv.
Вуд, С.Н. (2016) Еще один разработчик аддитивного моделирования Гиббса: взаимодействие JAGS и mgcv. Журнал статистического программного обеспечения 75, вып. 7