

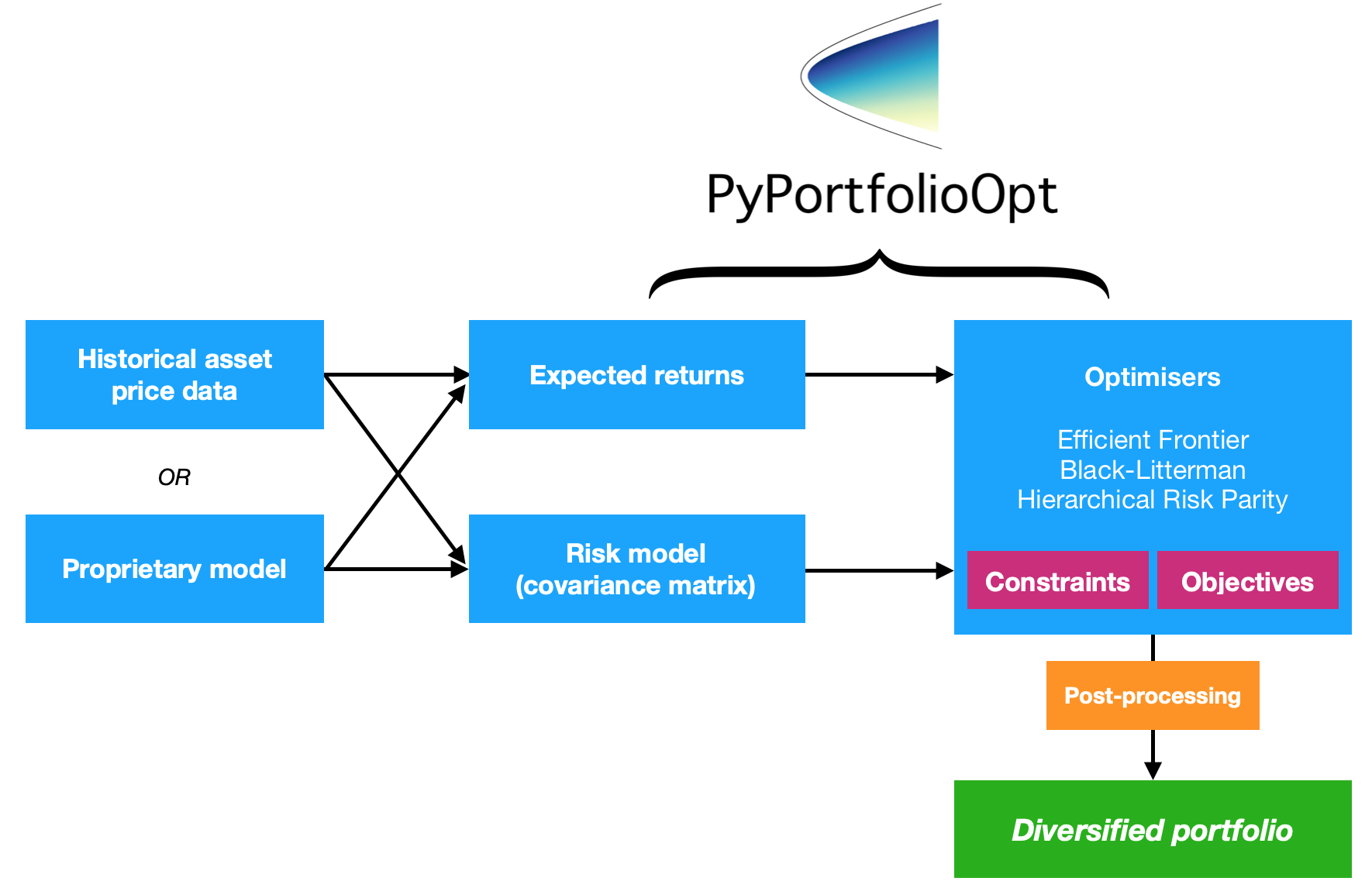
PyPortfolioOpt — это библиотека, реализующая методы оптимизации портфеля, включая классические методы оптимизации среднего отклонения и распределение Блэка-Литтермана, а также более поздние разработки в этой области, такие как сокращение и иерархическая паритет рисков.
Он обширен , но легко расширяем и может быть полезен как обычным инвесторам, так и профессионалам, которым нужен простой инструмент для прототипирования. Независимо от того, являетесь ли вы инвестором, ориентированным на фундаментальные факторы, который определил несколько недооцененных вариантов, или алгоритмическим трейдером, у которого есть корзина стратегий, PyPortfolioOpt может помочь вам объединить ваши альфа-источники наиболее эффективным с точки зрения риска способом.
PyPortfolioOpt был опубликован в Журнале программного обеспечения с открытым исходным кодом?
PyPortfolioOpt теперь поддерживается Туаном Траном.
Перейдите к документации ReadTheDocs, чтобы более подробно изучить проект, или ознакомьтесь с кулинарной книгой, чтобы увидеть несколько примеров, демонстрирующих полный процесс от загрузки данных до создания портфолио.
Если вы хотите интерактивно поиграть с PyPortfolioOpt в браузере, вы можете запустить Binder здесь. Настройка занимает некоторое время, но позволяет опробовать рецепты кулинарной книги без необходимости выполнять все требования.
Примечание. Пользователям macOS необходимо установить инструменты командной строки.
Примечание. Если вы используете Windows, сначала необходимо установить C++. (скачать, установить инструкцию)
Этот проект доступен на PyPI, а это означает, что вы можете просто:
pip install PyPortfolioOpt(возможно, вам придется следовать отдельным инструкциям по установке cvxopt и cvxpy).
Однако лучше всего использовать диспетчер зависимостей в виртуальной среде. Моя текущая рекомендация — заняться поэзией, а затем просто бежать.
poetry add PyPortfolioOptВ противном случае клонируйте/загрузите проект и в каталоге проекта запустите:
python setup.py install PyPortfolioOpt поддерживает Docker. Создайте свой первый контейнер с помощью docker build -f docker/Dockerfile . -t pypfopt . Вы можете использовать этот образ для запуска тестов или даже запуска сервера Jupyter.
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bashДля получения дополнительной информации, пожалуйста, прочитайте это руководство.
Если вы хотите внести серьезные изменения для интеграции с вашей собственной системой, вероятно, имеет смысл клонировать этот репозиторий и просто использовать исходный код.
git clone https://github.com/robertmartin8/PyPortfolioOptАльтернативно, вы можете попробовать:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.gitВот пример реальных данных об акциях, демонстрирующий, как легко найти портфель только для длинных позиций, который максимизирует коэффициент Шарпа (показатель доходности с поправкой на риск).
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )Это выводит следующие веса:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28Это интересно, но само по себе бесполезно. Однако PyPortfolioOpt предоставляет метод, который позволяет вам конвертировать вышеуказанные непрерывные веса в фактическое распределение, которое вы можете купить. Просто введите самые последние цены и желаемый размер портфеля (в данном примере 10 000 долларов США):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89Отказ от ответственности: ничто в этом проекте не является инвестиционным советом, и автор не несет ответственности за ваши последующие инвестиционные решения. Пожалуйста, обратитесь к лицензии для получения дополнительной информации.
Статья Гарри Марковица 1952 года является неоспоримой классикой, которая превратила оптимизацию портфеля из искусства в науку. Ключевой вывод заключается в том, что, комбинируя активы с различной ожидаемой доходностью и волатильностью, можно принять решение о математически оптимальном распределении, которое минимизирует риск для целевой доходности – набор всех таких оптимальных портфелей называется эффективной границей .
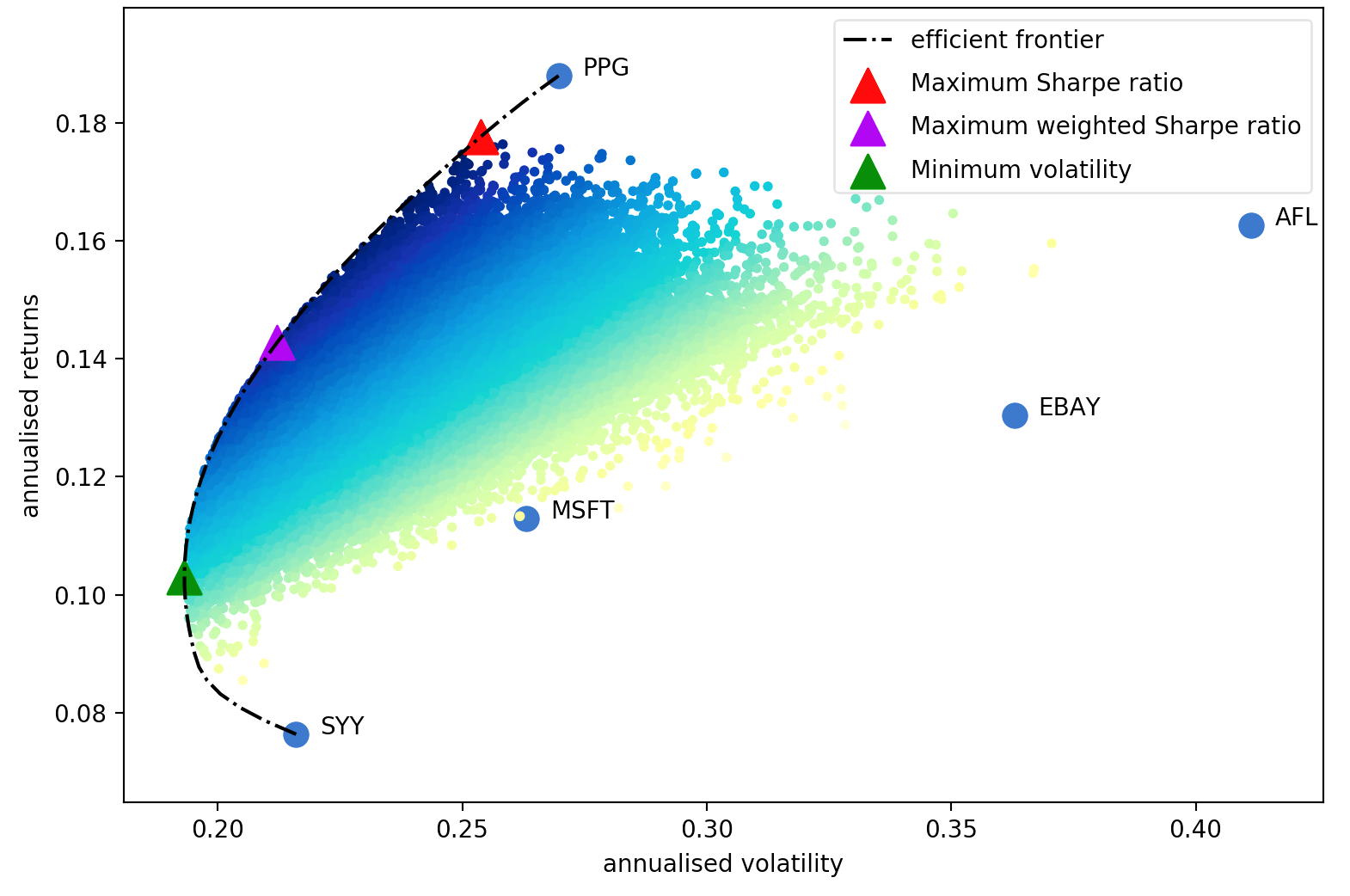
Несмотря на то, что в этом вопросе было достигнуто значительное развитие, более чем полвека спустя основные идеи Марковица по-прежнему фундаментально важны и ежедневно используются во многих фирмах по управлению портфелями. Основным недостатком оптимизации среднего отклонения является то, что теоретическая обработка требует знания ожидаемой доходности и будущих характеристик риска (ковариации) активов. Очевидно, если бы мы знали ожидаемую доходность акций, жизнь была бы намного проще, но вся суть в том, что доходность акций, как известно, трудно прогнозировать. Вместо этого мы можем получить оценки ожидаемой доходности и ковариации на основе исторических данных – хотя мы теряем теоретические гарантии, предоставленные Марковицем, чем ближе наши оценки к реальным значениям, тем лучше будет наш портфель.
Таким образом, этот проект предоставляет четыре основных набора функций (хотя, конечно, они тесно связаны):
Ключевой целью разработки PyPortfolioOpt является модульность : пользователь должен иметь возможность заменять свои компоненты, при этом используя структуру, предоставляемую PyPortfolioOpt.
В этом разделе мы подробно описываем некоторые доступные функции PyPortfolioOpt. Дополнительные примеры можно найти в блокнотах Jupyter здесь. Еще один хороший ресурс — тесты.
Гораздо более полную версию можно найти на ReadTheDocs, а также возможные расширения для более опытных пользователей.
Ковариационная матрица кодирует не только волатильность актива, но и то, как он коррелирует с другими активами. Это важно, поскольку для того, чтобы воспользоваться преимуществами диверсификации (и, таким образом, увеличить доход на единицу риска), активы в портфеле должны быть как можно более некоррелированными.
sklearn.covariance .constant_variance , single_factor и constant_correlation .sklearn.covariance 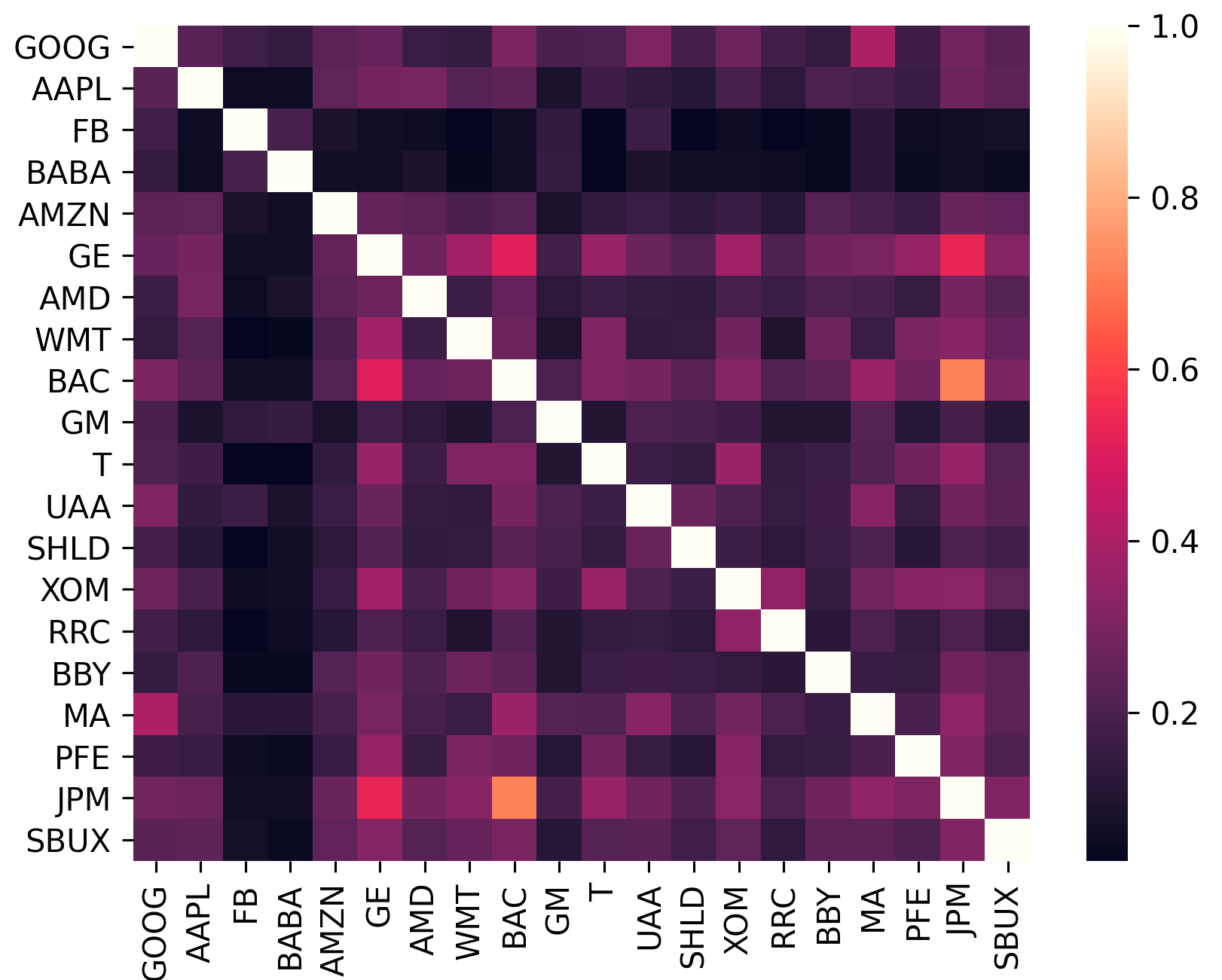
(Этот график был создан с plotting.plot_covariance )
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk и efficient_return PyPortfolioOpt предоставляет возможность сформировать рыночно-нейтральный портфель (т. е. сумма весов равна нулю). Это невозможно для портфеля Шарпа с максимальной и минимальной волатильностью, поскольку в этих случаях они не инвариантны относительно кредитного плеча. Рыночная нейтральность требует отрицательных весов: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 )) Одна из проблем оптимизации среднего отклонения заключается в том, что она приводит к множеству нулевых весов. Хотя они являются «оптимальными» в выборке, существует большое количество исследований, показывающих, что эта характеристика приводит к тому, что портфели со средней дисперсией уступают по эффективности вне выборки. С этой целью я ввел целевую функцию, которая может уменьшить количество пренебрежимо малых весов для любой из целевых функций. По сути, он добавляет штраф (параметризованный gamma ) за малые веса с термином, который выглядит точно так же, как регуляризация L2 в машинном обучении. Возможно, потребуется попробовать несколько значений gamma , чтобы получить желаемое количество весов, которыми можно пренебречь. Для тестового портфеля из 20 ценных бумаг достаточно gamma ~ 1
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()Начиная с версии 0.5.0, мы теперь поддерживаем распределение активов по Блэк-Литтерману, которое позволяет вам комбинировать априорную оценку доходности (например, подразумеваемую рынком доходность) с вашими собственными взглядами для формирования апостериорной оценки. Это приводит к гораздо более точным оценкам ожидаемой доходности, чем просто использование средней исторической доходности. Ознакомьтесь с документацией для обсуждения теории, а также советов по форматированию входных данных.
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe () Вышеупомянутые функции в основном относятся к решению задач оптимизации среднего отклонения с помощью квадратичного программирования (хотя об этом заботится cvxpy ). Однако мы также предлагаем различные оптимизаторы:
Пожалуйста, обратитесь к документации для получения дополнительной информации.
Тесты написаны на pytest (на мой взгляд, гораздо более интуитивно понятно, чем unittest и его варианты), и я постарался обеспечить почти 100% покрытие. Запустите тесты, перейдя в каталог пакета и просто запустив pytest в командной строке.
PyPortfolioOpt предоставляет тестовый набор данных ежедневной доходности для 20 тикеров:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]Эти тикеры были неофициально выбраны по нескольким критериям:
В настоящее время тесты не исследовали все крайние случаи и комбинации целевых функций и параметров. Однако каждый метод и параметр были протестированы на правильную работу.
Если вы используете PyPortfolioOpt для опубликованных работ, цитируйте статью JOSS.
Строка цитирования:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
БибТекс::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}Вклады приветствуются . Дополнительную информацию можно найти в Руководстве по вкладу.
Я хотел бы поблагодарить всех, кто внес свой вклад в PyPortfolioOpt с момента его выпуска в 2018 году. Особые пожелания: