Главная | Установка | Документация | Учебное пособие | Разработчики
Rodeo — это быстрая библиотека Python, которая использует вероятностные числа для решения обыкновенных дифференциальных уравнений (ОДУ). То есть большинство решателей ОДУ (таких как метод Эйлера) создают детерминированную аппроксимацию ОДУ на сетке с размером шага.
Rodeo предоставляет легкое и расширяемое семейство аппроксимаций парадигмы нелинейной байесовской фильтрации, общей для многих вероятностных решателей (Tronarp et al (2018)). Это начинается с помещения гауссовского процесса перед решением ОДУ и его последовательного обновления по мере того, как решатель проходит через сетку. Rodeo построен на jax , который позволяет осуществлять своевременную компиляцию и автоматическую дифференциацию. API jax почти эквивалентен API numpy .
Rodeo предоставляет два основных инструмента: один для аппроксимации решения ОДУ, а другой для вывода параметров. Для первых мы предоставляем:
solve : реализация вероятностного решателя ОДУ, который использует парадигму нелинейной байесовской фильтрации.Для последнего мы предлагаем методы аппроксимации правдоподобия:
basic : реализация базового метода аппроксимации правдоподобия (подробности можно найти в Wu and Lysy (2023)).fenrir : реализация Fenrir (Tronarp et al (2022)).marginal_mcmc : реализация MCMC метода Чкребти (Chkrebtii et al (2016)).dalton : Реализация нашей адаптивной к данным аппроксимации правдоподобия ОДУ (Ву и Лиси (2023)).Подробные примеры их использования можно найти в разделе «Документация». Обратите внимание, что это версия родео только для jax . Информацию об устаревших версиях, использующих различные другие серверные части, см. здесь.
Загрузите репозиторий с GitHub, а затем установите его с помощью сценария setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Сначала перейдите на страницу readthedocs, чтобы просмотреть документацию для следующих примеров.
Краткое руководство по решению простой задачи ОДУ.
Пример решения ОДУ высшего порядка.
Пример решения сложной хаотической ОДУ.
Пример задачи вывода параметров, в которой мы используем приближение Лапласа.
В этом пошаговом руководстве мы покажем, как решать ОДУ с помощью нашего вероятностного решателя, а также проводить вывод параметров. Сначала мы проиллюстрируем схему решения ОДУ. С этой целью давайте рассмотрим следующий пример первого упорядоченного ОДУ (модель ФитцХью-Нагумо ):
где решение
Следуя обозначениям (Ву и Лысый (2023)), имеем
для
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Мы сравниваем решение решателя с детерминированным решением, предоставленным odeint в библиотеке scipy .
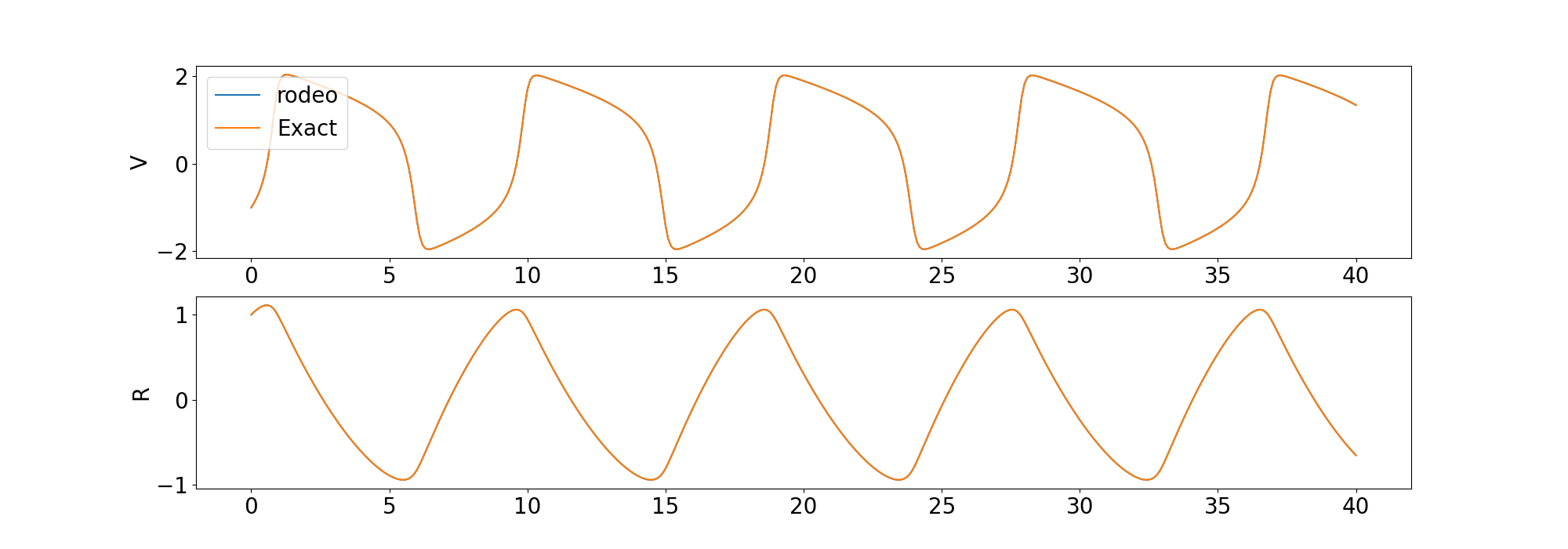
Мы также включаем примеры решения ОДУ более высокого порядка и хаотического ОДУ.
Теперь мы переходим к задаче вывода параметров. Rodeo содержит несколько методов аппроксимации правдоподобия, которые обобщены в разделе «Описание». Здесь мы будем использовать basic метод аппроксимации правдоподобия. Предположим, что наблюдения моделируются с помощью модели
где basic приближения правдоподобия для
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Это базовый пример для демонстрации использования. Мы предлагаем более сложные аппроксимации правдоподобия, которые распространяют неопределенность решения на аппроксимацию правдоподобия, такие как fenrir , marginal_mcmc и dalton . Для получения более подробной информации обратитесь к руководству по выводу параметров.
Вот некоторые результаты, полученные с помощью различных приближений правдоподобия, найденных в родео из /examples/ :
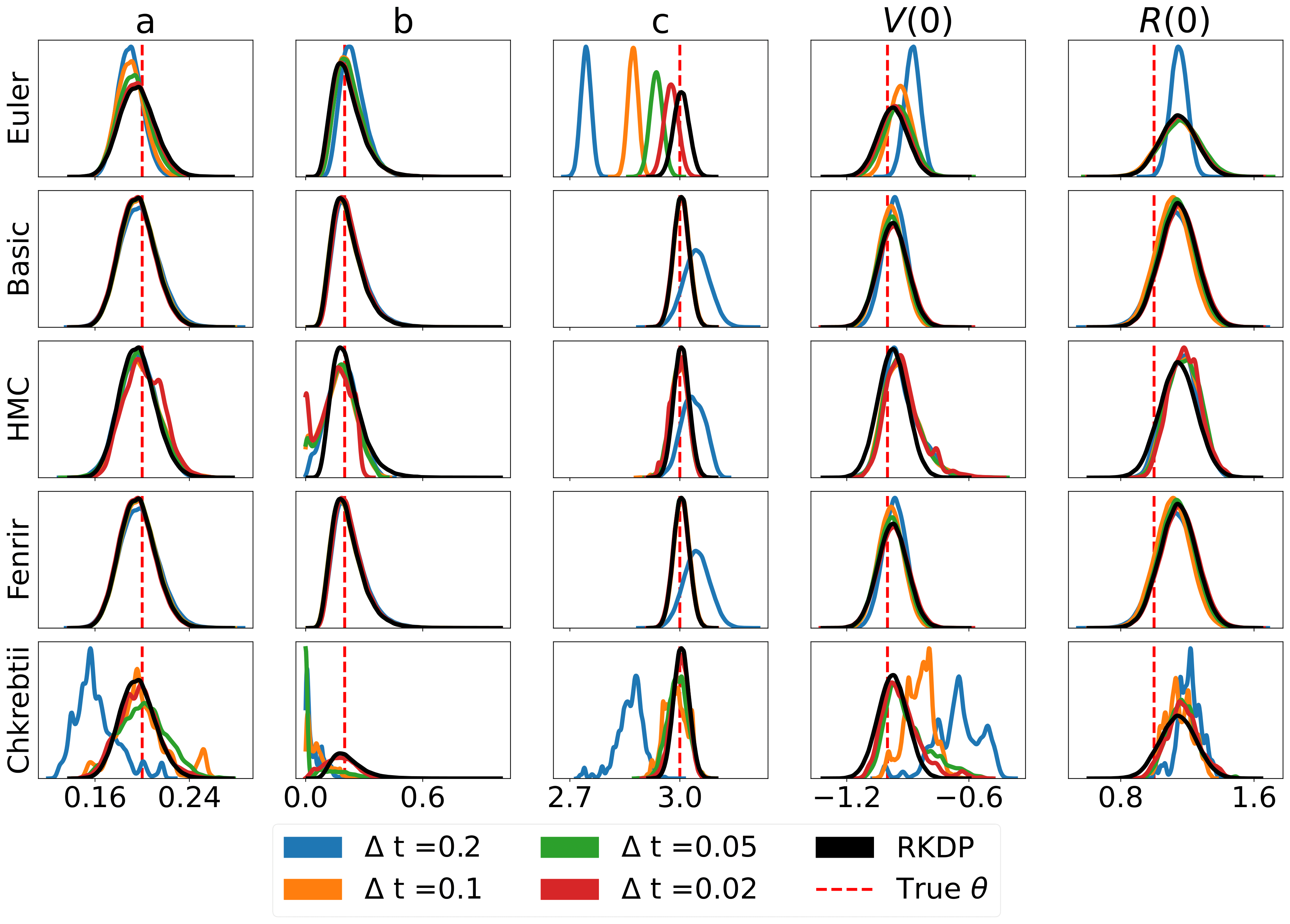
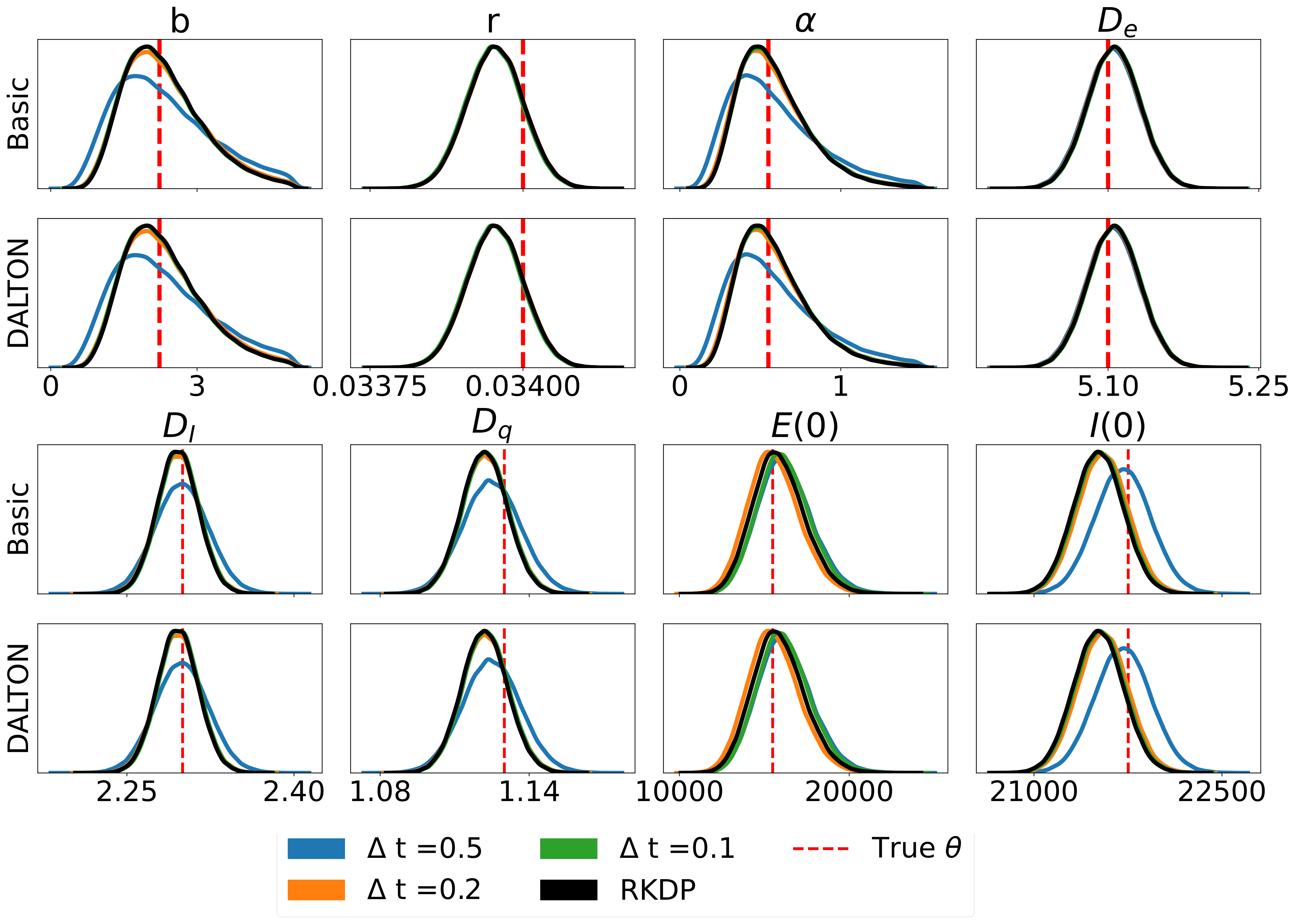
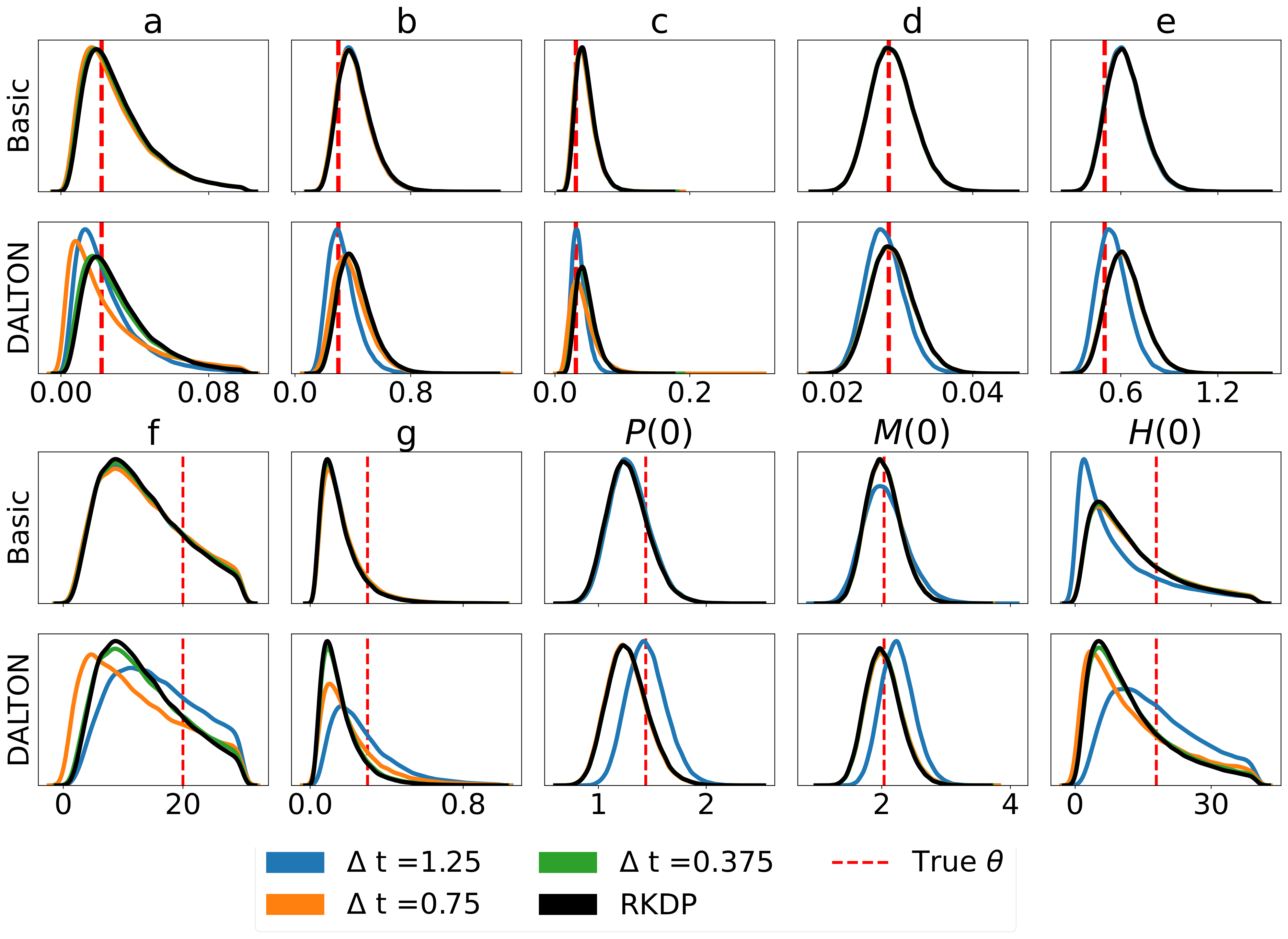
Юнит-тесты можно запустить с помощью следующих команд:
cd tests
python -m unittest discover -v Или установите tox , затем изнутри rodeo введите командную строку: tox .
HTML-документацию можно скомпилировать из корневой папки:
pip install .[docs]
cd docs
make html Это создаст документацию в docs/build .