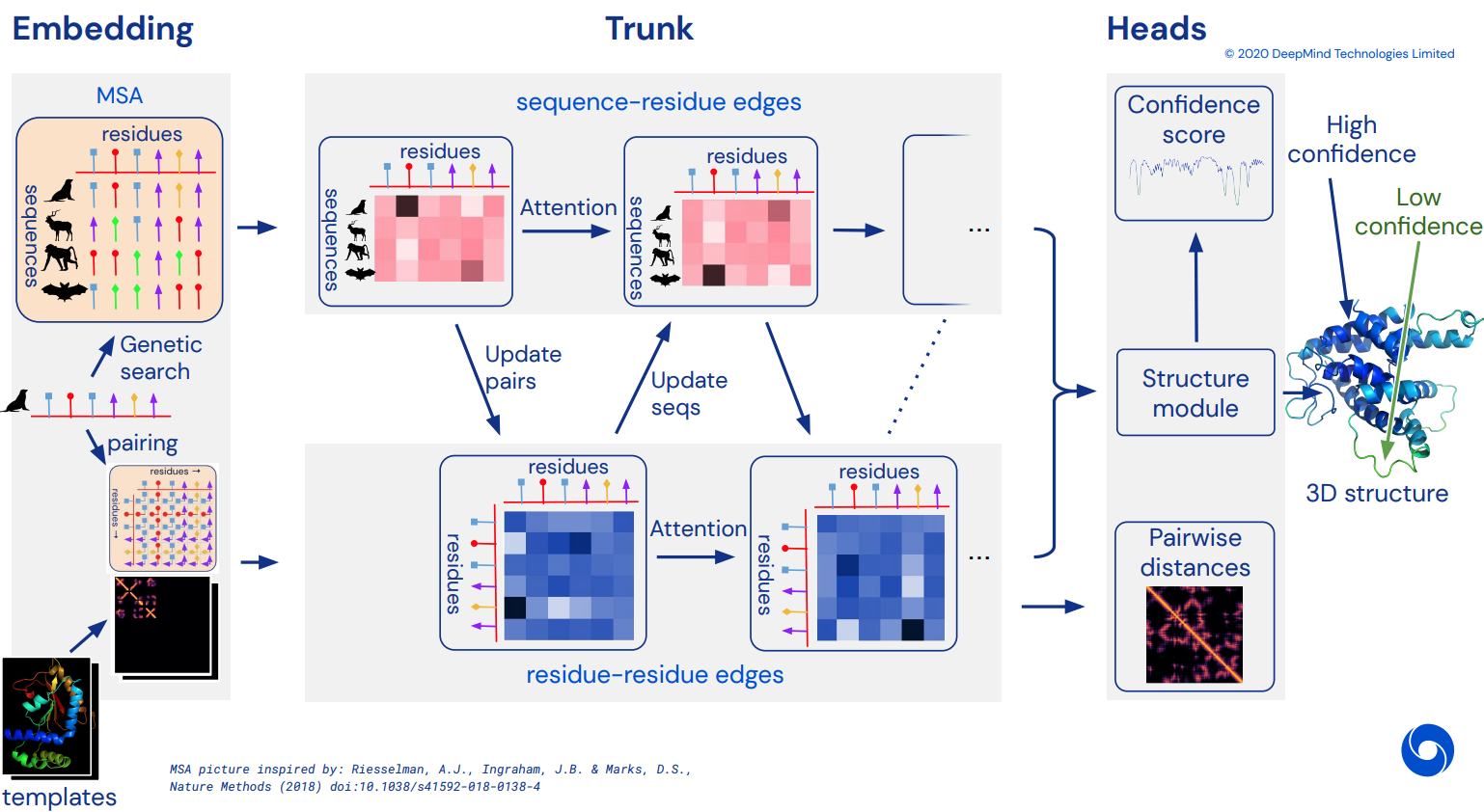
В конечном итоге стать неофициальной рабочей реализацией Pytorch Alphafold2, потрясающей сети внимания, которая решила CASP14. Будет постепенно реализовано по мере появления более подробной информации об архитектуре.
Как только это будет воспроизведено, я намерен сложить все доступные аминокислотные последовательности in silico и выпустить их как академический поток для дальнейшего развития науки. Если вы заинтересованы в усилиях по репликации, зайдите по хэштегу #alphafold на этом канале Discord.
Обновление: Deepmind открыл исходный код официального кода Jax вместе с весами! Этот репозиторий теперь будет ориентирован на прямой перевод Pytorch с некоторыми улучшениями в позиционном кодировании.
Видео ArxivInsights
$ pip install alphafold2-pytorchlhatsk сообщил об обучении модифицированного ствола этого репозитория с использованием той же настройки, что и trRosetta, с конкурентоспособными результатами.
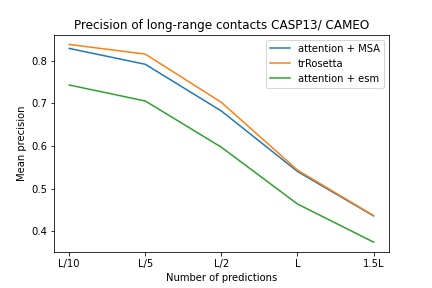
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk
Прогнозирование дистограммы, как у Alphafold-1, но с вниманием
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda () # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda () # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Вы также можете включить прогнозирование углов, передав predict_angles = True при инициализации. Приведенный ниже пример будет эквивалентен trRosetta, но с самостоятельным/перекрестным вниманием.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_angles = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram , theta , phi , omega = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25) В недавней статье Фабиана предлагается итеративная подача координат обратно в SE3 Transformer с разделением веса. Я решил реализовать эту идею, хотя вопрос о том, как она на самом деле работает, еще не решен.
Вы также можете использовать E(n)-Transformer или EGNN для структурного уточнения.
Обновление: лаборатория Бейкера показала, что сквозная архитектура от последовательностей и вложений MSA до SE3 Transformers может превзойти trRosetta и сократить разрыв с Alphafold2. Мы будем использовать преобразователь графов, который действует на встраивания магистралей, для генерации исходного набора координат для отправки в эквивариантную сеть. (Это дополнительно подтверждается Костой и др. в их работе по выявлению 3D-координат из вложений MSA Transformer в статье, предшествовавшей работе лаборатории Бейкера)
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
structure_module_type = 'se3' , # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
structure_module_dim = 4 , # se3 transformer dimension
structure_module_depth = 1 , # depth
structure_module_heads = 1 , # heads
structure_module_dim_head = 16 , # dimension of heads
structure_module_refinement_iters = 2 , # number of equivariant coordinate refinement iterations
structure_num_global_nodes = 1 # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Основное предположение заключается в том, что магистраль работает на уровне остатков, а затем достраивается до атомарного уровня для структурного модуля, будь то трансформаторы SE3, E(n)-трансформатор или EGNN, выполняющие уточнение. По умолчанию в этой библиотеке используются 3 атома основной цепи (C, Ca, N), но вы можете настроить ее для включения любого другого атома, который вам нравится, включая Cb и боковые цепи.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
atoms = 'backbone-with-cbeta'
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 4, 3) <-- 4 atoms per residue (C, Ca, N, Cb) Допустимые варианты для atoms включают:
backbone - 3 атома основной цепи (C, Ca, N) [по умолчанию]backbone-with-cbeta - 3 атома основной цепи и C бетаbackbone-with-oxygen - 3 атома основной цепи и кислород от карбоксилаbackbone-with-cbeta-and-oxygen - 3 атома основной цепи с C-бета и кислородомall — основная цепь и все остальные атомы из боковой цепиВы также можете передать тензор формы (14), определяющий, какие атомы вы хотите включить.
бывший.
atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])Этот репозиторий предлагает вам легко дополнить сеть предварительно обученными встраиваниями от Facebook AI. Он содержит оболочки для предварительно обученных ESM, MSA Transformers или Protein Transformer.
Есть некоторые предпосылки. Вам необходимо убедиться, что у вас установлена библиотека apex от Nvidia, поскольку предварительно обученные преобразователи используют некоторые объединенные операции.
Или вы можете попробовать запустить скрипт ниже
git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./ Далее вам просто нужно будет импортировать и обернуть экземпляр Alphafold2 с помощью ESMEmbedWrapper , MSAEmbedWrapper или ProtTranEmbedWrapper , и он позаботится о внедрении как последовательности, так и выравниваний нескольких последовательностей за вас (и проецировании его на размеры, указанные в вашем модель). Ничего не нужно менять, кроме добавления обертки.
import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64
)
model = MSAEmbedWrapper (
alphafold2 = alphafold2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) По умолчанию, даже если оболочка предоставляет магистральному каналу внедрения последовательности и MSA, они будут суммироваться с обычными внедрениями токенов. Если вы хотите обучать Alphafold2 без встраивания токенов (полагайтесь только на предварительно обученные встраивания), вам нужно будет установить для disable_token_embed значение True при инициализации Alphafold2 .
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
disable_token_embed = True
) В статье Цзиньбо Сюя предполагается, что не нужно группировать расстояния, а вместо этого можно напрямую прогнозировать среднее и стандартное отклонение. Вы можете использовать это, включив один флаг predict_real_value_distances , и в этом случае возвращаемый прогноз расстояния будет иметь размерность 2 для среднего и стандартного отклонения соответственно.
Если predict_coords также включен, то MDS будет принимать прогнозы среднего и стандартного отклонения напрямую, без необходимости вычислять их из ячеек дистограммы.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
predict_real_value_distances = True , # set this to True
structure_module_type = 'se3' ,
structure_module_dim = 4 ,
structure_module_depth = 1 ,
structure_module_heads = 1 ,
structure_module_dim_head = 16 ,
structure_module_refinement_iters = 2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Вы можете добавить сверточные блоки как для первичной последовательности, так и для MSA, просто установив один дополнительный аргумент ключевого слова use_conv = True
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37)Сверточные ядра следуют примеру этой статьи, объединяя ядра 1d и 2d в один блок, подобный resnet. Вы можете полностью настроить ядра как таковые.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Вы также можете выполнить расширение цикла с помощью одного дополнительного аргумента ключевого слова. Расширение по умолчанию равно 1 для всех слоев.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Наконец, вместо того, чтобы следовать шаблону извилин, самообслуживания и перекрестного внимания на глубину, вы можете настроить любой порядок, который пожелаете, с помощью ключевого слова custom_block_types
бывший. Сеть, в которой вы сначала выполняете преимущественно свертки, а затем блоки внимания на себя + перекрестного внимания.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
heads = 8 ,
dim_head = 64 ,
custom_block_types = (
* (( 'conv' ,) * 6 ),
* (( 'self' , 'cross' ) * 6 )
)
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Вы можете тренироваться с помощью Sparse Attention от Microsoft Deepspeed, но вам придется потерпеть процесс установки. Это два шага.
Сначала вам необходимо установить Deepspeed с Sparse Attention.
$ sh install_deepspeed.sh Далее вам необходимо установить пакет pip triton
$ pip install tritonЕсли оба вышеперечисленных пункта удались, теперь вы можете тренироваться с «Разреженным вниманием»!
К сожалению, скудное внимание поддерживается только за счет собственного внимания, а не перекрестного внимания. Я предложу другое решение для повышения эффективности перекрестного внимания.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
max_seq_len = 2048 , # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = ( True , False ) * 6 # interleave sparse and full attention for all 12 layers
). cuda ()Я также добавил один из лучших вариантов линейного внимания в надежде уменьшить бремя перекрестного присутствия. Лично я не нашел, чтобы Performer работал так хорошо, но, поскольку в статье они сообщали некоторые хорошие цифры для тестов белка, я решил включить его и позволить другим экспериментировать.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()Вы также можете указать точные слои, для которых вы хотите использовать линейное внимание, передав кортеж той же длины, что и глубина.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()В этом документе предполагается, что если у вас есть запросы или контексты, которые имеют определенные оси (например, изображение), вы можете уменьшить количество необходимого внимания, усредняя значения по этим осям (высоте и ширине) и объединяя усредненные оси в одну последовательность. Вы можете включить это как метод экономии памяти для перекрестного внимания, особенно для основной последовательности.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda () Вы также можете применить тот же оператор к MSA во время перекрестного внимания с помощью флага cross_attn_kron_msa , если ваши MSA выровнены и имеют одинаковую ширину.
Тодо
Чтобы сэкономить память на перекрестное внимание, вы можете установить степень сжатия ключа/значений, следуя схеме, изложенной в этой статье. Обычно приемлема степень сжатия 2-4.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_compress_ratio = 3
). cuda ()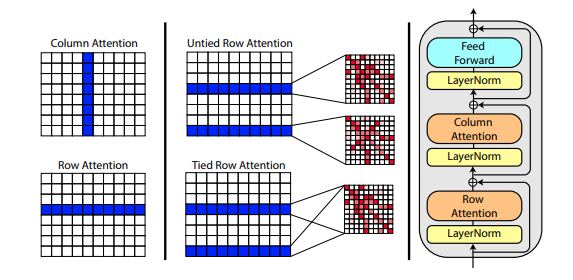
В новой статье Рошана Рао предлагается использовать осевое внимание для предварительной тренировки MSA. Учитывая хорошие результаты, этот репозиторий будет использовать ту же схему в магистрали, специально для самообслуживания MSA.
Вы также можете связать внимание к строкам MSA с настройкой msa_tie_row_attn = True при инициализации Alphafold2 . Однако, чтобы использовать это, вы должны убедиться, что если у вас нечетное количество MSA на первичную последовательность, маска MSA правильно установлена на False для неиспользуемых строк.
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
msa_tie_row_attn = True # just set this to true
)Обработка шаблонов также в основном осуществляется с осевым вниманием, а перекрестное внимание осуществляется по количеству измерений шаблона. Во многом это следует той же схеме, что и в недавнем подходе к классификации видео с концентрацией внимания, как показано здесь.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_coors = templates_coors ,
templates_mask = templates_mask
)Если также присутствует информация о боковой цепи в виде единичного вектора между координатами C и C-альфа каждого остатка, вы также можете передать ее следующим образом.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_mask = templates_mask ,
templates_coors = templates_coors ,
templates_sidechains = templates_sidechains
)Я подготовил повторную реализацию SE3 Transformer, как объяснил Фабиан Фукс в спекулятивном блоге.
Кроме того, в новой статье Виктора и Веллинга используются инвариантные функции для E(n)-эквивариантности, что позволяет достичь SOTA и превосходить SE3 Transformer в ряде тестов, при этом работая намного быстрее. Я взял основные идеи из этой статьи и изменил ее, чтобы она стала преобразователем (добавил внимание как функциям, так и обновлениям координат).
Все три приведенные выше эквивариантные сети интегрированы и доступны для использования в репозитории для уточнения атомарных координат путем простой установки одного гиперпараметра structure_module_type .
se3 SE3 Трансформатор
egnn ЕГНН
en E(n)-Трансформатор
Представляет интерес для читателей тот факт, что каждая из трех структур также была проверена исследователями по смежным проблемам.
$ python setup.py test Эта библиотека будет использовать потрясающую работу Джонатана Кинга из этого репозитория. Спасибо, Джонатан!
У нас также есть данные MSA, все объемом около 3,5 ТБ, загруженные и размещенные Archivist, которому принадлежит проект The-Eye. (Они также размещают данные и модели для Eleuther AI). Пожалуйста, рассмотрите возможность пожертвования, если вы найдете их полезными.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-ones-child-has-left-home/

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
Презентация tFold от лаборатории искусственного интеллекта Tencent
cd downloads_folder > pip install pyrosetta_wheel_filename.whlOpenMM Янтарный
@misc { unpublished2021alphafold2 ,
title = { Alphafold2 } ,
author = { John Jumper } ,
year = { 2020 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @article { Rao2021.02.12.430858 ,
author = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
title = { MSA Transformer } ,
year = { 2021 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
journal = { bioRxiv }
} @article { Rives622803 ,
author = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
title = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
year = { 2019 } ,
doi = { 10.1101/622803 } ,
publisher = { Cold Spring Harbor Laboratory } ,
journal = { bioRxiv }
} @article { Elnaggar2020.07.12.199554 ,
author = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
title = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
elocation-id = { 2020.07.12.199554 } ,
year = { 2021 } ,
doi = { 10.1101/2020.07.12.199554 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
journal = { bioRxiv }
} @misc { king2020sidechainnet ,
title = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } ,
author = { Jonathan E. King and David Ryan Koes } ,
year = { 2020 } ,
eprint = { 2010.08162 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { alquraishi2019proteinnet ,
title = { ProteinNet: a standardized data set for machine learning of protein structure } ,
author = { Mohammed AlQuraishi } ,
year = { 2019 } ,
eprint = { 1902.00249 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { fuchs2021iterative ,
title = { Iterative SE(3)-Transformers } ,
author = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
year = { 2021 } ,
eprint = { 2102.13419 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { su2021roformer ,
title = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
author = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
year = { 2021 } ,
eprint = { 2104.09864 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CL }
} @article { Gao_2020 ,
title = { Kronecker Attention Networks } ,
ISBN = { 9781450379984 } ,
url = { http://dx.doi.org/10.1145/3394486.3403065 } ,
DOI = { 10.1145/3394486.3403065 } ,
journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
publisher = { ACM } ,
author = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
year = { 2020 } ,
month = { Jul }
} @article { Si2021.05.10.443415 ,
author = { Si, Yunda and Yan, Chengfei } ,
title = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
elocation-id = { 2021.05.10.443415 } ,
year = { 2021 } ,
doi = { 10.1101/2021.05.10.443415 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
journal = { bioRxiv }
} @article { Costa2021.06.02.446809 ,
author = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
title = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.02.446809 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
journal = { bioRxiv }
} @article { Baek2021.06.14.448402 ,
author = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
title = { Accurate prediction of protein structures and interactions using a 3-track network } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.14.448402 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
journal = { bioRxiv }
}