@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Знаете ли вы, что Neurodiffeq поддерживает пакеты решений и может использоваться для решения обратных задач? Смотрите здесь!
? Уже знакомы с нейродиффеком? ? Перейти к часто задаваемым вопросам.
neurodiffeq — пакет для решения дифференциальных уравнений с помощью нейронных сетей. Дифференциальные уравнения – это уравнения, связывающие некоторую функцию с ее производными. Они возникают в различных научных и инженерных областях. Традиционно эти проблемы можно решить численными методами (например, метод конечных разностей, метод конечных элементов). Хотя эти методы эффективны и адекватны, их выразимость ограничена представлением их функций. Было бы интересно, если бы мы могли вычислить решения для дифференциальных уравнений, которые были бы непрерывными и дифференцируемыми.
Было показано, что в качестве аппроксиматоров универсальных функций искусственные нейронные сети обладают потенциалом для решения обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных (УЧП) с определенными начальными/граничными условиями. Цель neurodiffeq — реализовать существующие методы использования ИНС для решения дифференциальных уравнений таким образом, чтобы программное обеспечение было достаточно гибким для работы над широким спектром задач, определяемых пользователем.
Как и большинство стандартных библиотек, neurodiffeq размещается на PyPI. Чтобы установить последнюю стабильную версию,
pip install -U neodiffeq # '-U' означает обновление до последней версии
Кроме того, вы можете установить библиотеку вручную, чтобы получить ранний доступ к нашим новым функциям. Это рекомендуемый способ для разработчиков, которые хотят внести свой вклад в библиотеку.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd нейродиффек && pip install -r требования установка пипа. # Чтобы внести изменения в библиотеку, используйте `pip install -e .`pytesttests/ # Запустите тесты. Необязательный.
Мы рады помочь вам с любыми вопросами. А пока вы можете ознакомиться с часто задаваемыми вопросами.
Чтобы просмотреть полные руководства и документацию по neurodiffeq , посетите официальную документацию.
В дополнение к документации мы недавно сделали краткое демонстрационное видео со слайдами.
из Neurodiffeq импортировать diffиз Neurodiffeq.solvers импорт Solver1D, Solver2Dиз Neurodiffeq.conditions импортировать IVP, DirichletBVP2Dиз Neurodiffeq.networks импортировать FCNN, SinActv
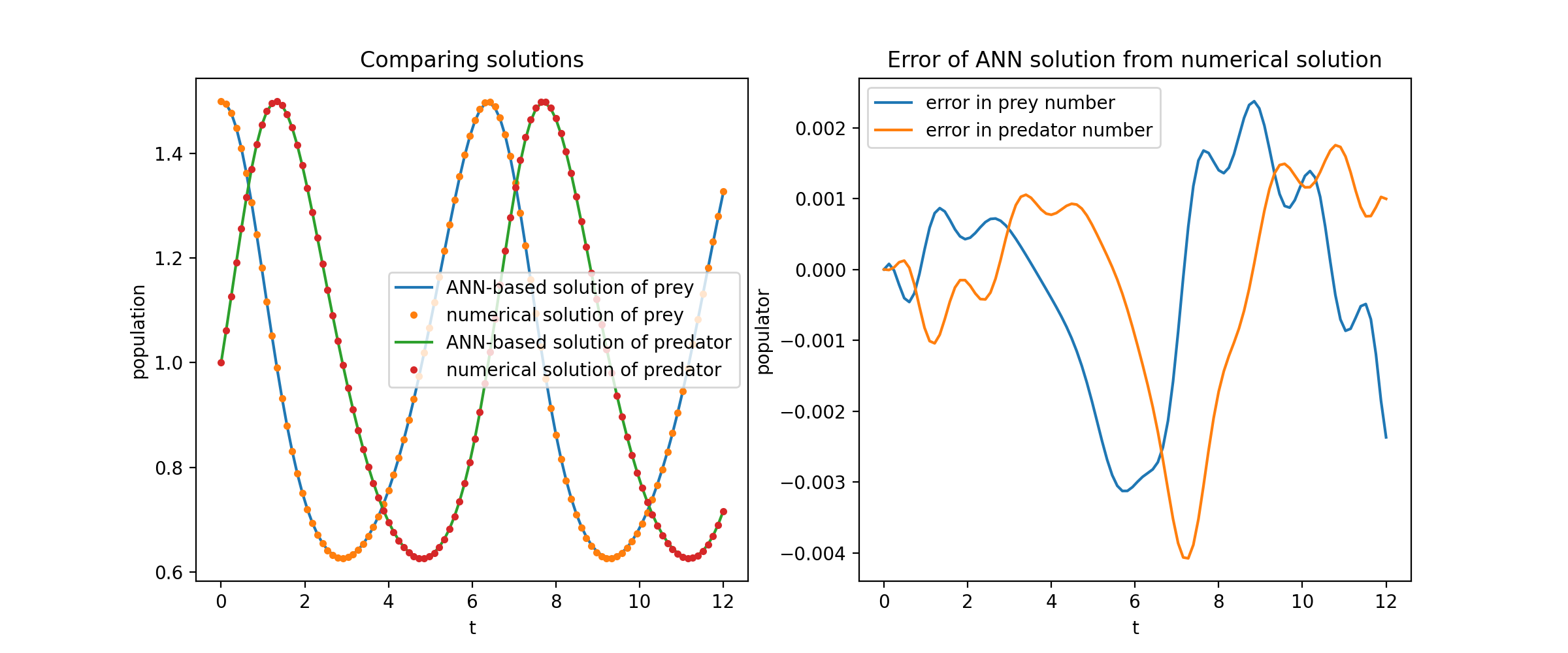
Здесь мы решаем нелинейную систему двух ОДУ, известную как уравнения Лотки–Вольтерра. Есть две неизвестные функции ( u и v ) и одна независимая переменная ( t ).
def ode_system(u, v, t): вернуть [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]условия = [IVP(t_0=0.0, u_0=1.5) ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, условия, t_min=0,1, t_max=12,0, nets=nets)solver.fit(max_epochs=3000)solution =solver.get_solution()
solution - это вызываемый объект, вы можете передать ему массивы numpy или тензоры факелов, например
u, v = Solution(t, to_numpy=True) # t может быть np.ndarray или torch.Tensor
Сопоставление графиков u и v с их аналитическими решениями дает что-то вроде:
Здесь мы решаем уравнение Лапласа с граничными условиями Дирихле на прямоугольнике. Обратите внимание, что мы выбрали уравнение Лапласа из-за простоты его аналитического решения. На практике вы можете попробовать использовать любые нелинейные, хаотические УЧП , при условии, что вы достаточно хорошо настроили решатель.
Решение двумерной системы УЧП очень похоже на решение ОДУ, за исключением того, что есть две переменные x и y для краевых задач или x и t для начально-краевых задач, обе из которых поддерживаются.
def pde_system(u, x, y): return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: torch. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=лямбда x: 0, y_max=1, y_max_val=лямбда x: 0,
)
]nets = [FCNN(n_input_units=2, n_output_units=1, скрытые_юниты=(512,))]solver = Solver2D(pde_system, условия, xy_min=(0, 0), xy_max=(1, 1), nets=nets) Solver.fit(max_epochs=2000)solution =solver.get_solution() Сигнатура solution для 2D УЧП немного отличается от сигнатуры ОДУ. Опять же, он принимает либо массивы numpy, либо тензоры факелов.
u = решение (x, y, to_numpy = True)
Оценка u на [0,1] × [0,1] дает следующие графики
| Решение на основе ИНС | Остаток ПДЭ |
|---|---|
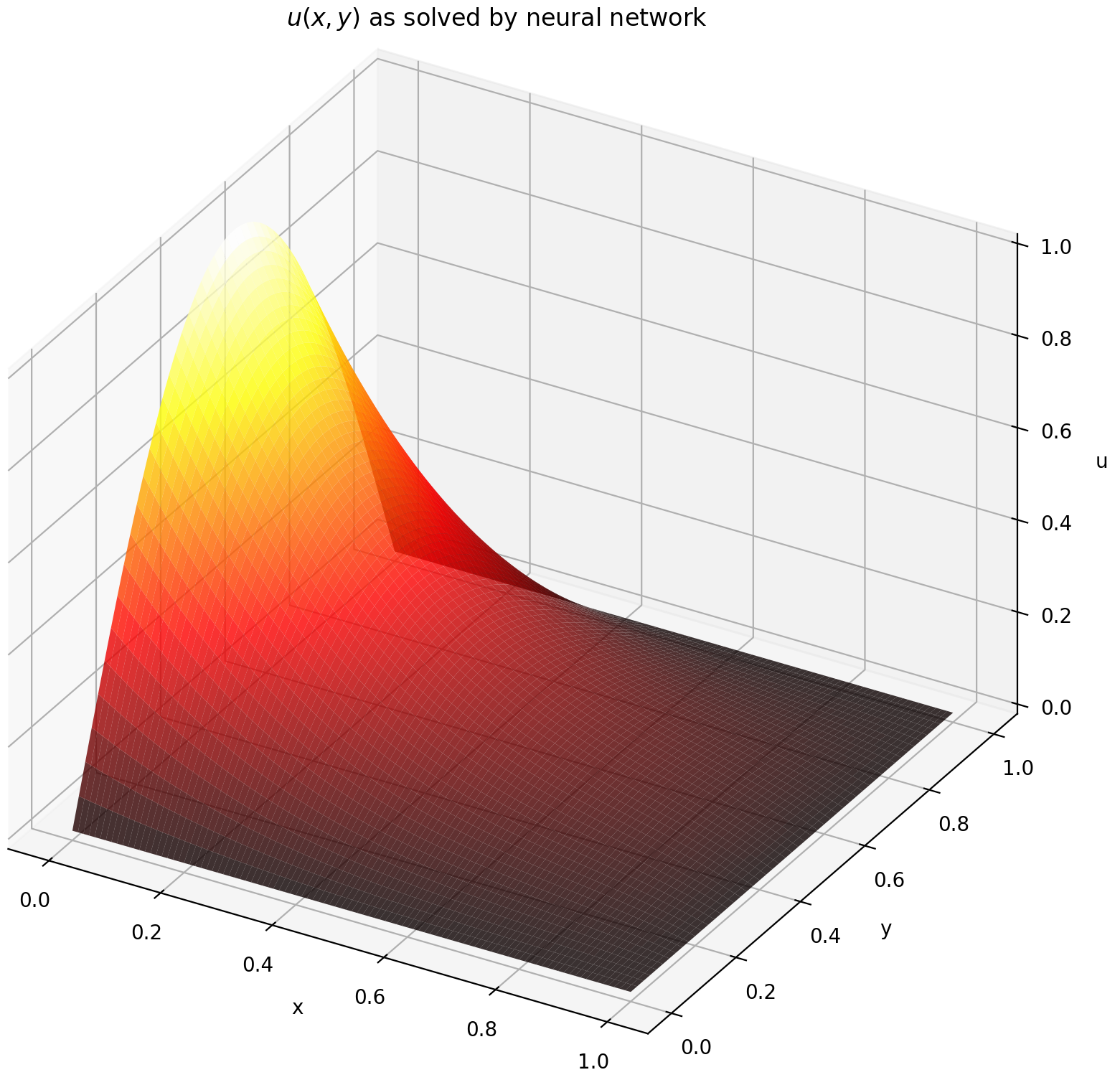 | 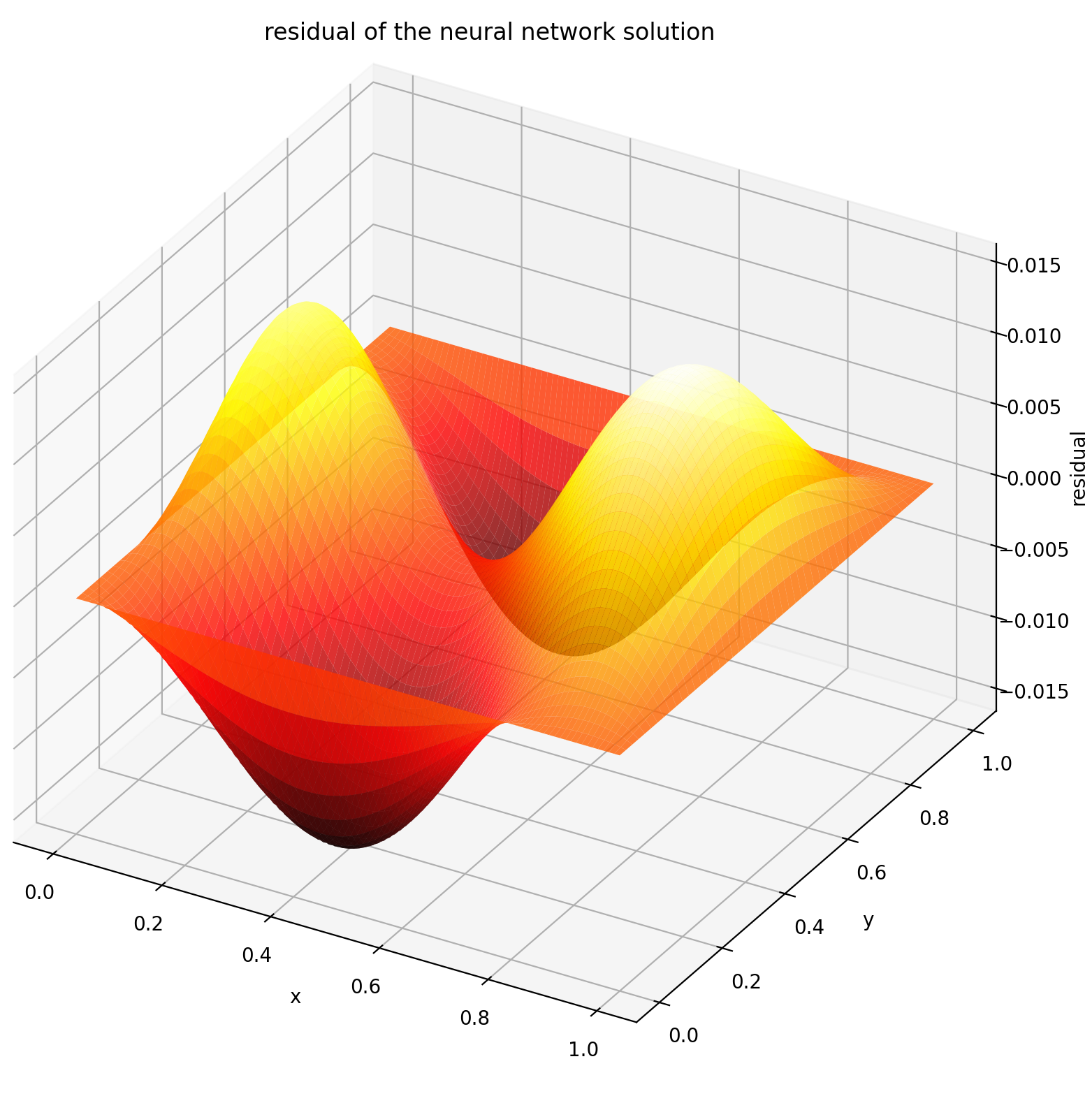 |
Монитор — это инструмент для визуализации решений PDE/ODE, а также истории потерь и пользовательских метрик во время обучения. Пользователям Jupyter Notebooks необходимо запустить волшебство %matplotlib notebook . Для пользователей Jupyter Lab попробуйте %matplotlib widget .
из Neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
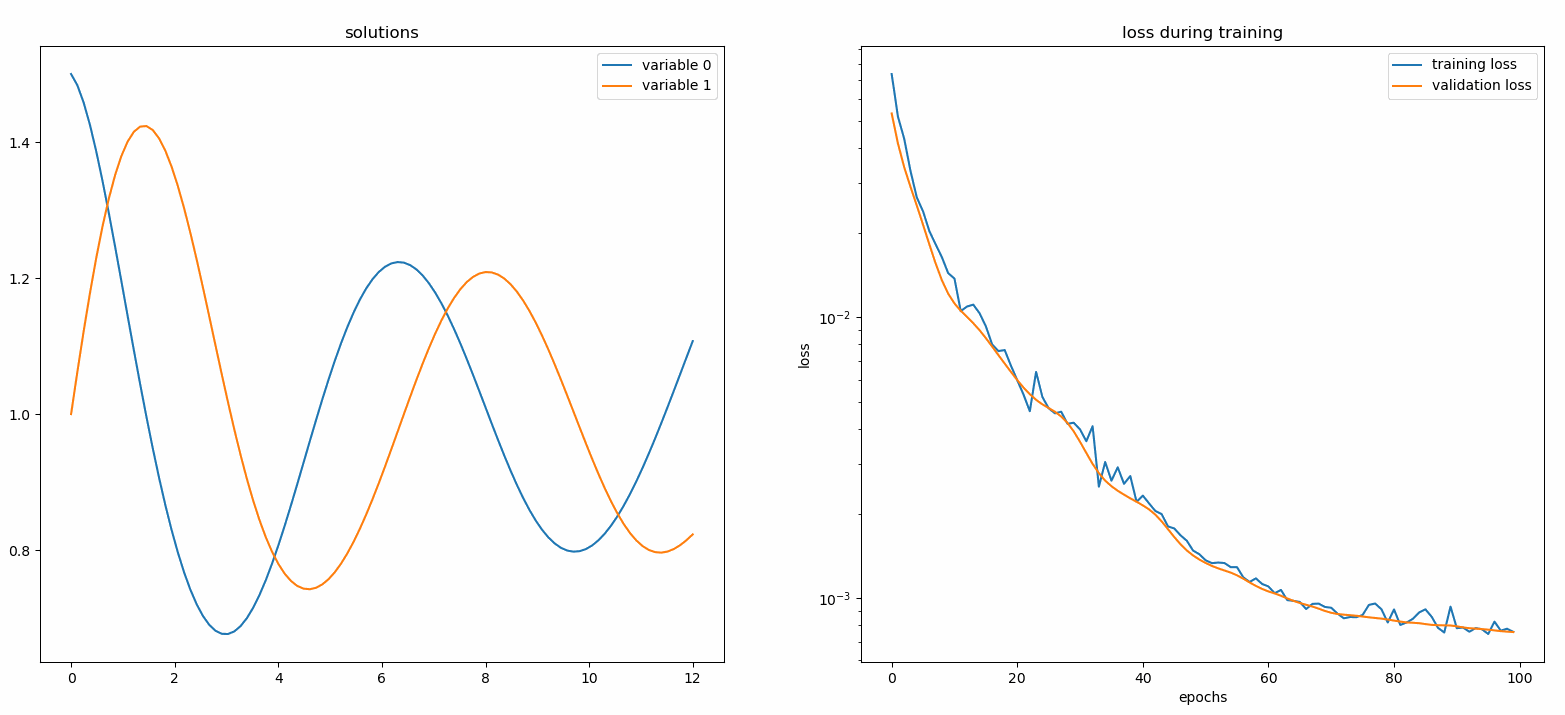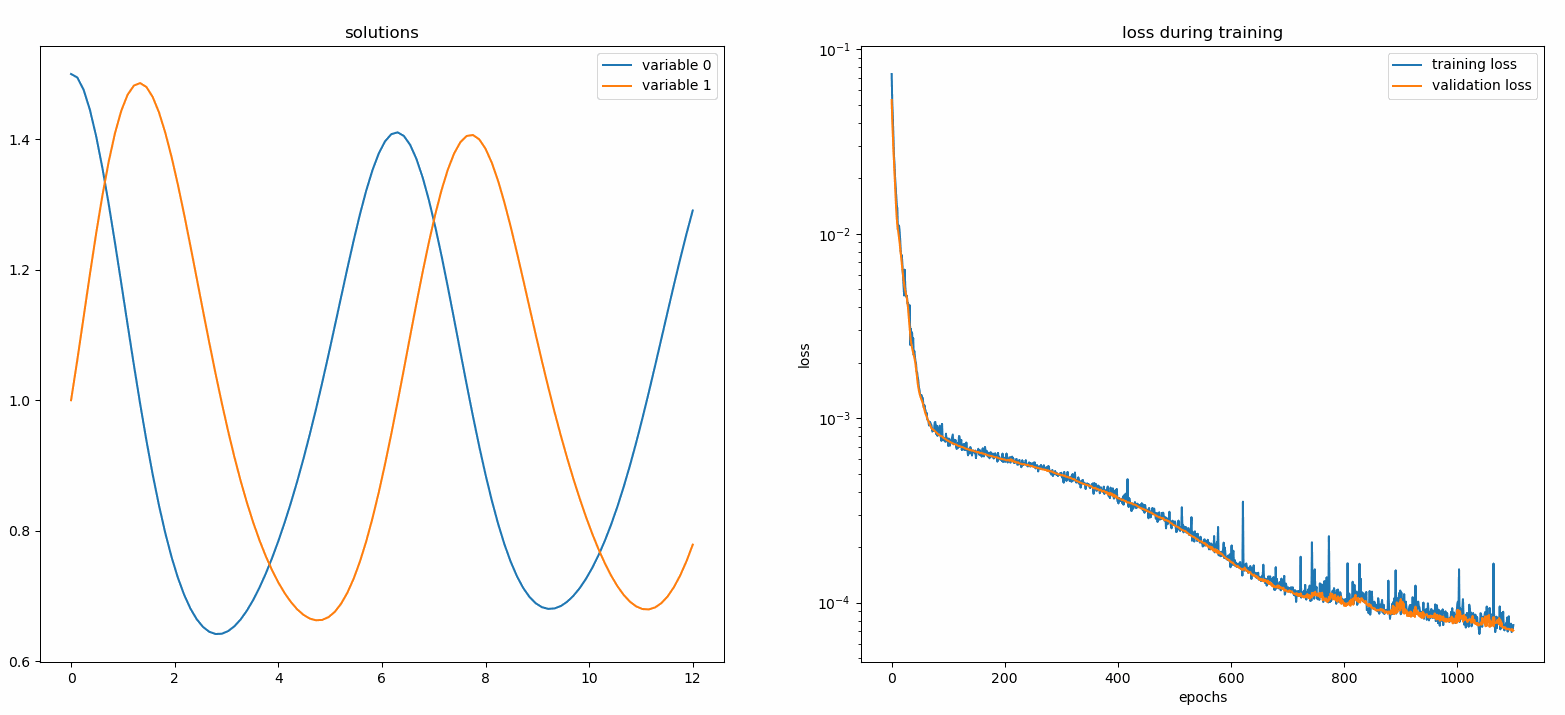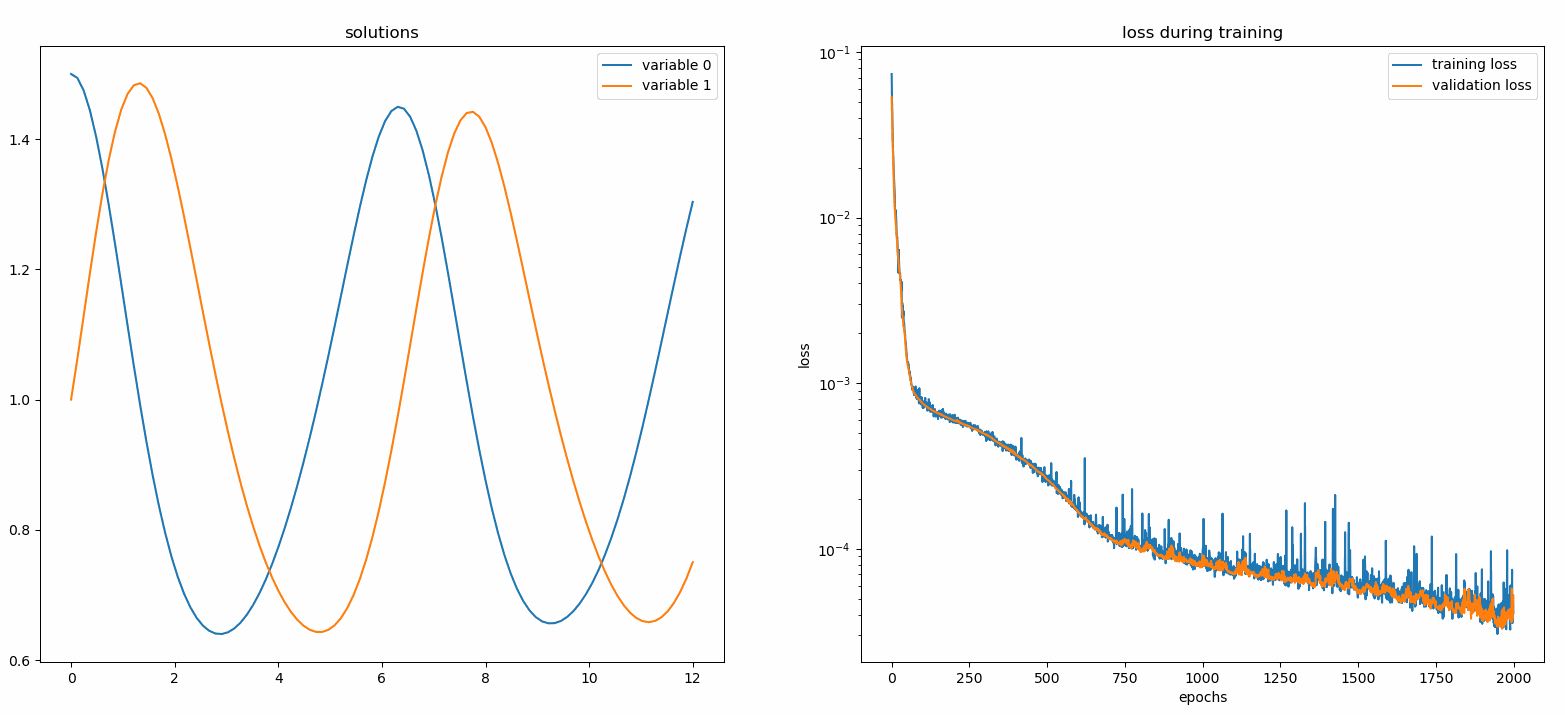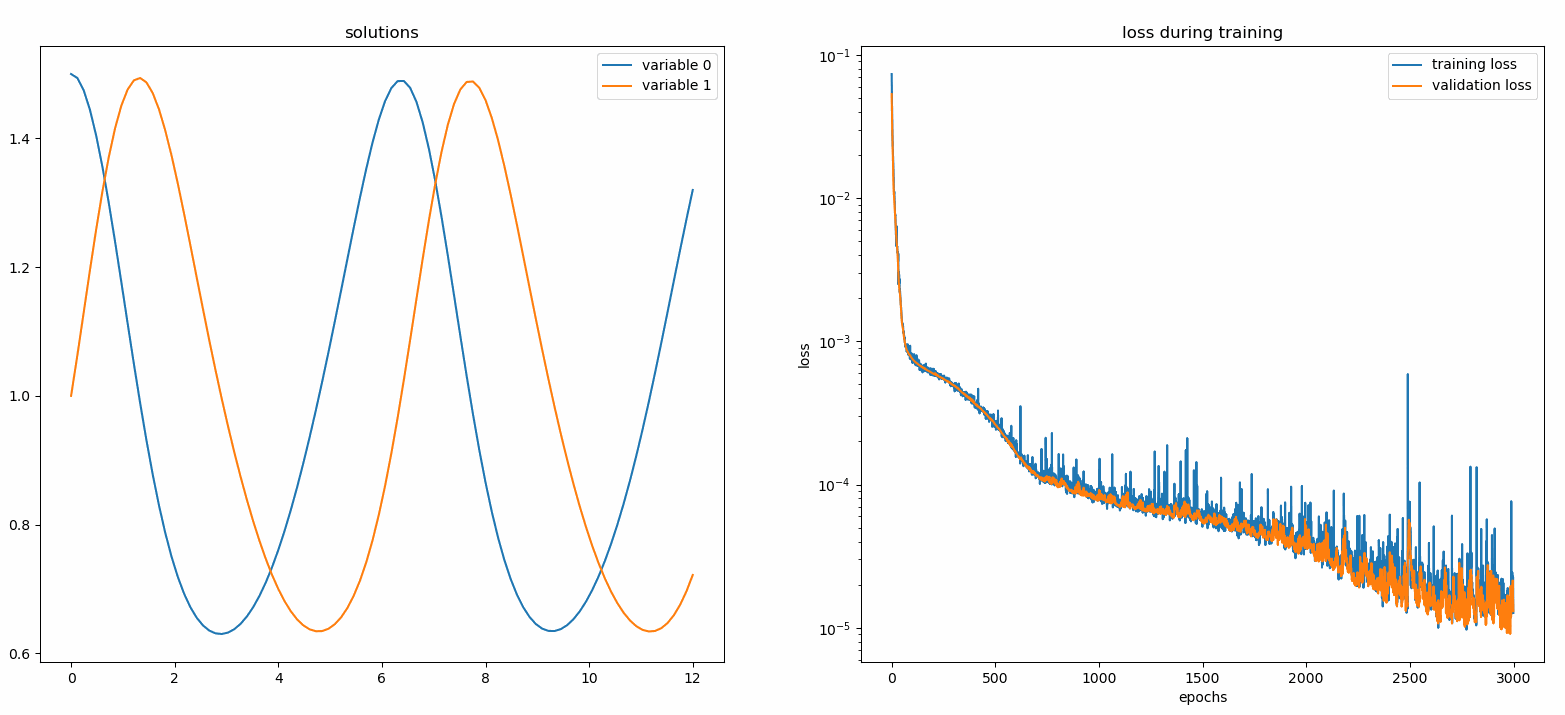
Вы должны увидеть, что графики обновляются каждые 100 эпох , а также в последнюю эпоху , показывая два графика — один для визуализации решения на интервале [0,12] , а другой для истории потерь (обучение и проверка).
Для удобства мы реализовали FCNN — полносвязную нейронную сеть, скрытые блоки и функции активации которой можно настраивать.
из Neurodiffeq.networks import FCNN# По умолчанию: n_input_units=1, n_output_units=1, Hidden_units=[32, 32], активация=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., Hidden_units=[ ..., ..., ...], активация=...) ...сети = [сеть1, сеть2, ...]
FCNN обычно является хорошей отправной точкой. Для опытных пользователей решатели совместимы с любым пользовательским torch.nn.Module . Единственными ограничениями являются:
Модули принимают тензор формы (None, n_coords) и выводят тензор формы (None, 1) .
Всего в nets должно быть n_funcs модулей, которые будут переданы в solver = Solver(..., nets=nets) .
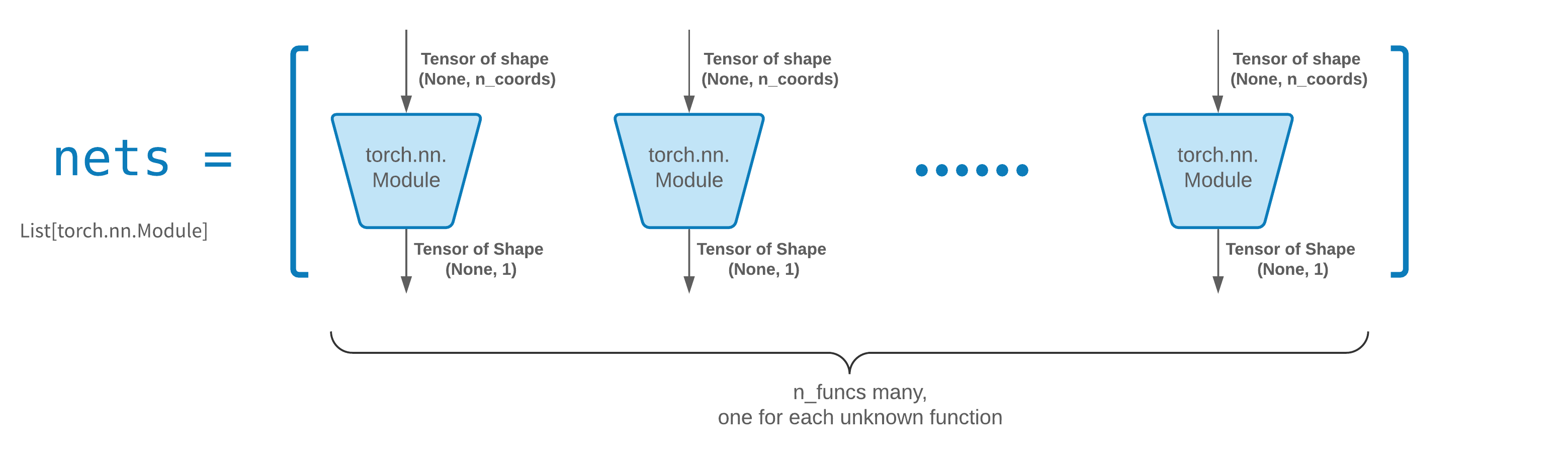
На самом деле, neurodiffeq есть функция Single_net , которая не подчиняется вышеуказанным правилам и не будет здесь рассматриваться.
Прочтите руководство по PyTorch по созданию собственной сетевой (модульной) архитектуры.
Перенос обучения легко выполнить, сериализовав old_solver.nets (список модулей Torch) на диск, а затем загрузив их и передав новому решателю:
old_solver.fit(max_epochs=...)# ... дамп `old_solver.nets` на диск# ... загрузить сети с диска, сохранить их в некоторой переменной `loaded_nets`new_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
В настоящее время мы работаем над функциями-оболочками для сохранения/загрузки сетей и других внутренних переменных решателей. А пока вы можете прочитать руководство PyTorch по сохранению и загрузке сетей.
В нейродиффеке сети обучаются путем минимизации потерь (остатков ODE/PDE), оцениваемых по набору точек в домене. Точки каждый раз пересчитываются случайным образом. Чтобы контролировать количество, распределение и ограничивающую область точек выборки, вы можете указать свои собственные generator обучения/проверки.
из Neurodiffeq.generators import Generator1D# По умолчанию t_min=0.0, t_max=1.0, метод='uniform', Noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., метод=.. ., Noise_std=...)g2 = Generator1D(size=..., t_min=..., t_max=..., метод=..., Noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
Вот несколько примеров дистрибутивов Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
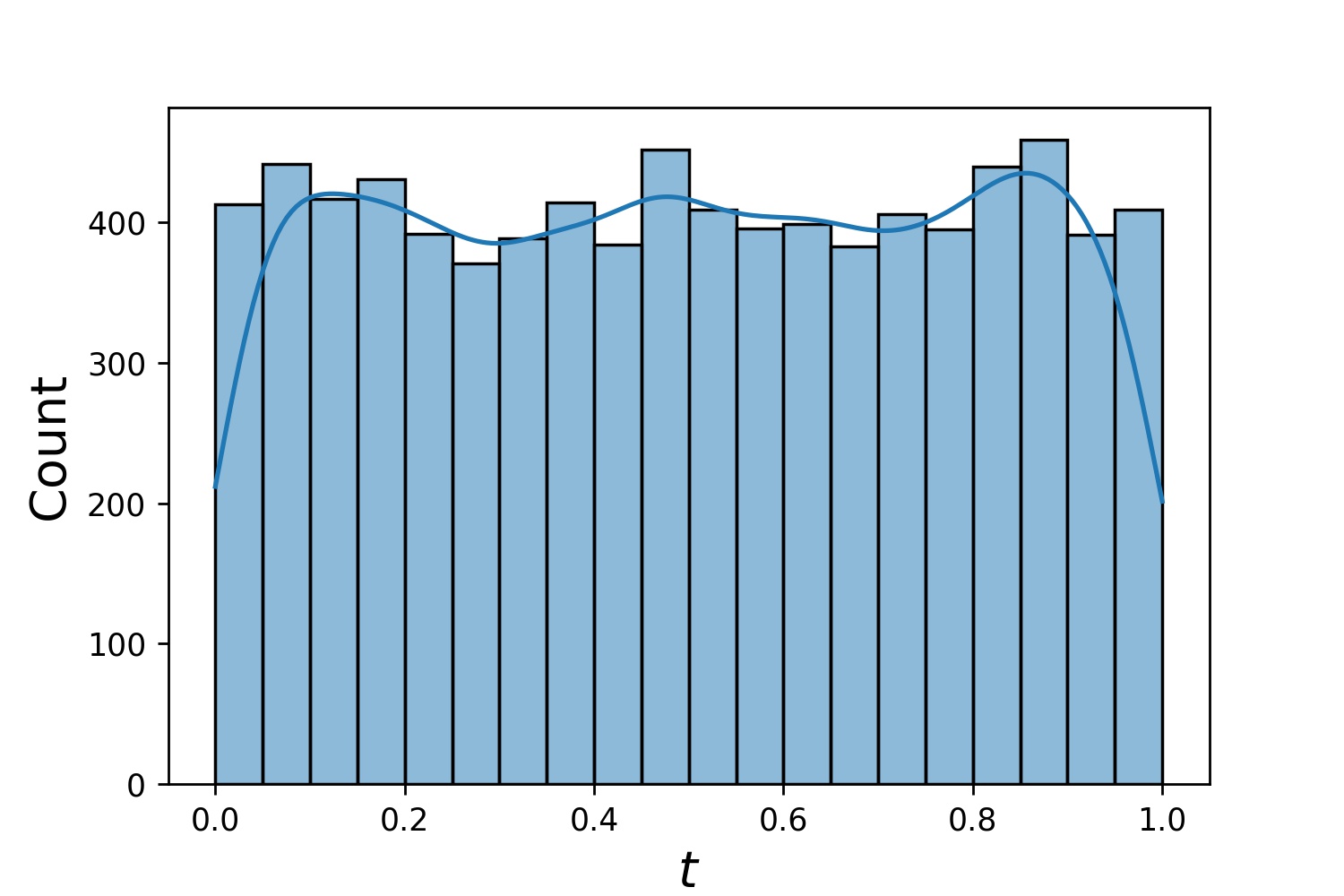 | 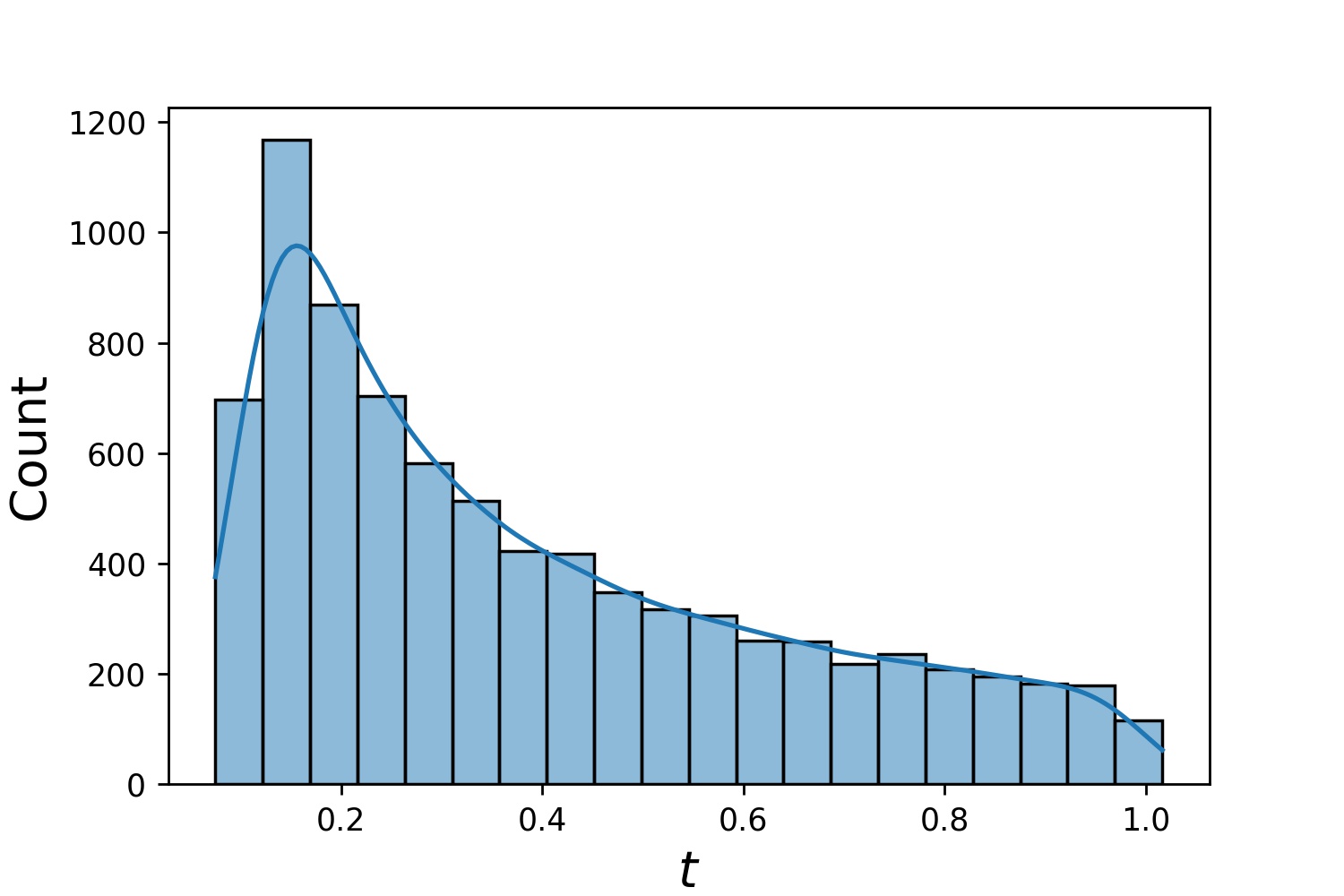 |
Обратите внимание: если указаны и train_generator , и valid_generator , t_min и t_max можно опустить в Solver1D(...) . Фактически, даже если вы передадите t_min , t_max , train_generator , valid_generator вместе, t_min и t_max все равно будут игнорироваться.
Еще одной приятной особенностью генераторов является то, что их можно объединять, например
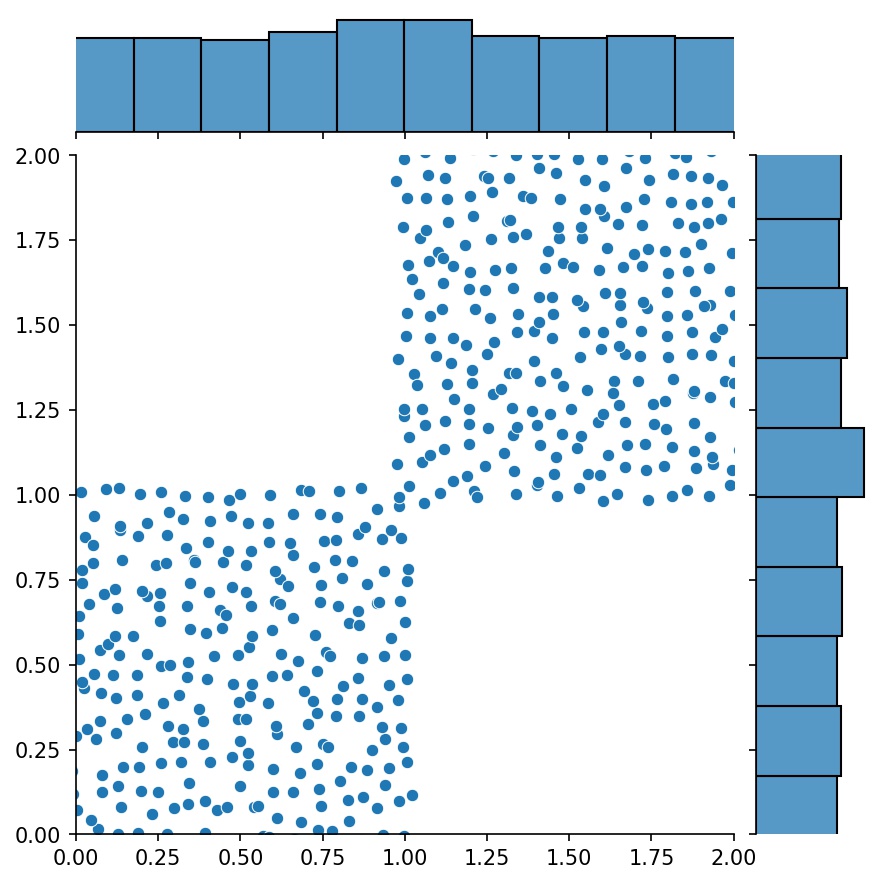
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2) ))g = g1 + g2
Здесь g будет генератором, который выводит объединенные выборки g1 и g2
g1 | g2 | g1 + g2 |
|---|---|---|
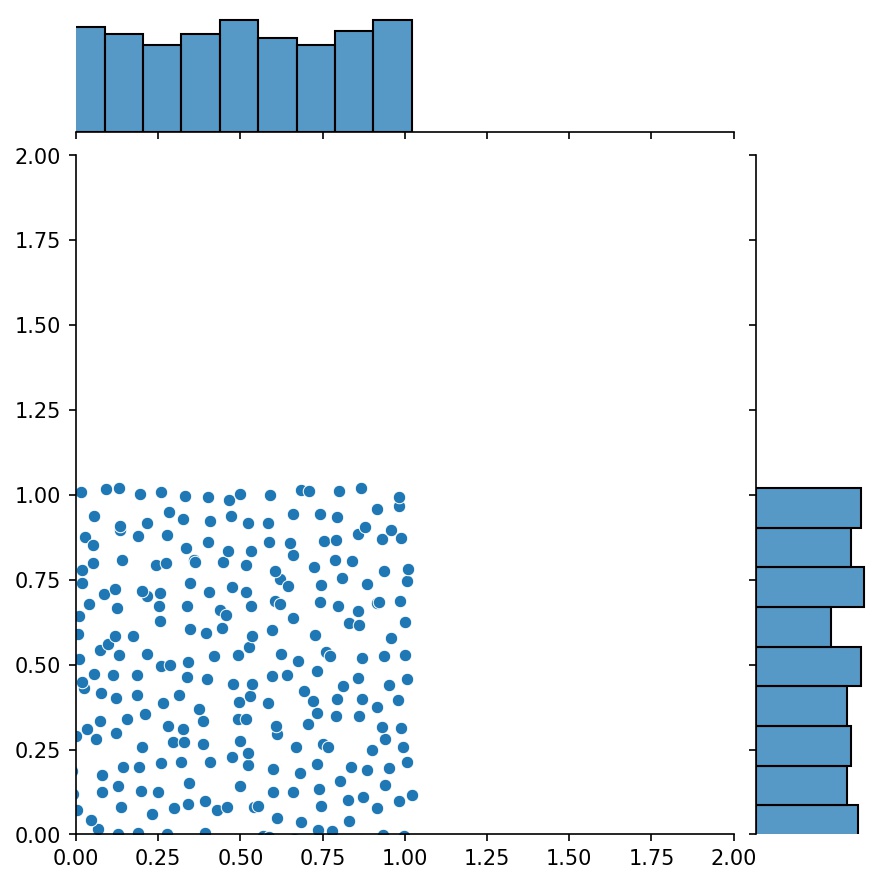 | 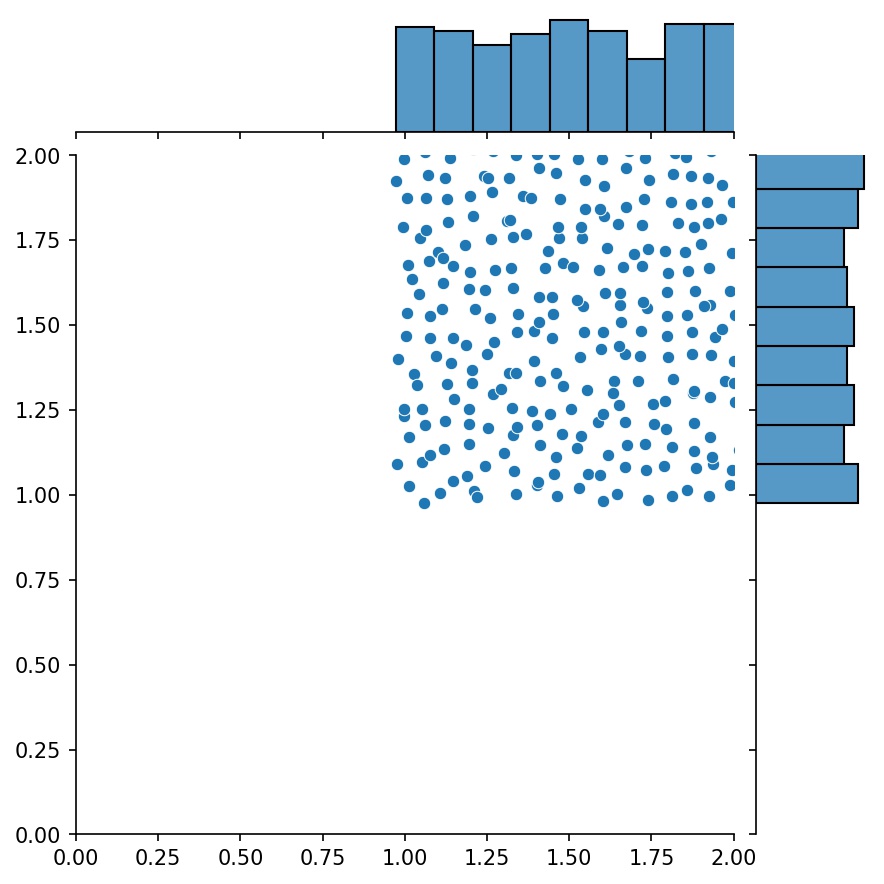 |  |
Вы можете использовать Generator2D , Generator3D и т. д. для точек выборки в более высоких измерениях. Но есть и другой способ
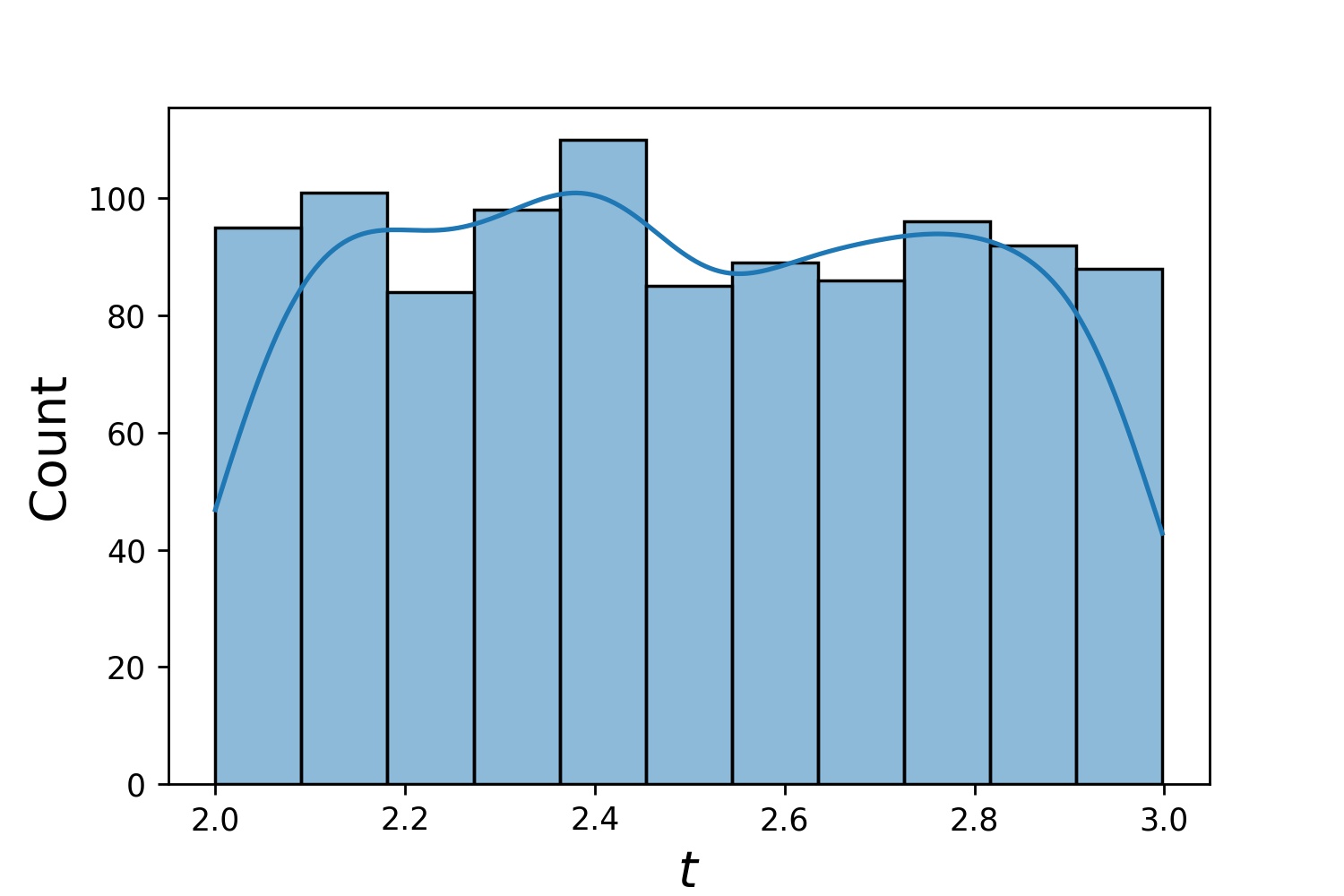
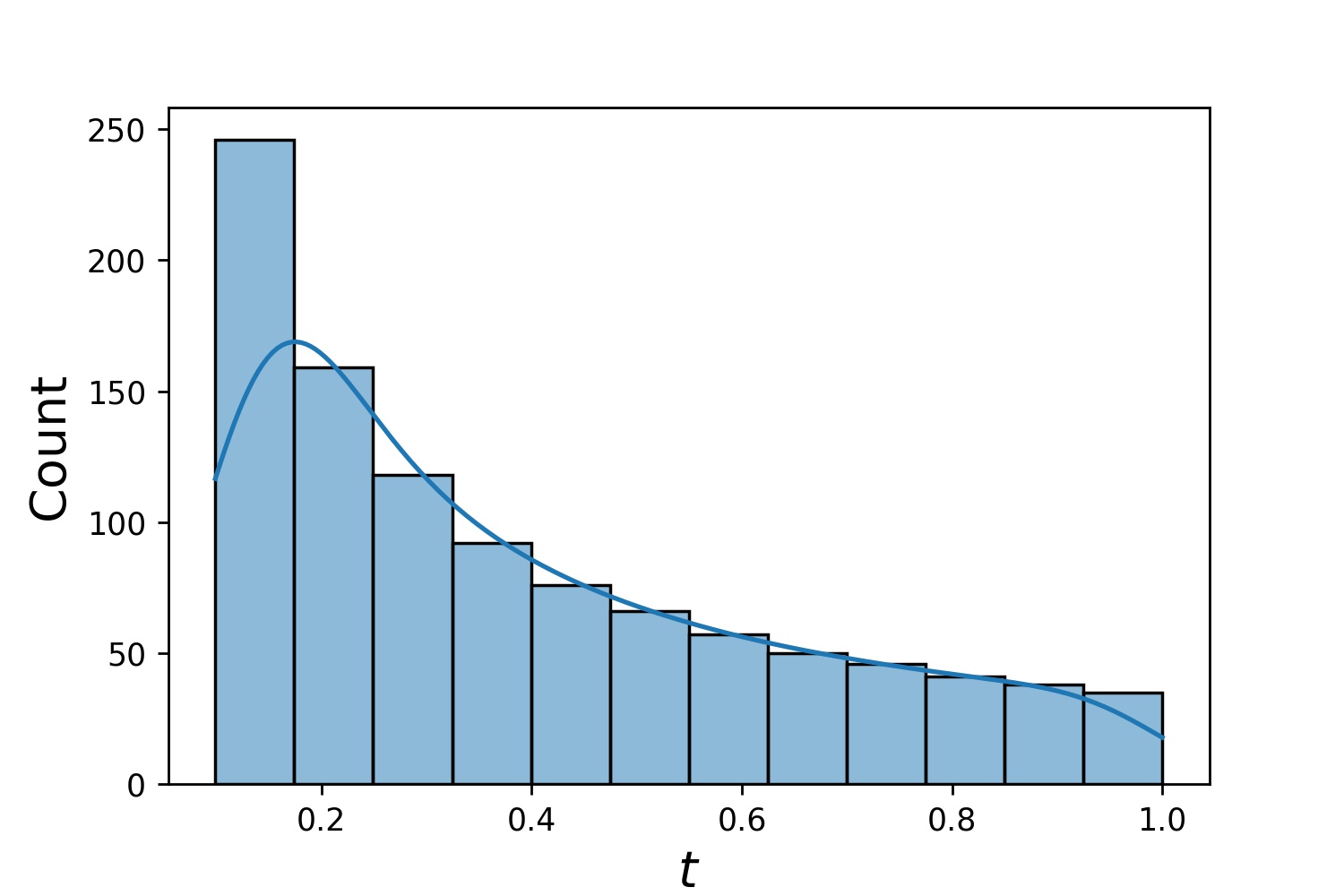
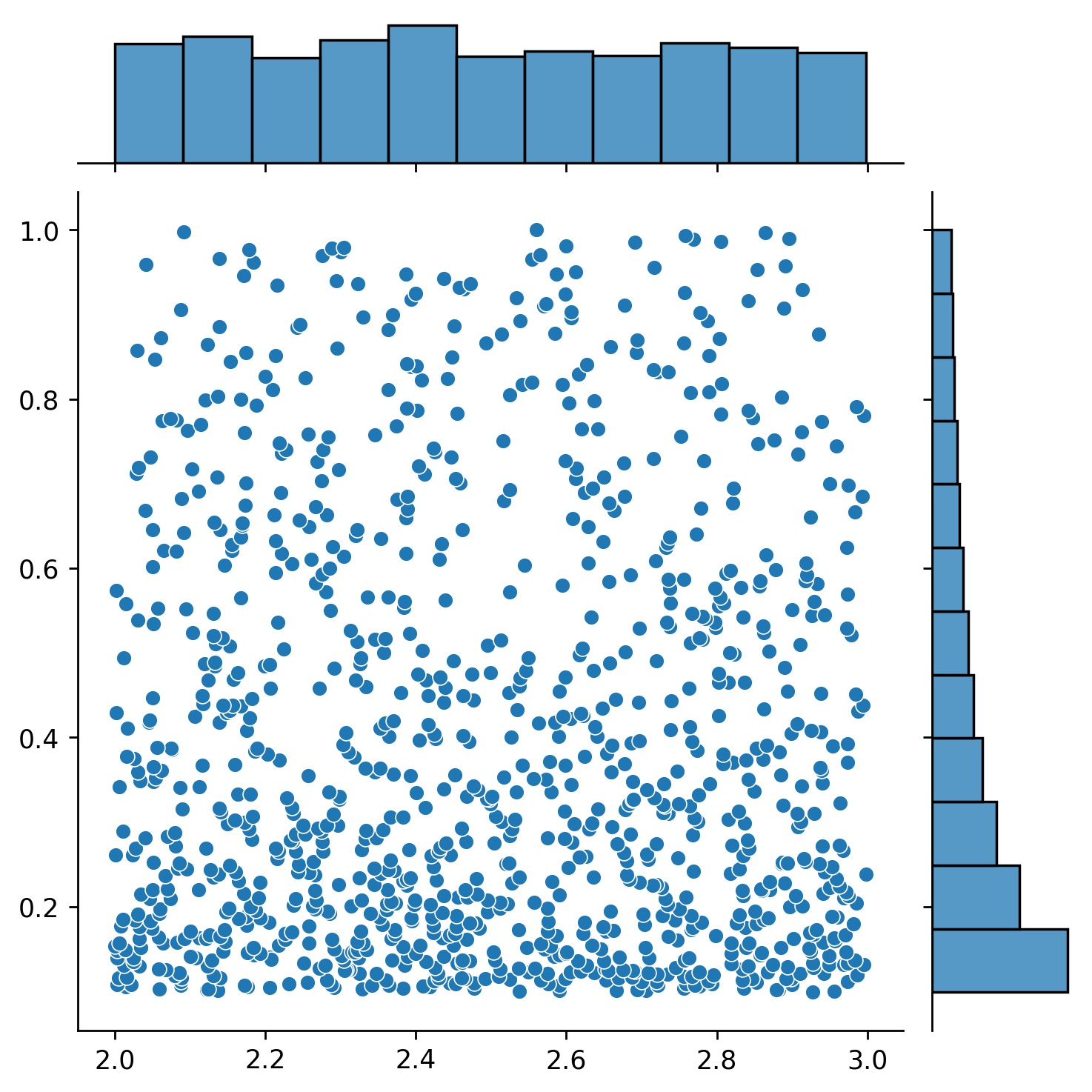
g1 = Generator1D(1024, 2.0, 3.0, метод='uniform')g2 = Generator1D(1024, 0.1, 1.0, метод='log-spaced-noisy', Noise_std=0.001)g = g1 * g2
Здесь g будет генератором, который каждый раз выдает 1024 точки в двумерном прямоугольнике (2,3) × (0.1,1) . Их координаты x извлекаются из (2,3) с использованием стратегии uniform , а координата y — из (0.1,1) с использованием стратегии log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
 |  |  |
Иногда интересно решить сразу несколько уравнений. Например, вы можете решить дифференциальные уравнения вида du/dt + λu = 0 при начальном условии u(0) = U0 . Возможно, вы захотите решить эту задачу для всех λ и U0 одновременно, рассматривая их как входные данные для нейронных сетей.
Одним из таких приложений являются химические реакции, скорость реакции которых неизвестна. Разные скорости реакций соответствуют разным растворам, и только одно решение соответствует наблюдаемым точкам данных. Возможно, вас заинтересует сначала найти набор решений, а затем определить наилучшие скорости реакции (то есть параметры уравнения). Второй шаг известен как обратная задача .
Вот пример того, как это сделать с помощью neurodiffeq :
Допустим, у нас есть уравнение du/dt + λu = 0 и начальное условие u(0) = U0 , где λ и U0 — неизвестные константы. У нас также есть набор наблюдений t_obs и u_obs . Сначала мы импортируем BundleSolver и BundleIVP которые необходимы для получения пакета решений:
из Neurodiffeq.conditions импортировать BundleIVPиз нейродиффеq.solvers импортировать BundleSolver1Dimport matplotlib.pyplot как pltimport numpy как npimport torchfrom Neurodiffeq импортировать diff
Мы определяем область ввода t , а также область значений параметров λ и U0 . Нам также необходимо принять решение о порядке параметров. А именно, какой параметр должен быть первым, а какой вторым. Для целей этой демонстрации мы выбираем λ в качестве первого параметра (индекс 0), а U0 — в качестве второго (индекс 1). Очень важно следить за индексами параметров.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # первый параметр, индекс = 0U0_MIN, U0_MAX = 0,2, 0,6 # второй параметр, индекс = 1
Затем мы определяем conditions и solver как обычно, за исключением того, что мы используем BundleIVP и BundleSolver1D вместо IVP и Solver1D . Интерфейс этих двух очень похож на IVP и Solver1D . Подробную информацию можно найти в справочнике по API.
# параметры уравнения идут после входных данных (обычно временных и пространственных координат) diff_eq = лямбда u, t, lmd: [diff(u, t) + lmd * u]# Аргумент ключевого слова должен иметь имя «u_0» в BundleIVP. Если вы используете что-нибудь еще, например `y0`, `u0` и т. д., это не сработает. индекс 1] решатель = BundleSolver1D (ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ имеет индекс 0; u_0 имеет индекс 1theta_max=[LAMBDA_MAX, U0_MAX], # λ имеет индекс 0; u_0 имеет индекс 1eq_param_index=(0,), # λ — единственный параметр уравнения, имеющий индекс 0n_batches_valid=1, )
Поскольку λ — параметр в уравнении , а U0 — параметр в начальном условии , мы должны включить λ в diff_eq и U0 в условие. Если параметр присутствует и в уравнении, и в условии, его необходимо включить в оба места. Все элементы conditions передаваемые в BundleSovler1D должны быть условиями Bundle* , даже если они не имеют параметров.
Теперь мы можем обучить его и получить решение, как обычно.
Solver.fit(max_epochs=1000)solution =solver.get_solution(best=True)
Решение ожидает три входных данных — t , λ и U0 . Все входы должны иметь одинаковую форму. Например, если вы хотите зафиксировать λ=4 и U0=0.4 и построить график решения u в зависимости от t ∈ [0,1] , вы можете сделать следующее
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0,4 * np.ones_like(t)u = Solution(t, lmd, u0, to_numpy=True) импортировать matplotlib.pyplot как pltplt .plot(т, и)
Получив комплексное solution , вы сможете найти набор параметров (λ, U0) , который наиболее точно соответствует наблюдаемым точкам данных (t_i, u_i) . Это достигается с помощью простого градиентного спуска. В следующем игрушечном примере мы предполагаем, что есть только три точки данных u(0.2) = 0.273 , u(0.5)=0.129 и u(0.8) = 0.0609 . Ниже приведен классический рабочий процесс PyTorch.
# точки наблюдаемых данныхst_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# случайная инициализация λ и U0; отслеживать их градиентlmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)# запускаем градиентный спуск на 10000 эпох для _ в диапазоне (10000):output = Solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs) ))потеря = ((выход - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, loss = {loss.item()}") Простой. При импорте нейродиффека библиотека автоматически определяет, доступен ли CUDA на вашем компьютере. Поскольку библиотека основана на PyTorch, она установит тип тензора по умолчанию torch.cuda.DoubleTensor , если будет найдено совместимое устройство графического процессора.
См. разделы «Пользовательские сети» и «Перенос обучения».
Стандартный способ PyTorch.
Создайте свои сети, как описано в разделе «Пользовательские сети»: nets = [FCNN(), FCN(), ...]
Создайте экземпляр собственного оптимизатора и передайте ему все параметры этих сетей.
параметры = [p для сети в сетях для р в net.parameters()] # список параметров всех сетейMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
Передайте ОБА свои nets и optimizer решателю: solver = Solver1D(..., nets=nets, optimizer=optimizer)
В отличие от традиционных численных методов (МКЭ, ФВМ и т. д.), решение на основе NN требует некоторой гипернастройки. Библиотека предлагает максимальную гибкость для использования любой комбинации гиперпараметров.
Чтобы использовать другую сетевую архитектуру, вы можете передать свой собственный torch.nn.Module .
Чтобы использовать другой оптимизатор, вы можете передать свой собственный оптимизатор в solver = Solver(..., optimizer=my_optim) .
Чтобы использовать другое распределение выборки, вы можете использовать встроенные генераторы или написать свои собственные генераторы с нуля.
Чтобы использовать другой размер выборки, вы можете настроить генераторы или изменить solver = Solver(..., n_batches_train) .
Чтобы динамически изменять гиперпараметры во время обучения, воспользуйтесь нашей функцией обратных вызовов.
Не используйте ReLU для активации, поскольку его производная второго порядка тождественно равна 0.
Измените масштаб вашего PDE/ODE в безразмерной форме, желательно, чтобы все было в диапазоне [0,1] . Работа с доменом типа [0,1000000] подвержена сбоям, потому что а) PyTorch инициализирует веса модулей относительно небольшими и б) большинство функций активации (таких как Sigmoid, Tanh, Swish) наиболее нелинейны вблизи 0.
Если ваш PDE/ODE слишком сложен, попробуйте изучить учебную программу. Начните обучение своих сетей на меньшем домене, а затем постепенно расширяйте, пока не будет охвачен весь домен.
Каждый может внести свой вклад в этот проект.
При создании этого репозитория мы учитываем следующий процесс:
Откройте проблему, чтобы обсудить изменения, которые вы планируете внести.
Ознакомьтесь с Руководством по вкладам.
Внесите изменения в разветвленный репозиторий и обновите README.md, если в интерфейс внесены изменения.
Откройте запрос на вытягивание.