ai simplest network
1.0.0
Это самая простая искусственная нейронная сеть, которую можно объяснить и продемонстрировать.
Искусственные нейронные сети созданы по образцу мозга, поскольку взаимосвязанные искусственные нейроны хранят закономерности и общаются друг с другом. Простейшая форма искусственного нейрона имеет один или несколько входов. 
каждый имеет определенный вес 
и один выход 
.
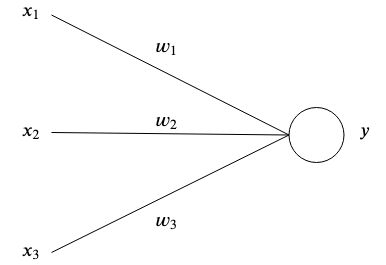
На простейшем уровне выход представляет собой сумму входных данных, умноженную на их веса.
Цель сети — изучить определенный результат. при определенных входных данных 
аппроксимируя сложную функцию со многими параметрами 
что мы не смогли придумать сами.
Допустим, у нас есть сеть с двумя входами. 
и 
и две гири 
и 
.
Идея состоит в том, чтобы настроить веса таким образом, чтобы данные входные данные давали желаемый результат.
Веса обычно инициализируются случайным образом, поскольку мы не можем заранее знать их оптимальное значение, однако для простоты мы инициализируем их оба как 
.
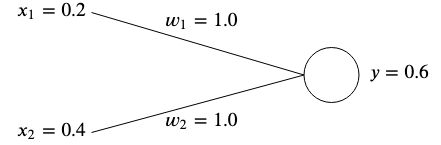
Если мы посчитаем выход этой сети, мы получим
Если вывод не соответствует ожидаемому целевому значению, то возникает ошибка.
Например, если мы хотим получить целевое значение 
тогда у нас будет разница в
Одним из распространенных способов измерения ошибки (также называемой функцией стоимости) является использование среднеквадратической ошибки:
Если у нас было несколько ассоциаций входных и целевых значений, то ошибка становится средней суммой каждой ассоциации.
Мы используем среднеквадратическую ошибку, чтобы измерить, насколько далеки результаты от желаемой цели. Возведение в квадрат устраняет отрицательные знаки и придает больший вес большим различиям между выпуском и целевым показателем.
Чтобы исправить ошибку, нам нужно будет настроить веса таким образом, чтобы выходные данные соответствовали нашей цели. В нашем примере понижение от 
к 
сделал бы свое дело, поскольку
Однако, чтобы настроить веса наших нейронных сетей для множества различных входных данных и целевых значений, нам нужен алгоритм обучения , который сделает это за нас автоматически.
Идея состоит в том, чтобы использовать ошибку, чтобы понять, как следует корректировать каждый вес, чтобы минимизировать ошибку, но сначала нам нужно узнать о градиентах.
По сути, это вектор, указывающий направление наибольшего подъема функции. Градиент обозначается 
и является просто частной производной каждой переменной функции, выраженной в виде вектора.
Для функции с двумя переменными это выглядит следующим образом:
Давайте введем некоторые цифры и рассчитаем градиент на простом примере. Скажем, у нас есть функция 
, тогда градиент будет
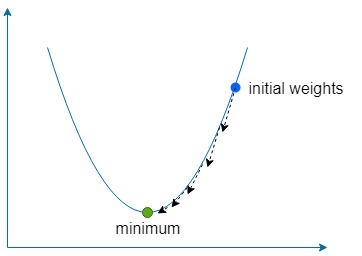
Часть спуска просто означает использование градиента, чтобы найти направление наибольшего подъема нашей функции, а затем несколько раз идти в противоположном направлении на небольшую величину, чтобы найти глобальный (или иногда локальный) минимум функции.
Мы используем константу, называемую скоростью обучения , обозначаемую как 
чтобы определить, насколько малым должен быть шаг в этом направлении.
Если слишком велико, то мы рискуем выйти за пределы минимума функции, но если оно слишком низкое, то сети потребуется больше времени на обучение, и мы рискуем застрять в неглубоком локальном минимуме.
Для наших двух весов и нам нужно найти градиент этих весов относительно функции ошибок 
Для обоих и , мы можем найти градиент, используя правило цепочки
В дальнейшем мы будем обозначать 
как 
термин для простоты.
Получив градиент, мы можем обновить наши веса, вычитая рассчитанный градиент, умноженный на скорость обучения.
И мы повторяем этот процесс до тех пор, пока ошибка не будет минимизирована и не станет достаточно близка к нулю.
Во включенном примере нейронная сеть с двумя входами и одним выходом обучается следующему набору данных с использованием градиентного спуска:
После обучения сеть должна выводить ~0, если даны два с и ~ когда дали и 
.
docker build -t simplest-network .
docker run --rm simplest-network
