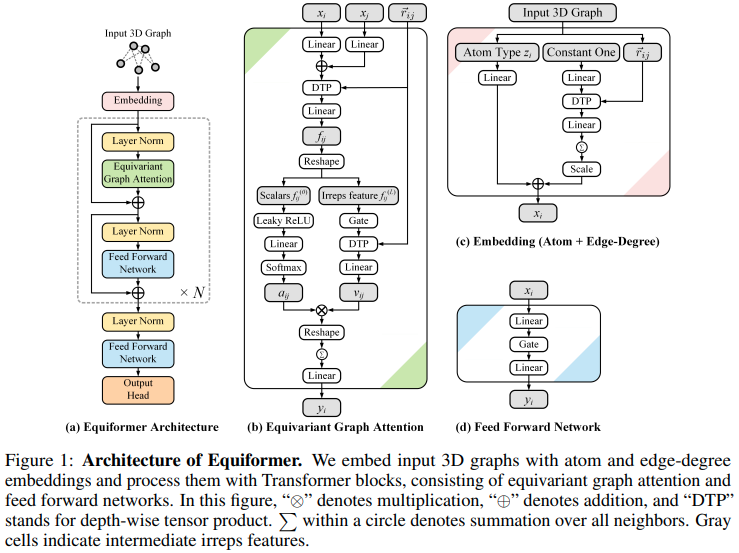
Загрузка equiformer pytorch - Загрузка исходного кода equiformer pytorch

Эквиформер - Пайторч (wip)

Внедрение Equiformer, эквивариантной сети внимания SE3/E3, которая достигает нового SOTA и принята для использования EquiFold (Prescient Design) для сворачивания белков.

Кажется, что его конструкция основана на трансформаторах SE3, в которых внимание скалярного произведения заменено вниманием MLP и нелинейной передачей сообщений от GATv2. Он также выполняет тензорное произведение по глубине для большей эффективности. Если вы думаете, что я ошибаюсь, пожалуйста, напишите мне.

Обновление: появилась новая разработка, которая значительно улучшает масштабирование количества степеней для эквивариантных сетей SE3! В этой статье впервые было отмечено, что при выравнивании представлений по оси z (или оси y по какому-либо другому соглашению) сферические гармоники становятся редкими. Это удаляет измерение m _f из уравнения. Последующий документ от Passaro et al. отметил, что матрица Клебша-Гордана также стала разреженной, что привело к удалению m _i и l _f . Они также пришли к выводу, что проблема уменьшилась с SO(3) до SO(2) после выравнивания повторений по одной оси. Equiformer v2 (Официальный репозиторий) использует это в структуре, похожей на трансформер, для достижения новой SOTA.

Определенно буду вкладывать в это больше работы/исследований. На данный момент я включил приемы из первых двух статей для Equiformer v1, за исключением полного преобразования в SO(2).

Обновление 2: Похоже, что существует новый SOTA без какого-либо взаимодействия между представителями более высокой степени (другими словами, все тензорные произведения / математика Клебша Гордана исчезают). GotenNet, который выглядит как трансформер HEGNN.

Установить

$ pip install equiformer-pytorch

Использование

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),               # dimensions per type, ascending, length must match number of degrees (num_degrees)
    dim_head = ( 4 , 4 , 4 ),          # dimension per attention head
    heads = ( 2 , 2 , 2 ),             # number of attention heads
    num_linear_attn_heads = 0 ,     # number of global linear attention heads, can see all the neighbors
    num_degrees = 3 ,               # number of degrees
    depth = 4 ,                     # depth of equivariant transformer
    attend_self = True ,            # attending to self or not
    reduce_dim_out = True ,         # whether to reduce out to dimension of 1, say for predicting new coordinates for type 1 features
    l2_dist_attention = False      # set to False to try out MLP attention
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask ) # (1, 128)

out . type0 # invariant type 0    - (1, 128)
out . type1 # equivariant type 1  - (1, 128, 3)

В этом репозитории также есть способ отделить использование памяти от глубины с помощью обратимых сетей. Другими словами, при увеличении глубины затраты памяти останутся постоянными при использовании одного блока трансформаторов эквиформера (внимание и прямая связь).

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),
    dim_head = ( 4 , 4 , 4 ),
    heads = ( 2 , 2 , 2 ),
    num_degrees = 3 ,
    depth = 48 ,          # depth of 48 - just to show that it runs - in reality, seems to be quite unstable at higher depths, so architecture stil needs more work
    reversible = True ,   # just set this to True to use https://arxiv.org/abs/1707.04585
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask )

out . type0 . sum (). backward ()

Края

с краями, напр. атомные связи

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

out = model ( atoms , coors , mask , edges = bonds )

out . type0 # (2, 32)
out . type1 # (2, 32, 3)

с матрицей смежности

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    reduce_dim_out = True ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    num_adj_degrees_embed = 2 ,       # this will derive the second degree connections and embed it correctly
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat )

out . type0 # (1, 128)
out . type1 # (1, 128, 3)

Признательность

StabilityAI за щедрую спонсорскую поддержку, а также другим моим спонсорам

Тестирование

Тесты на эквивалентность и т. д.

$ python setup.py test

Пример

Сначала установите sidechainnet

$ pip install sidechainnet

Затем запустите задачу шумоподавления белковой основы.

$ python denoise.py

Тодо

Цитаты

 @article { Liao2022EquiformerEG ,
    title   = { Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs } ,
    author  = { Yi Liao and Tess E. Smidt } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.11990 }
}

 @article { Lee2022.10.07.511322 ,
    author  = { Lee, Jae Hyeon and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and Cho, Kyunghyun and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard } ,
    title   = { EquiFold: Protein Structure Prediction with a Novel Coarse-Grained Structure Representation } ,
    elocation-id = { 2022.10.07.511322 } ,
    year    = { 2022 } ,
    doi     = { 10.1101/2022.10.07.511322 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322 } ,
    eprint  = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Shazeer2019FastTD ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam M. Shazeer } ,
    journal = { ArXiv } ,
    year    = { 2019 } ,
    volume  = { abs/1911.02150 }
}

 @misc { ding2021cogview ,
    title   = { CogView: Mastering Text-to-Image Generation via Transformers } ,
    author  = { Ming Ding and Zhuoyi Yang and Wenyi Hong and Wendi Zheng and Chang Zhou and Da Yin and Junyang Lin and Xu Zou and Zhou Shao and Hongxia Yang and Jie Tang } ,
    year    = { 2021 } ,
    eprint  = { 2105.13290 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @inproceedings { Kim2020TheLC ,
    title   = { The Lipschitz Constant of Self-Attention } ,
    author  = { Hyunjik Kim and George Papamakarios and Andriy Mnih } ,
    booktitle = { International Conference on Machine Learning } ,
    year    = { 2020 }
}

 @article { Zitnick2022SphericalCF ,
    title   = { Spherical Channels for Modeling Atomic Interactions } ,
    author  = { C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.14331 }
}

 @article { Passaro2023ReducingSC ,
  title     = { Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs } ,
  author    = { Saro Passaro and C. Lawrence Zitnick } ,
  journal   = { ArXiv } ,
  year      = { 2023 } ,
  volume    = { abs/2302.03655 }
}

 @inproceedings { Gomez2017TheRR ,
    title   = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author  = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse } ,
    booktitle = { NIPS } ,
    year    = { 2017 }
}

 @article { Bondarenko2023QuantizableTR ,
    title   = { Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing } ,
    author  = { Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort } ,
    journal = { ArXiv } ,
    year    = { 2023 } ,
    volume  = { abs/2306.12929 } ,
    url     = { https://api.semanticscholar.org/CorpusID:259224568 }
}

 @inproceedings { Arora2023ZoologyMA ,
  title   = { Zoology: Measuring and Improving Recall in Efficient Language Models } ,
  author  = { Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e } ,
  year    = { 2023 } ,
  url     = { https://api.semanticscholar.org/CorpusID:266149332 }
}