Реализация алгоритма Minimax AI в игре «Крестики-нолики» (или «Крестики-нолики»). Попробуйте: Крестики-нолики - Минимакс
Для решения игр с использованием ИИ мы введем концепцию дерева игры, за которой следует минимаксный алгоритм. Различные состояния игры представлены узлами в дереве игры, что очень похоже на описанные выше задачи планирования. Идея немного другая. В дереве игры узлы расположены по уровням, которые соответствуют ходам каждого игрока в игре, так что «корневой» узел дерева (обычно изображаемый вверху диаграммы) является начальной позицией в игре. В игре «крестики-нолики» это будет пустая сетка, где еще не сыграны крестики и нолики. Под корнем, на втором уровне, находятся возможные состояния, которые могут возникнуть в результате ходов первого игрока, будь то X или O. Мы называем эти узлы «потомками» корневого узла.
Каждый узел на втором уровне в дальнейшем будет иметь в качестве дочерних узлов состояния, которых можно достичь из него посредством ходов противоположного игрока. Это продолжается, уровень за уровнем, пока не будет достигнуто состояние, в котором игра окончена. В игре «крестики-нолики» это означает, что либо один из игроков выстраивает линию из трёх и выигрывает, либо доска заполнена и игра заканчивается вничью.
Минимакс — это искусственный интеллект, применяемый в играх для двух игроков, таких как крестики-нолики, шашки, шахматы и го. Эти игры известны как игры с нулевой суммой, потому что в математическом представлении: один игрок выигрывает (+1), а другой проигрывает (-1), или оба игрока не выигрывают (0).
Алгоритм рекурсивно ищет лучший ход, который приведет игрока Max к победе или не проигрышу (ничья). Он учитывает текущее состояние игры и доступные ходы в этом состоянии, затем выполняет каждый действительный ход (чередуя min и max ), пока не найдет конечное состояние (выигрыш, ничья или проигрыш).
Алгоритм был изучен по книге «Алгоритмы в двух словах» (Джордж Хайнеман; Гэри Поллис; Стэнли Селков, 2009). Псевдокод (адаптированный):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Теперь мы рассмотрим каждую часть этого псевдокода с реализацией на Python. Реализация Python доступна в этом репозитории. Прежде всего, подумайте:
доска = [[0, 0, 0], [0, 0, 0], [0, 0, 0] ]
МАКС = +1
МИН = -1
MAX может быть X или O, а MIN может быть O или X, что угодно. Доска 3х3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Оба игрока начинают с худшим результатом. Если игрок МАКС, его счет равен -бесконечности. В противном случае, если игрок МИН, его счет равен + бесконечности. Примечание. бесконечность — это псевдоним inf (из модуля math в Python).
Лучший ход на доске — [-1, -1] (строка и столбец) для всех.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreЕсли глубина равна нулю, то на доске нет новых пустых ячеек для игры. Или, если игрок выигрывает, то игра закончилась на MAX или MIN. Таким образом, оценка для этого состояния будет возвращена.
Теперь мы увидим основную часть этого кода, содержащую рекурсию.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yДля каждого допустимого хода (пустые ячейки):
Ход (+1 или -1) на доске отменяется и строка, столбец собирается.
Следующий шаг — сравнить результат с лучшим.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreИгрок MAX получит больший балл. Для игрока MIN будет получен меньший балл. И в итоге лучший ход возвращается. Итоговый алгоритм:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best Ниже лучший ход — посередине, потому что максимальное значение находится во втором узле слева.
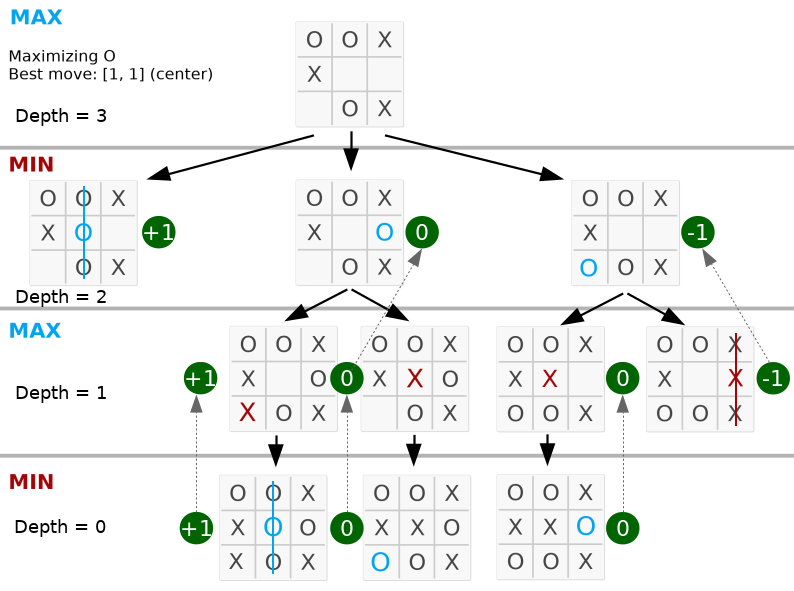
Посмотрите, чтобы глубина была равна допустимым ходам на доске. Полный код доступен в py_version/ .
Упрощенное дерево игры:
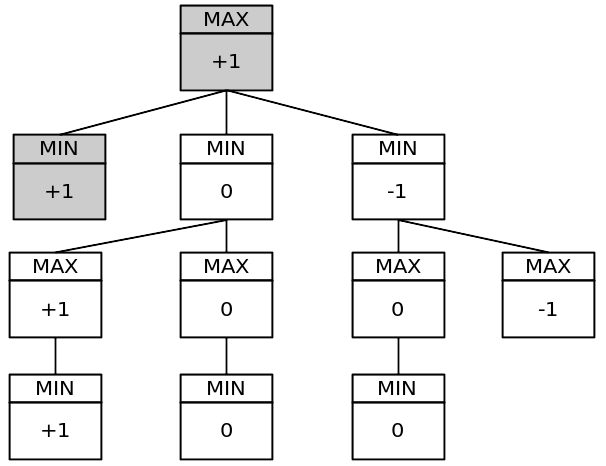
Это дерево имеет 11 узлов. Полное дерево игры имеет 549,946 узлов! Вы можете протестировать это, поместив статическую глобальную переменную в свою программу и увеличивая ее для каждого вызова минимаксной функции за ход.
В более сложной игре, такой как шахматы, сложно выполнить поиск по всему дереву игры. Однако Alpha-beta Pruning — это метод оптимизации минимаксного алгоритма, который позволяет нам игнорировать некоторые ветви в дереве поиска, поскольку он отсекает нерелевантные узлы (поддеревья) при поиске. Для получения дополнительной информации см.: