Тестирование эквивалентности может применяться для оценки того, является ли наблюдаемый эффект от отдельного предиктора в модели множественной регрессии достаточно мал, чтобы рассматриваться статистически и практически незначительно (Alter & Consell, 2021). Для получения дополнительной информации, пожалуйста, обратитесь на страницу OSF и/или свободно доступный препринт на PSYARXIV.
Следующие функции предлагают соответствующие альтернативы на основе эквивалентности для заключения незначительного эффекта между предиктором и результатом в множественной регрессии
Эти функции R предназначены для того, чтобы приспособиться к нескольким исследовательским контекстам без особых усилий, с или без доступа к полному набору данных. Две функции, reg.equiv.fd() и reg.equiv() , предоставляют аналогичный выход, но отличаются от типа входной информации, требуемой пользователем.
В частности, первая функция, reg.equiv.fd() , требует полного набора данных и модели в R (объект lm ), а второе - нет. reg.equiv() предназначен для исследователей, которые не имеют доступа к полному набору данных, но все еще хотят оценить отсутствие связи определенного предиктора с переменной результата в множественной регрессии, например, с использованием информации, обычно представленной в разделе результатов или Таблица сообщена в опубликованной статье.
reg.equiv.fd() : требуется полный набор данныхdatfra= кадра данных (например, mtcars)model= модель, объект LM (например, mod1 , где mod1<- mpg~hp+cyl )delta= наименьший размер эффекта, представляющий интерес (Sesoi), минимально значимый размер эффекта (MME) или верхняя граница интервала эквивалентности (?) (Например, .15)predictor= название предиктора, который будет протестирован (например, "cyl" )test= Тип теста устанавливается автоматически на два односторонних теста (Tost; Schuirmann, 1987), другой вариант-Anderson-Hauck (Ah; Anderson & Hauck, 1983)std= Delta (OR, SESOI) - это набор, который стандартизирован по умолчанию. Укажите std=FALSE чтобы предположить нестандартные единицыalpha= номинальная частота ошибок типа I установлен по умолчанию .05. Чтобы изменить, просто укажите альфа -уровень. Например, alpha=.10 reg.equiv.fd() Пример: 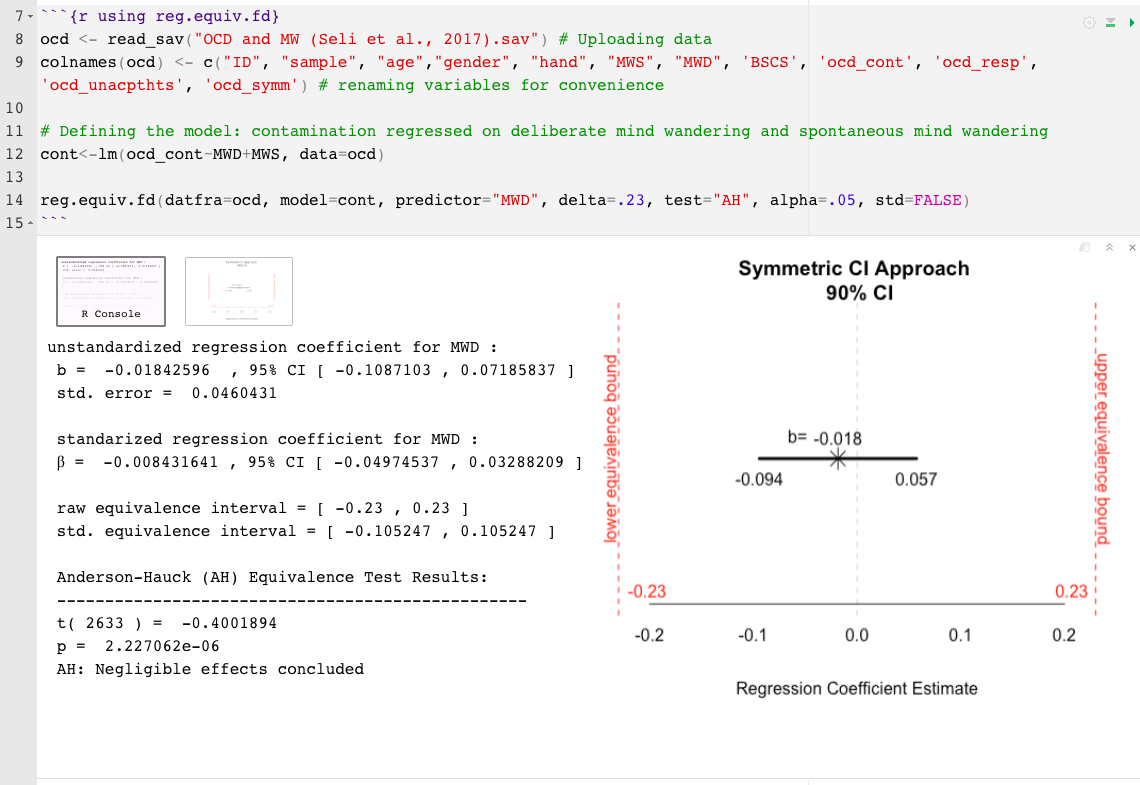
reg.equiv() : полный набор данных не требуетсяb= расчетный величина эффекта, связанный с интересом предиктора, это может быть стандартизировано или нестандартно (например, .02)se= Стандартная ошибка, связанная с величиной эффекта предиктора предиктора (если величина эффекта стандартизирован, убедитесь, что значение se связано с стандартизированным, а не с необработанным эффектом)p= количество общих предикторов в регрессионной модели (исключая перехват)n= размер выборкиdelta= наименьший размер эффекта, представляющий интерес (Sesoi), минимально значимый размер эффекта (MME) или верхняя граница интервала эквивалентности (?) (Например, .15)predictor= название предиктора, который будет протестирован (например, "cyl" )test= Тип теста устанавливается автоматически на два односторонних теста (Tost; Schuirmann, 1987), другой вариант-Anderson-Hauck (Ah; Anderson & Hauck, 1983)std= Delta (OR, SESOI) и указанный размер эффекта устанавливаются как стандартизированные по умолчанию. Укажите std=FALSE чтобы предположить нестандартные единицыalpha= номинальная частота ошибок типа I установлен по умолчанию .05. Чтобы изменить, просто укажите альфа -уровень. Например, alpha=.10 reg.equiv() Пример: 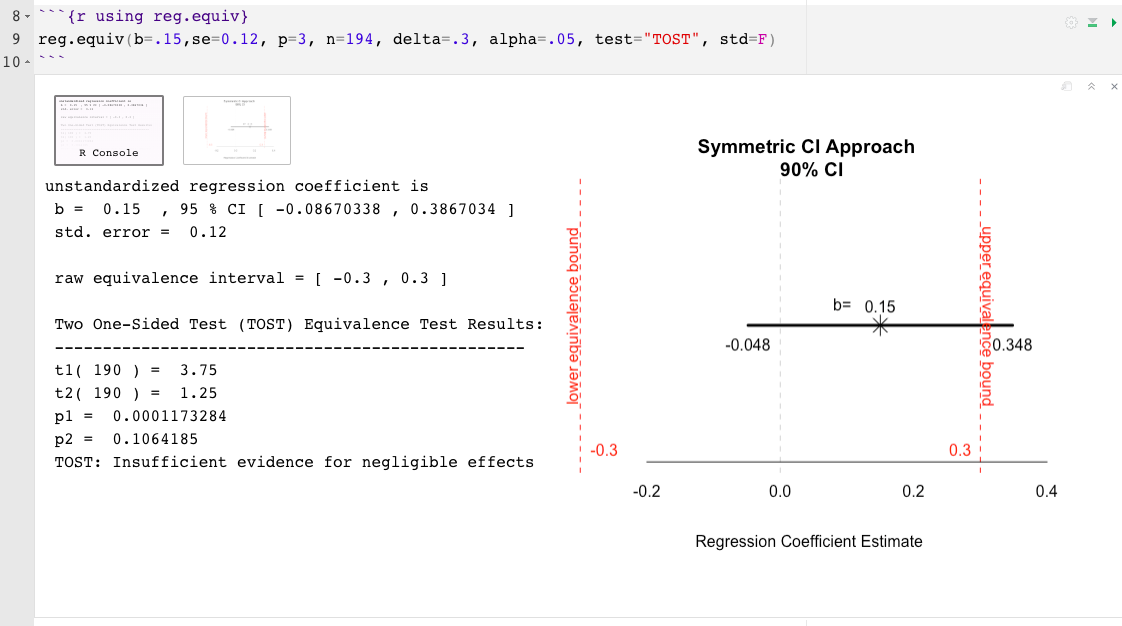
Тестирование эквивалентности-это метод, разработанный в рамках тестирования значимости нулевой гипотезы (NHST). NHST подвергался жесткой критике за его чрезмерную уверенность в дихотомических результатах значений P , практически без учета величины эффекта или его последствий на практике (например, Cumming, 2012; Fidler & Loftus, 2009; Harlow, 1997; Kirk, 2003 Ли, 2016). Исследователи должны помнить об ограничениях NHST и распутать практические и статистические аспекты результатов теста.
Чтобы минимизировать ограничения значений P , более информативно интерпретировать величину и точность наблюдаемого эффекта после завершения «незначительных эффектов» или «недостаточных доказательств для незначительных эффектов». Наблюдаемые эффекты должны быть истолкованы в отношении границ эквивалентности, степени их неопределенности и их практических последствий (или их отсутствия) . По этой причине две функции R, предлагаемые здесь, также включают графическое представление наблюдаемого эффекта и связанную с ним неопределенность в отношении интервала эквивалентности. Полученный график помогает иллюстрировать, насколько близко или далеко и укорениться или сузить наблюдаемый эффект и его погрешность из границ эквивалентности; Вывод о пропорции и положении достоверной полосы в отношении интервала эквивалентности может помочь интерпретировать результаты сверх значений P.