Проблема занятого бобра, проблема информатики, которая длилась сорок лет, наконец-то решена группой любителей! Эта революционная разработка не только шокировала академическое сообщество, но также была признана известным математиком Теренсом Тао и названа самым важным достижением в этой области с 1983 года. С помощью помощника по доказательству Coq они успешно подтвердили, что значение пятого числа занятого бобра BB(5) равно 47 176 870, продемонстрировав большой потенциал программного доказательства в решении сложных математических задач, а также предоставив нам представление о поведении машины Тьюринга. и прекращение проблем.
В загадочной области информатики группа любителей недавно успешно решила задачу сорокалетней давности под названием «задача занятого бобра». Это достижение не только вызвало сенсацию в академическом мире, но и было признано известным математиком Теренсом Тао, который распространил новость в социальных сетях и подчеркнул важность помощников по доказательству в математических исследованиях.
Ученый-компьютерщик Скотт Ааронсон также высоко оценил это открытие, считая его самым важным достижением в исследованиях функций занятого бобра с 1983 года. Это достижение знаменует собой глубокое понимание границ теории вычислений и демонстрирует потенциал доказательств с помощью программного обеспечения в решении сложных математических задач.
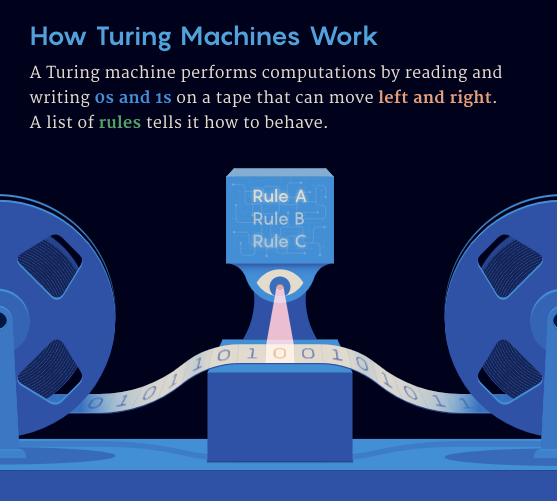
Проблема занятого бобра возникла более 40 лет назад в Дортмунде, Германия, когда ученые-компьютерщики пытались найти конкретную машину Тьюринга, которая могла бы записать наибольшее количество единиц, прежде чем остановиться. Машина Тьюринга — это абстрактная вычислительная модель, предложенная Аланом Тьюрингом в 1936 году, которая выполняет вычисления на бесконечно длинной магнитной ленте, считывая и записывая 0 и 1.

После того, как в 1974 году была определена численность четвертого занятого бобра, вопрос о поиске пятого бобра стал открытым. Теперь онлайн-сообщество, состоящее из более чем 20 участников со всего мира, с помощью программного обеспечения для проверки доказательств под названием Coq успешно подтвердило, что пятое число Busy Beaver BB (5) имеет значение 47 176 870.
Это достижение не только взволновало сообщество, но и вызвало изумление учёного-компьютерщика Дэмиена Вудса, который сравнил прогресс со скоростью Усейна Болта. Хотя решение этой проблемы может быть не применимо напрямую к другим областям информатики, для участников эта борьба с математической невозможностью сама по себе является величайшей наградой.
Суть проблемы занятого бобра заключается в понимании поведения машин Тьюринга, в частности их эффективности при решении задач остановки. Поведение машины Тьюринга определяется набором правил, которые можно представить в виде таблицы. Каждое правило определяет действие, которое должно быть выполнено, когда головка чтения/записи обнаруживает 0 или 1 в определенном состоянии.
Хотя машины Тьюринга могут застревать в бесконечных циклах, определение того, перестанут ли они когда-либо работать, является известной нерешенной проблемой. Математика Тибора Радо не удовлетворил этот вывод, и поэтому он изобрел «игру занятого бобра», чтобы исследовать природу проблемы остановки, группируя машины Тьюринга в соответствии с количеством имеющихся у них правил.
Ранние исследователи, такие как Аллен Брэйди, исследовали эту проблему, написав программы для моделирования поведения машин Тьюринга. Его работа и открытия других исследователей заложили основу для последующих исследователей.
До 2022 года аспирант Тристан Стерин запустил Busy Beaver Challenge, совместный онлайн-проект, направленный на завершение BB(5). Благодаря инновационным методам и помощи помощника по проверке Coq команде наконец удалось найти пятого занятого бобра.
Это достижение — не только вызов невозможности математики, но и исследование границ информатики. После подтверждения BB(5) исследователи готовят научную статью, которая будет удобочитаемой версией, дополняющей доказательство Coq. В то же время они также думают о том, станет ли исследование BB(6) следующей целью.
Ссылка: https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
Решение проблемы занятого бобра — это не только крупный прорыв в области математики, но также открывает новые направления и идеи для будущих исследований в области теории вычислений. Это достижение побуждает больше людей участвовать в исследованиях в области математики и информатики и вместе исследовать неизвестные области.