This article brings you relevant knowledge about JavaScript, which mainly introduces the relevant content about number types. There are two types of numbers in JavaScript: Number and BigInt types. Let’s take a look at them together. I hope it will be useful to you. help.
[Related recommendations: javascript video tutorial, web front-end]
There are two types of numbers in JavaScript :
The Number type, which is a number type in the conventional sense, is stored in the 64 bit IEEE-754 format and is a "double-precision floating point number". So far, all the numbers we have come into contact with are of Number type;
The BigInt type represents integers of any length. Normally we do not use them unless they represent numbers other than 2 53 to -2 53. We will introduce these professional data types in detail in later chapters;
The way to write numbers is very simple, but JavaScrpt has a lot of convenient and fast syntactic sugar for us to use. Learning these syntactic sugars will not only improve our code reading ability, but also improve the high-level sense of our code.
Decimal numbers are the simplest, and we will use them more or less in almost every article. For example, we create a variable and store 100 billion:
let tenbillion = 10000000000;
Although the operation is very simple, there is a problem: it is difficult to count how many 0 follow 1 If we are writing a transfer code, a wrong 0 may lead to bankruptcy.
At this time, we can use _ as the delimiter, as follows:
let tenbillion = 10_000_000_000;
The above code can clearly count the number of 0 , which is obviously the optimal solution!
_ underscore here is a syntactic sugar of JavaScript , which will be ignored by the engine during execution. The above two writing methods have the same effect, but the reading experience is very different.
Qingqi brain circuit
Some children's shoes have to ask, I have always been in groups of 4 0 since I was a child, why do I have to group 3 0 ? Therefore, we can write it in the following way without any problem:
let tenbillion = 100_0000_0000;
Or it could be written like this:
let tenbillion = 1_0000_0000_00;
What I want to express here is that no matter which division method you use, it will not affect the size of the number itself. Come up with the most powerful method!
Although using _ can elegantly divide many 0 , in real life, we generally don't write it this way. For example, we often write 10000000000 as "10 billion", so that many 0 can be omitted, thereby reducing the possibility of making mistakes.
JavaScript also provides a way to omit 0 We can use the letter e followed by a number to represent the number of 0 For example:
let tenbillion = 1e10;//10 billion, 1 followed by 10 0sconsole.log(3.14e9);//3140000000, followed by 7 0s, please look down if you have any questions.
The understanding of the above code is very simple. e10 can be understood as 1_0000_0000_00 0 which is 1 followed by 10 , so we can think:
1e10 === 1 * 1_0000_0000_00;//e10 means 1 followed by 10 03.14e9 === 3.14 * 1_000_000_000;//e9 means 1 followed by 9 0s
We can also use this method to represent very small numbers, such as 1 nanometer:
let nm = 0.000000001; //Unit (meter)
Since there are too many 0 , we can also use _ :
let nm = 0.000_000_001;
Of course, you can also use e to omit all 0 , as follows:
let nm = 1e-9;//9 0s to the left of 1, including the one before the decimal point
In other words, e-9 means 1 -9 , which is 1/1000_000_000 , so the following equation is true:
1e-9 === 1 / 1_000_000_000;3.14e-8 === 3.14 / 1_000_000_00;
Hexadecimal is a format commonly used in programming, such as color, encoding, etc. We can add 0x before ordinary numbers to represent hexadecimal numbers:
let hex = 0xff;//255, not case sensitive, 0xFF is the same
Binary numbers start with 0b :
let bin = 0b1011;//11
Octal numbers start with 0o :
let oct = 0o777;//511
This simple writing method only supports these three special types. As for other base numbers, you can use special functions to generate them ( parseInt ).
The toString method can convert the number into a string form corresponding to base .
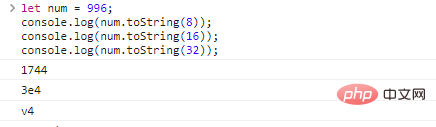
Give a chestnut:
let num = 996; console.log(num.toString(8));//Convert to octal string console.log(num.toString(16));//Convert to hexadecimal string console.log(num.toString( 32));//Convert to 32 hexadecimal string
The code execution results are as follows:
The range of base can be from 2 to 36 If not filled in, the default is 10 .
Note that if you use numbers to directly call the toString method, in some cases you need to apply two . , for example:
console.log(123.toString(8));//Error, syntax error console.log(123..toString(8));//Correct, 173
There are two . after the number. This is because in JavaScript the first . after the number is considered the decimal point, and the second dot is the . that calls the function .
If it is a decimal, this problem does not exist. For example:
console.log(3.14.toString(8));
Or, we can use parentheses to avoid using two dots, for example:
console.log((123).toString(8));//'173
Rounding is one of the most common operations on numbers and usually includes:
Round down, Math.floor(num)
console.log(Math.floor(3.14));//3 console.log(Math.floor(9.99));//9 console.log(Math.floor(-3.14));//-4 console.log(Math.floor(-9.99));//-10
Do not follow the rounding principle and directly take the nearest integer less than or equal to the current value.
Round up, Math.ceil(num)
console.log(Math.ceil(3.14));//4 console.log(Math.ceil(9.99));//10 console.log(Math.ceil(-3.14));//-3 console.log(Math.ceil(-9.99));//-9
Do not follow the rounding principle and directly take the nearest integer greater than or equal to the current number.
Round to the nearest integer, Math.round(num)
console.log(Math.round(3.14));//3 console.log(Math.round(9.99));//10 console.log(Math.round(-3.14));//-3 console.log(Math.round(-9.99));//-10
Following the rounding principle, the nearest integer to the current number is taken.
Remove decimals, Math.trunc(num)
console.log(Math.trunc(3.14));//3 console.log(Math.trunc(9.99));//9 console.log(Math.trunc(-3.14));//-3 console.log(Math.trunc(-9.99));//-9
Directly remove the numbers after the decimal point and round to integer digits. IE browser does not support this method
Compare the above four methods:
| Math.floor | Math.ceil | Math.round | Math.trunc | |
|---|---|---|---|---|
| 3.14 | 3 | 4 | 3 | 3 |
| 9.99 | 9 | 10 | 10 | 9 |
| -3.14 | -4 | -3 | -3 | -3 |
| -9.99 | -10 | -9 | -10 | -9 |
The above method simply rounds the decimal into an integer. In some cases, we need decimals with a specific precision. For example, what should we do if we take the last 4 digits of pi?
There are two methods:
math multiplication and division counting
let pi = 3.1415926;console.log(Math.round(pi * 10000) / 10000);//3.1416
The above code first multiplies pi by 10000 , then rounds it, and then divides it by 10000 , thus obtaining a result that meets the accuracy requirements. However, this seems silly, and JavaScript provides us with an easier way.
toFixed(n)
let pi = 3.1415926;console.log(pi.toFixed(4));//3.1416
The above code seems to have no problem with the output. In fact, toFixed returns a string. If we need a numeric type, we need to convert it. We can use the unary operator + pi.toFixed(4) .
In addition, if the decimal mantissa is not long enough, toFixed will add '0' at the end:
let num = 3.1;console.log(num.toFixed(9));
The code execution results are as follows:
This also proves that the return value of toFixed is a string, otherwise 0 will be omitted.
Floating point representations are always biased in many cases
Inside the computer, floating point numbers are represented according to IEEE-754 standard, where single precision floating point numbers are 32 bits and double precision floating point numbers are 64 bits. In a double precision floating point number, 1 bit is used to represent the sign, 52 bits are used to store the significant digits, and 11 bits are used to store the position of the decimal point.
Although 64 bits can already represent very large numbers, there is still the possibility of crossing the boundary, for example:
let bigNum = 1e999;console.log(bigNum);//Infinity
The number that exceeds the maximum value will become Infinity (infinity), thus losing the size of the original number, which is a kind of deviation.
There is another kind of deviation that we need to learn:
console.log(0.1+0.2 === 0.3);//falseconsole.log(0.1 + 0.2);
The code execution results are as follows:
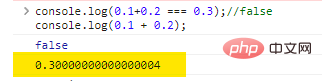
That's right, the result of 0.1 + 0.2 is not 0.3 , but a bunch of 0 followed by a 4 .
This kind of deviation is very fatal, especially in shopping malls and bank work scenarios. Even a very small deviation will lead to the loss of endless wealth in high turnover scenarios.
I once heard a story about a bank employee who stole millions of dollars by deducting workers’ wages. Each employee’s salary was only 20 cents!
I think if this happened to me, I would definitely not be able to find it, so it is so important to be accurate at all times.
I don’t know if this story is true or not~~
Let’s take our common decimal system as an example. We all know that there are two weird things in decimals, one is called infinite repeating decimals, and the other is called infinite non-repeating decimals. For example, 1/3 is an infinite repeating decimal 0.3333333(3) , and pi It is an infinite non-repeating decimal. Infinite means that the size of the number cannot be clearly described numerically, and what we can write is inaccurate.
There are also some infinitely looping numbers in binary. The difference is that in decimal, a number like 0.1 which looks very simple, is an infinitely looping decimal in binary.
For example:
let x = 0.1;console.log(x.toFixed(20));
The code execution results are as follows:
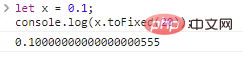
Don’t you think it’s incredible? We simply created a variable and assigned it a value of 0.1 , and then took 20 decimal places, but we got an incredible result.
If we change the angle, it may be easier to understand this phenomenon. In the decimal system, any integer divided by 10 or 10 integer powers is a normal and accurate number, such as 1/10 or 996/1000 . However, if you divide by 3 , you will get a looping result, such as 1/3 .
This description is also valid if converted to binary.
In binary, any integer divided by 2 or an integer power of 2 is a normal exact number. However, if you divide it by 10 , you will get an infinite loop of binary numbers.
Therefore, we can conclude that binary numbers cannot accurately represent 0.1 and 0.2 just like decimal cannot describe 1/3 .
Notice:
This kind of data deviation is not a defect of JavaScript, it is the same result for PHP, Java, C, Perl, and Ruby.
Rounding
When displaying an infinitely recurring decimal, we can directly use the toFixed method to round the decimal. This method directly returns a string, which is very convenient for displaying prices.
0.3.toFixed(2);//0.30
Use small units
Another way is that we can use smaller units to calculate prices and distances, such as using cents instead of yuan to calculate the total price. In fact, many trading websites do this. However, this method only reduces the number of occurrences of decimals, and there is no way to completely avoid the occurrence of decimals.
There are two special values in JavaScript numbers: Infinity and NaN .
How to judge whether a number is a normal number?
We can use two methods:
isFinite(val)
This function will convert the parameter val to a numeric type, then determine whether the number is finite, and return true when the number is not NaN , Infinity , or -Infinity .
console.log(isFinite(NaN));//falseconsole.log(isFinite(Infinity));//falseconsole.log(isFinite(3));//trueconsole.log(isFinite('12'));// true The code execution results are as follows: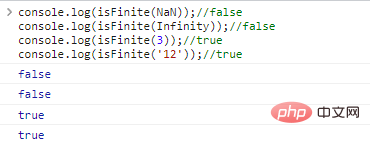
Since a string that cannot be converted to a number will be converted to NaN , we can use the isFinite method to determine whether the string is a numeric string:
console.log(isFinite('xxxx'));//falseconsole.log(isFinite('Infinite'));//falseconsole.log(isFinite(' '));//true, empty string is converted to 0The code execution results are as follows:
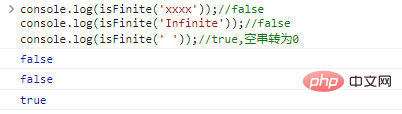
isNaN(val)
Returns true when val is NaN or other value that cannot be converted to a number.
console.log(isNaN(NaN));//trueconsole.log(isNaN('Infinite'));//true Code execution results: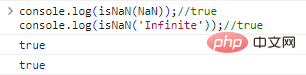
Why use the isNaN function instead of reading it directly?
For example:
console.log(NaN === NaN);//false
The code execution results are as follows:
This is because NaN is not equal to any number, including itself.
Object.is(a,b) can determine whether parameters a and b are equal. If they are equal, it returns true , otherwise it returns false . Its results have only three situations:
Can be compared to NaN
console.log(Object.is(NaN,NaN));//true
Code execution results:

0 and -0
console.log(Object.is(0,-0));//false
Code execution results:

Within the computer, positive and negative are represented by 0 and 1 Due to different signs, 0 and -0 are actually different, and they are expressed in different ways.
other
Other comparison situations are exactly the same as a === b .
parseInt and parseFloat can convert strings into numbers. Unlike + and Number , their restrictions are looser. For example, using + and Number for a string like "100¥" will inevitably return NaN , but parseInt and parseFloat can handle it easily.
For example:
console.log(+"100¥");console.log(parseInt("100¥"));console.log(parseFloat("12.5¥"));Code execution results:
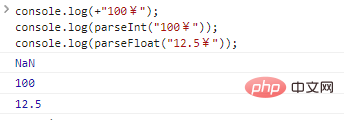
parseInt and parseFloat read numbers from a string until they cannot be read anymore. Both are particularly suitable for processing strings starting with numbers like "99px" and "11.4em" , but NaN is returned for strings starting with other characters.
console.log(parseInt('ff2000'));//NaN However, we found ff2000 is actually a hexadecimal digital string. parseInt can also handle this situation, but needs to add a hexadecimal parameter.
For example:
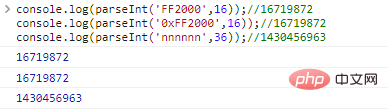
console.log(parseInt('FF2000',16));
//16719872
console.log(parseInt('0xFF2000',16));
//16719872
console.log(parseInt('nnnnnn',36));
//1430456963Code execution results:
The built-in Math object contains many constants and methods that we often use. Here are just a few examples of commonly used ones:
Math.PI
Pi Π is an infinite non-cyclic constant, we can use Math.PI instead:
console.log(Math.PI);

Math.random()
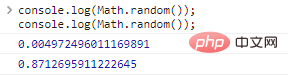
Generate a random number in the interval [0,1) :
console.log(Math.random());console.log(Math.random());
If we need a random number within a specific range, we can multiply it by a specific value and then round it.
Math.pow(a,b)
Calculate a b , for example:
console.log(Math.pow(2,3));//8
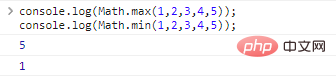
Math.max()/Math.min()
Choose a maximum/minimum value from any number of arguments:
console.log(Math.max(1,2,3,4,5));//5console.log(Math.min(1,2,3,4,5));//1