Large -scale language models (LLM) show amazing abilities in many fields. However, a latest study reveals their "wonderful" weaknesses in arithmetic reasoning: These "genius" AIs have frequently made mistakes in simple mathematical operations!研究人员深入分析了Llama3、Pythia和GPT-J等多个LLM,发现它们并非依靠强大的算法或记忆力进行计算,而是采用一种“启发式大杂烩”的策略,如同一个靠“小聪明”和“ The law of empirical "Mongolian answers.
Recently, the AI large language model (LLM) performed well in various tasks. Writing poetry, writing code, and chatting is nothing! But, do you dare to believe it? These "genius" AI are actually " Mathematics rookie "! They often turn over when dealing with simple arithmetic questions, which is surprising.
A latest study reveals the "wonderful" secret behind LLM arithmetic reasoning capabilities: they neither rely on strong algorithms nor relying on memory, but use a strategy called "inspiration of hodgepodge"! This is like a student. He did not study mathematical formulas and theorems carefully, but rely on some "little cleverness" and "law rules" to answer.
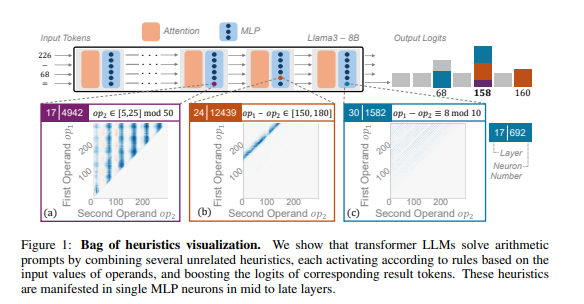
Researchers use arithmetic reasoning as typical tasks to conduct in-depth analysis of multiple LLMs such as LLAMA3, Pythia and GPT-J. They found that the LLM model is responsible for arithmetic calculation (called "circuit") consisting of many single neurons. Each neuron is like a "micro calculator", which is only responsible for identifying specific digital modes and output corresponding correspondence corresponding to the corresponding digital mode and output the corresponding correspondence Answer. For example, a neurons may be responsible for identifying "numbers with 8 digits", and another neuron is responsible for identifying "subtraction operations between 150 and 180."
These "miniature calculators" are like a pile of messy tools. LLM does not use them according to specific algorithms, but to use these "tools" to calculate the answers based on the input digital mode. This is like a chef, there is no fixed recipe, but in the existing ingredients at hand, and finally make a "dark cuisine".
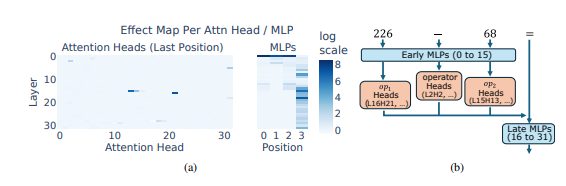
What is even more surprising is that this "inspirational hodgepodge" strategy actually appeared early in LLM training, and gradually improved with the training. This means that LLM relies on this "pieces of pieces of pieces" from the beginning, rather than developing this strategy in the later period.
So, what are the problems of this "wonderful" arithmetic reasoning method? Researchers have found that the generalization ability of the "inspiration of hodgepodge" strategy is limited and it is prone to errors. This is because the number of "small cleverness" held by LLM is limited, and these "little cleverness" may also have defects in themselves, causing them to be unable to give the correct answer when they encounter a new digital model. Just like a chef who only made "tomato scrambled eggs", he suddenly made him make a "fish -flavored shredded shredder".
This study revealed the limitations of LLM arithmetic reasoning capabilities, and also pointed out the direction for the future improvement of LLM's mathematical capabilities. Researchers believe that relying on existing training methods and model architectures may not be enough to improve LLM's arithmetic reasoning capabilities. It needs to explore new methods to help LLM learn more powerful and more generalized algorithms so that they can truly become "mathematics masters" Essence
Thesis address: https://arxiv.org/pdf/2410.21272
This research not only explains the lack of LLM in mathematics calculation, but also more importantly provides valuable reference directions for the future improvement of LLM. In the future research, we need to pay attention to how to improve the generalization and algorithm learning ability of LLM to solve its defects in arithmetic reasoning and make it truly powerful mathematical capabilities.