長達四十年的電腦科學難題——忙碌海狸問題,終於被一群業餘愛好者破解!這項突破性進展不僅震驚了學術界,也得到了著名數學家陶哲軒的認可,並被譽為自1983年以來該領域最重要的進展。他們利用Coq證明助手,成功驗證了第五個忙碌海狸數BB(5)的值為47,176,870,展現了軟體輔助證明在解決複雜數學問題中的巨大潛力,也為我們理解圖靈機行為和停機問題提供了新的視角。
在電腦科學的一個神秘領域,一個長達四十年的難題——忙碌海狸問題,最近被一群業餘愛好者成功破解。這項成就不僅在學術界引起了轟動,也得到了著名數學家陶哲軒的認可,他在社群媒體上轉發了這一消息,並強調了證明助手在數學研究中的重要性。
電腦科學家Scott Aaronson也對這項發現給予了高度評價,認為這是自1983年以來,忙碌海狸函數研究中最重要的進展。這項成就標誌著對計算理論邊界的深入理解,也展示了軟體輔助證明在解決複雜數學問題的潛力。
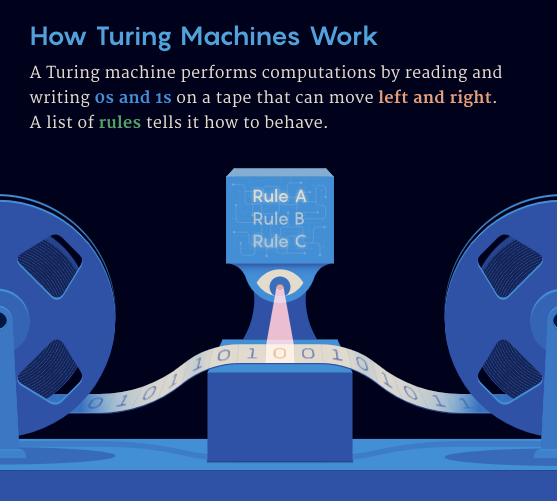
忙碌海狸問題起源於40多年前的德國多特蒙德,當時電腦科學家試圖尋找能夠在停止前寫下最多1的特定圖靈機。圖靈機是一種抽象的計算模型,由艾倫·圖靈在1936年提出,透過讀取和寫入0和1在無限長的磁帶上計算。

1974年,第四個忙碌海狸數被確定後,尋找第五個海狸成了一個懸而未決的問題。現在,一個由20多名來自世界各地的貢獻者組成的線上社區,使用名為Coq的證明助手軟體,成功驗證了第五個忙碌海狸數BB(5)的值為47,176,870。
這項成就不僅令社區沸騰,也引起了電腦科學家Damien Woods的驚嘆,他將這一進展比作博爾特的速度。儘管這個問題的解決可能不會直接應用於電腦科學的其他領域,但對於參與者來說,這場與數學不可能性的鬥爭本身就是最大的獎勵。
忙碌海狸問題的核心在於理解圖靈機的行為,特別是它們在停機問題上的表現。圖靈機的行為由一組規則定義,這些規則可以想像成一張表。每條規則指定了在特定狀態下,讀寫頭遇到0或1時應該執行的操作。
儘管圖靈機可能會陷入無限循環,但確定它們是否會停止運作是一個著名的未解問題。數學家Tibor Radó不滿意這個結論,並由此發明了“忙碌的海狸遊戲”,透過將圖靈機根據它們擁有的規則數量進行分組,來探索停機問題的本質。
早期的研究者,如Allen Brady,透過編寫程式模擬圖靈機的行為,對此問題進行了探索。他的工作和其他研究者的發現,為後來的探索者奠定了基礎。
直到2022年,研究生Tristan Stérin發起了“忙碌海狸挑戰”,這是一個線上合作項目,旨在最終確定BB(5)。透過創新的方法和Coq證明助手的幫助,這個團隊最終成功找到了第五個忙碌海狸。
這項成就不僅是數學不可能性的挑戰,也是對電腦科學極限的探索。隨著BB(5)的確認,研究者們正在起草一份學術論文,這將是一個補充Coq證明的人類可讀版本。同時,他們也在思考,BB(6)的探索是否將成為下一個目標。
參考資料:https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
忙碌海狸問題的解決,不僅是數學領域的重大突破,也為未來計算理論研究提供了新的方向與想法。 這項成就鼓舞著更多人參與數學和電腦科學的研究中,共同探索未知的領域。