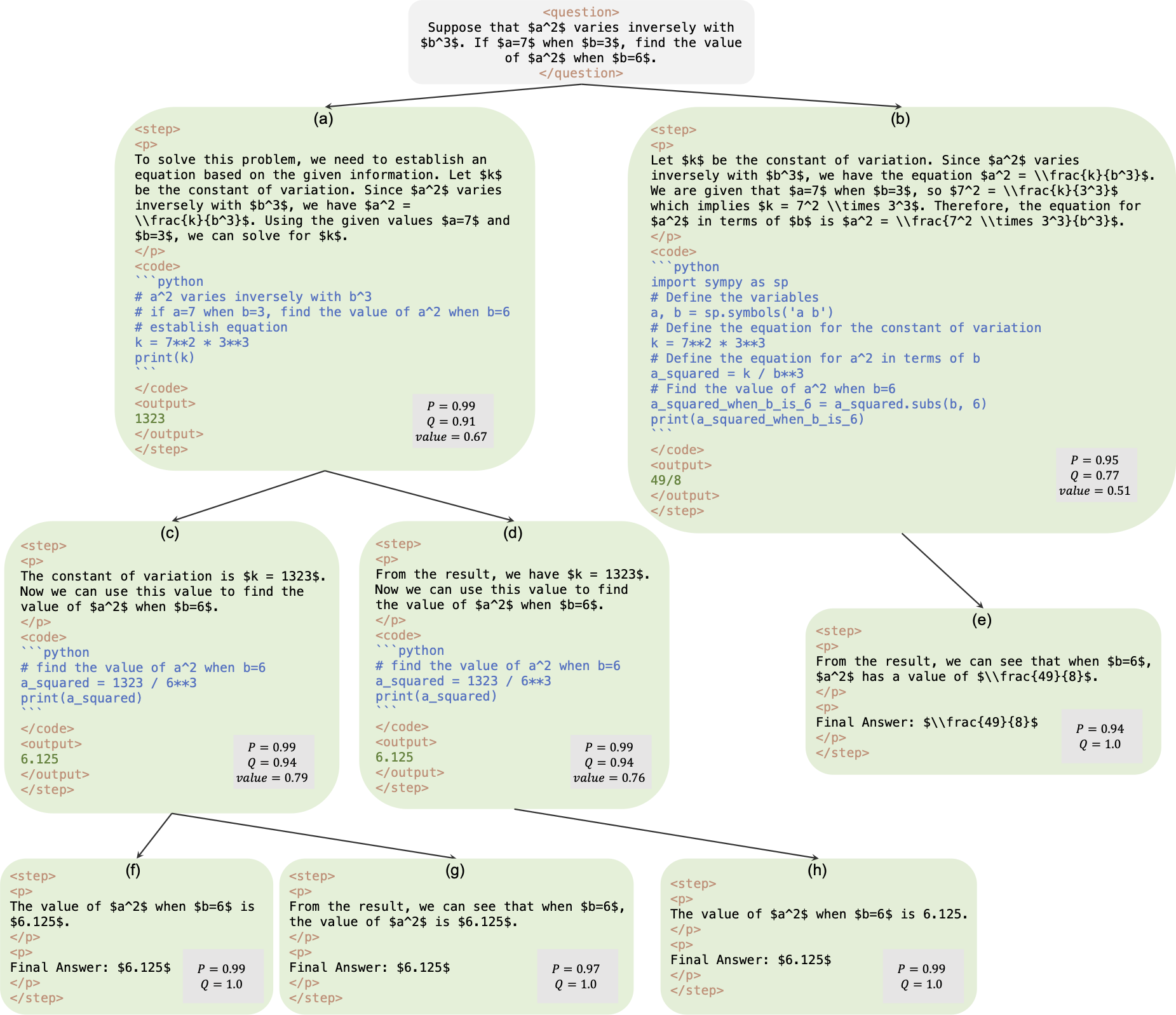
هذا هو المستودع الرسمي للورقة AlphaMath Almost Zero: الإشراف على العمليات بدون عملية. يتم استخراج الكود من قاعدة التعليمات البرمجية الداخلية لشركتنا. ونتيجة لذلك، قد تكون هناك اختلافات طفيفة عند إعادة إنتاج الأرقام المذكورة في ورقتنا، ولكنها يجب أن تكون قريبة جدًا. يتضمن نهجنا تدريب نماذج السياسة والقيمة باستخدام المنطق الرياضي المشتق من إطار بحث شجرة مونت كارلو (MCTS)، مما يلغي الحاجة إلى GPT-4 أو التعليقات التوضيحية البشرية. هذا مثال توضيحي لمثيل التدريب الذي تم إنشاؤه بواسطة MCTS في الجولة الثالثة.
نقطة التفتيش : AlphaMath-7B الجولة 3؟ / AlphaMath-7B الجولة 3؟
مجموعة البيانات : AlphaMath-Round3-Trainset؟ يتم إنشاء عملية حل بيانات التدريب تلقائيًا بناءً على MCTS ونقطة التفتيش في الجولة الثانية. ويتم تضمين الأمثلة الإيجابية والسلبية لتدريب نماذج السياسة والقيمة.
كود التدريب : نظرًا للسياسة، يمكننا فقط إصدار تفاصيل التنفيذ لبعض الوظائف الرئيسية، والتي يجب تعديلها بشكل أساسي في كود التدريب الخاص بك.
| طريقة الاستدلال | دقة | متوسط الوقت (ق) لكل س | متوسط خطوات | # يوم مريخي |
|---|---|---|---|---|
| طماع | 53.62 | 1.6 | 3.1 | 1 |
| ماج@5 | 61.84 | 2.9 | 2.9 | 5 |
| شعاع مستوى الخطوة (1,5) | 62.32 | 3.1 | 3.0 | أعلى 1 |
| 5 أشواط + Maj@5 | 67.04 | ×5 | ×1 | 5 أعلى 1 |
| شعاع مستوى الخطوة (2,5) | 64.66 | 2.4 | 2.4 | أعلى 1 |
| شعاع مستوى الخطوة (3,5) | 65.74 | 2.3 | 2.2 | أعلى 1 |
| شعاع مستوى الخطوة (5,5) | 65.98 | 4.7 | 2.3 | أعلى 1 |
| شوط واحد + ماج@5 | 66.54 | ×1 | ×1 | أعلى 5 |
| 5 أشواط + Maj@5 | 69.94 | ×5 | ×1 | 5 أعلى 1 |
| ام سي تي اس (العدد = 40) | 64.02 | 10.1 | 3.8 | أعلى 1 |
+ Maj@5 يتطلب التشغيل 5 مرات، مما يشجع على التنوع.+ Maj@5 المرشحين الخمسة بشكل مباشر، وهو ما يفتقر إلى التنوع.| درجة حرارة | 0.6 | 1.0 |
|---|---|---|
| شعاع مستوى الخطوة (1,5) | 62.32 | 62.76 |
| شعاع مستوى الخطوة (2,5) | 64.66 | 65.60 |
| شعاع مستوى الخطوة (3,5) | 65.74 | 66.28 |
| شعاع مستوى الخطوة (5,5) | 65.98 | 66.38 |
بالنسبة للبحث عن الشعاع على مستوى الخطوة، قد يؤدي ضبط temperature=1.0 إلى تحقيق نتائج أفضل قليلاً.
requirements.txt pip install -r requirements.txt
أو ببساطة اتبع cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py لإضافة رأس القيمة إلى LLM. يمكنك تشغيل أي من الأمرين cmds التاليين. قد يكون هناك اختلاف بسيط في الدقة بين الاثنين. وفي آلتنا حصل الأول على 53.4% والثاني على 53.62%.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
أو
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
في أجهزتنا، في مجموعة اختبارات MATH، يمكن لأمر cmd التالي مع التكوين B1=1, B2=5 أن يحقق ~62%، ويمكن أن يصل الأمر الذي يحتوي على التكوين B1=3, B2=5 إلى ~65%.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
احسب الدقة
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
يجب توفير ground_truth (الإجابة النهائية، وليس عملية الحل) في ملف qaf json أو jsonl (مثال للتنسيق يمكن الرجوع إلى ../MARIO_EVAL/data/math_testset_annotation.json ).
الجولة 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
جولة> 1، بعد SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
سيتم استخدام question فقط لتوليد الحلول، ولكن سيتم استخدام ground_truth لحساب الدقة.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
يختلف عن بحث الشعاع على مستوى الخطوة، فأنت تحتاج أولاً إلى إنشاء شجرة كاملة، ثم يجب عليك تشغيل MCTS دون الاتصال بالإنترنت ثم حساب الدقة.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
ملاحظة: يمكن أيضًا تشغيل البرنامج النصي للتقييم هذا باستخدام الشجرة المحفوظة عن طريق البحث عن شعاع على مستوى الخطوة، ويجب أن تظل الدقة كما هي.
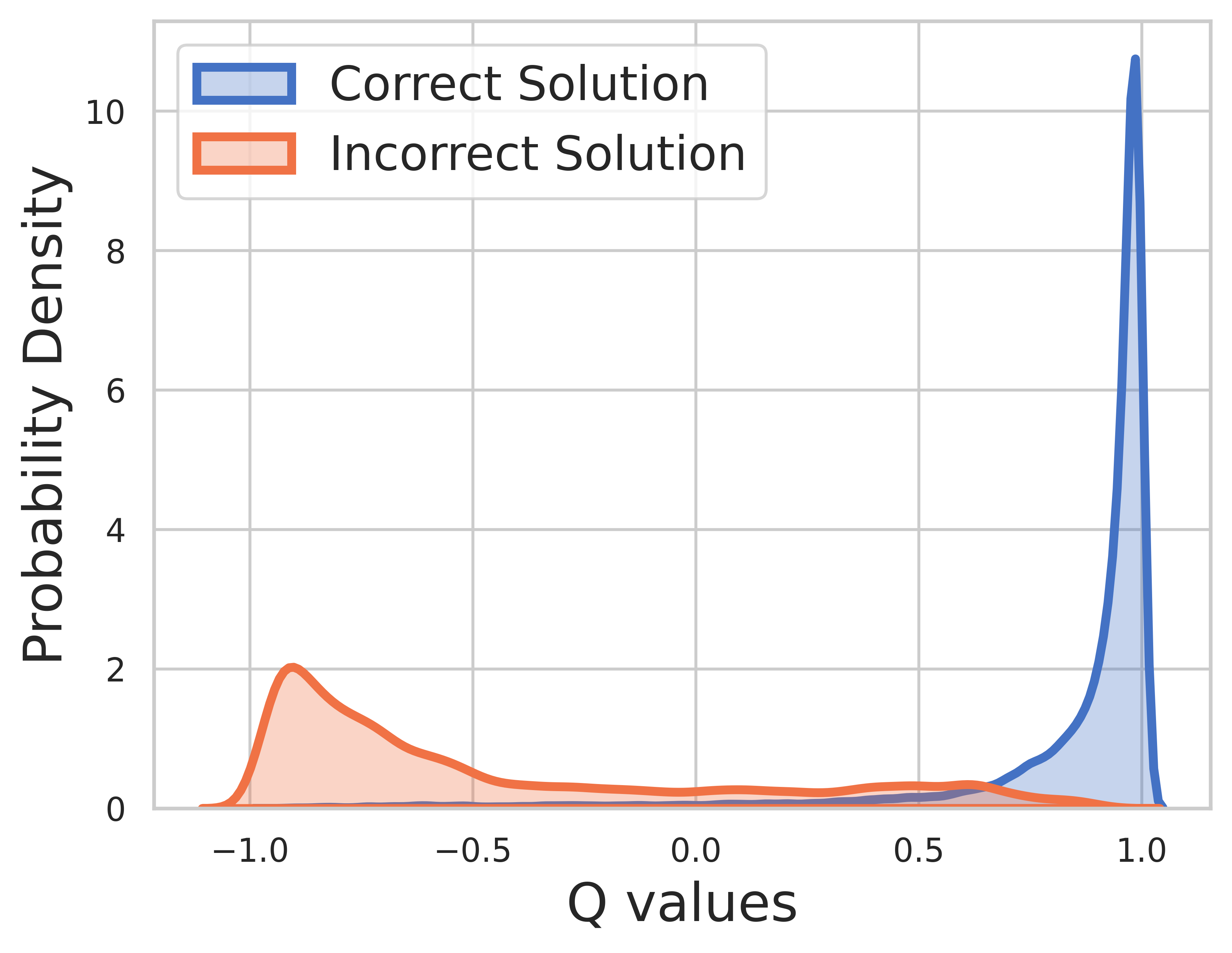
نظرًا لأن الحقيقة الأساسية معروفة ببيانات التدريب، فإن قيمة الخطوة النهائية هي المكافأة ويمكن أن تتقارب قيمة Q بشكل جيد للغاية.
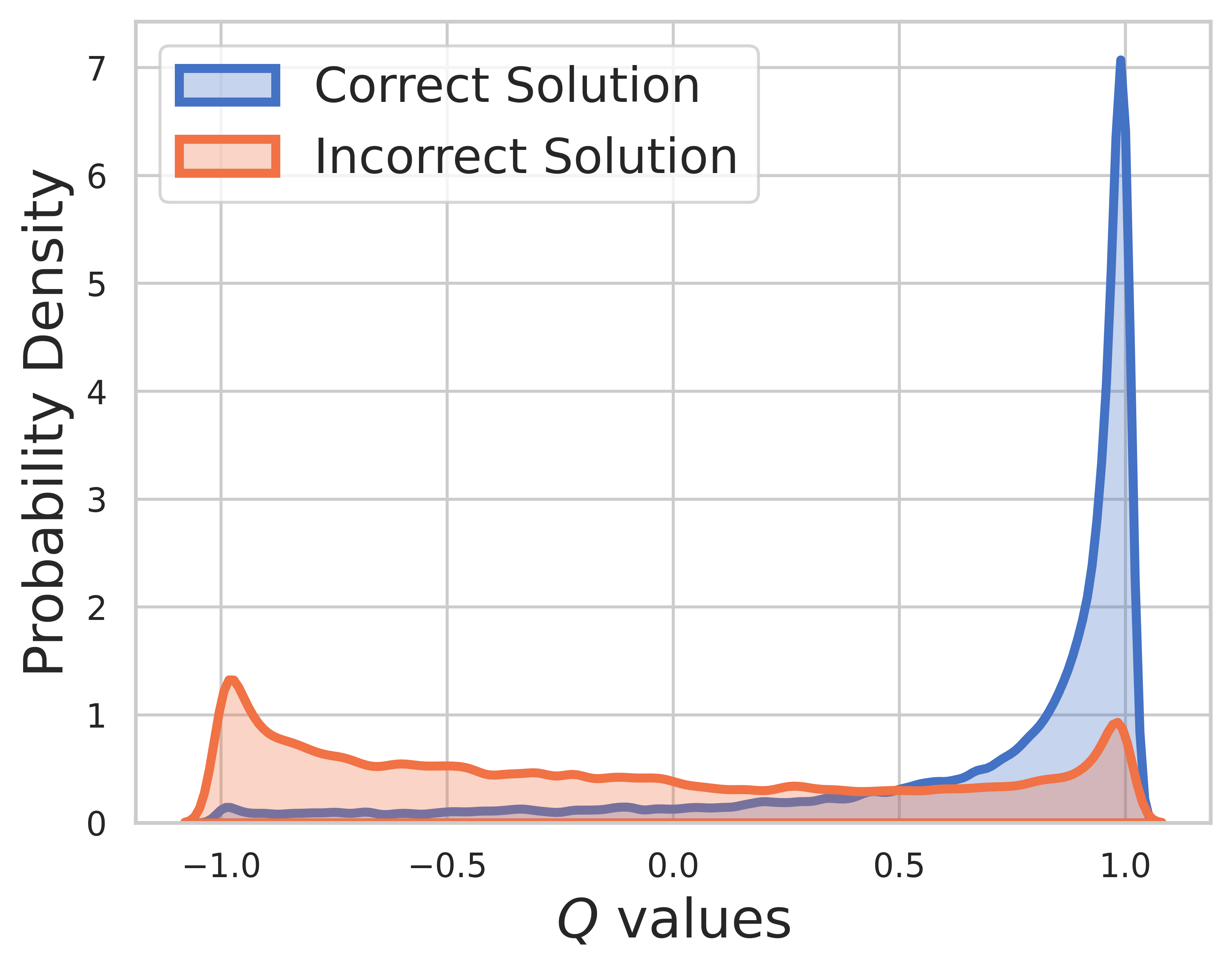
في مجموعة الاختبار، تكون الحقيقة الأساسية غير معروفة، لذا يتضمن توزيع قيمة Q خطوات متوسطة ونهائية. ومن هذا الشكل نجد
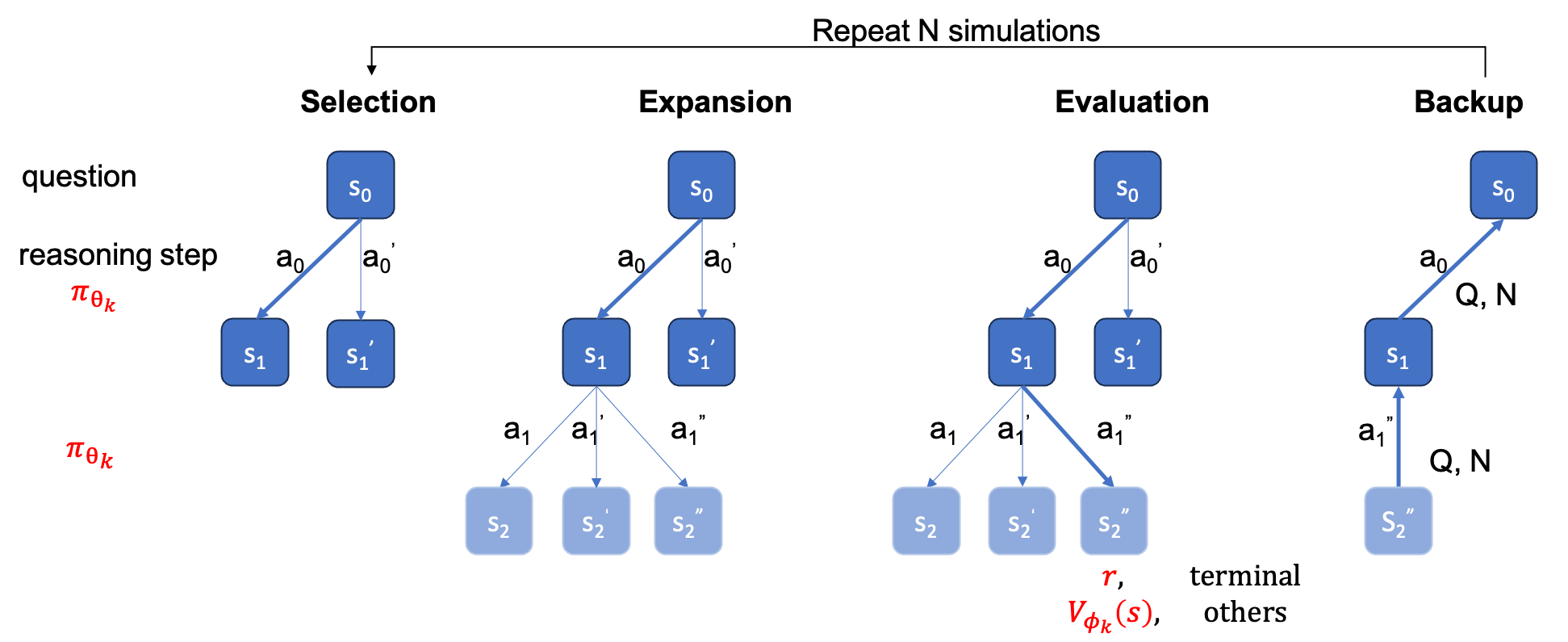
SVPO بواسطة MCTS
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
نسخة إم سي تي إس
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
مجموعة أدوات التقييم
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
إصدار OVM (نموذج قيمة النتيجة).
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}