تعد إعادة تشكيل Lanczos (تُنطق Lanchos) تقنية متطورة لاستكمال الإشارات الرقمية، مما يوفر جودة صورة فائقة مقارنة بالطرق الأبسط مثل أقرب جار والاستيفاء الثنائي الخطي. من خلال الحفاظ بشكل فعال على التفاصيل وتقليل التعرجات، يتم استخدام إعادة تشكيل Lanczos على نطاق واسع في تطبيقات معالجة الصور والإشارات.
بينما تتفوق Lanczos في جودة الصورة، إلا أن ذلك يأتي على حساب التعقيد الحسابي المتزايد. بالإضافة إلى ذلك، فإن احتمال وجود قطع أثرية "رنين"، خاصة حول الحواف الحادة، يمكن أن يكون عيبًا. على الرغم من هذه التحديات، يظل Lanczos هو الخيار المفضل لمهام مثل تغيير حجم الصورة وتدويرها نظرًا لفوائد الأداء الشامل.
توفر هذه الوثيقة نظرة عامة شاملة على إعادة أخذ العينات من Lanczos، بما في ذلك الأسس النظرية وتفاصيل التنفيذ والتطبيقات العملية. إنه بمثابة مورد قيم للمطورين والباحثين الذين يسعون إلى فهم هذه التقنية القوية واستخدامها. تتعمق الأقسام اللاحقة في الجوانب الحاسمة لإعادة تشكيل Lanczos، مثل نواة Lanczos، وعمليات الاستيفاء وإعادة التشكيل، والحفاظ على التدفق، والاختزال، والاختزال، وتحديد موضع العينة، ونطاق الإخراج، والاستيفاء متعدد الأبعاد، وقابلية الفصل. تم تضمين مثال عملي مع كود المصدر المصاحب.
نواة Lanczos، المحددة لحجم دعم معين، هي وظيفة تستخدم في إعادة تشكيل Lanczos. يتم تعريف النواة على النحو التالي:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
أين:
يتم تعريف وظيفة Sinc الطبيعية على النحو التالي:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
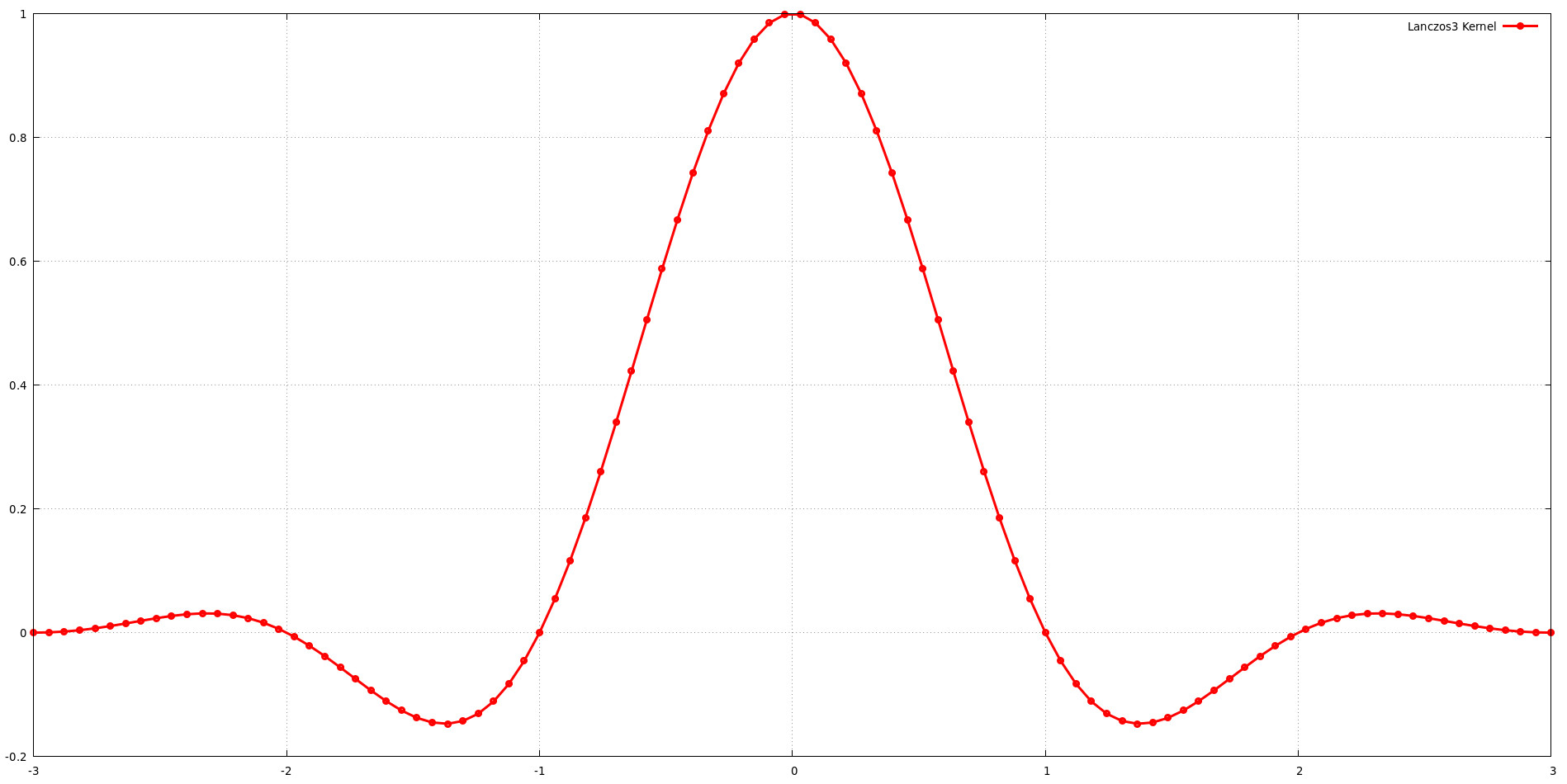
يوضح الرسم البياني شكل نواة Lanczos بحجم دعم a = 3. وهذا يعني أن النواة تتضمن ثلاثة فصوص من دالة sinc. في حين أن زيادة حجم الدعم (أ) توفر عمومًا المزيد من المرونة لتشكيل استجابة التردد، فإنها تزيد أيضًا من التكلفة الحسابية. يجب تحقيق التوازن بين جودة الصورة والكفاءة الحسابية عند اختيار حجم الدعم. إن اكتشاف جيم بلين بأن نواة Lanczos ذات = 3 توفر توازنًا ممتازًا بين الحفاظ على التردد المنخفض والرفض عالي التردد يدعم هذه الفكرة.
ملاحظة: غالبًا ما يتم استخدام المصطلحات "عرض النواة" و"حجم الدعم" و"حجم المرشح" بالتبادل لوصف المعلمة أ. ومع ذلك، في سياق إعادة تشكيل لانكزو، يعكس "حجم الدعم" المفهوم بدقة أكبر.
استيفاء Lanczos هو أسلوب يستخدم لإعادة تشكيل إشارة منفصلة إلى معدل أخذ عينات جديد. ويحقق ذلك عن طريق دمج الإشارة الأصلية مع نواة Lanczos.
يمكن حساب الإشارة المستكملة s2(x) على النحو التالي:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
أين:
الحفاظ على التدفق:
يعد عامل التطبيع w (x) أمرًا ضروريًا للحفاظ على طاقة الإشارة الإجمالية أو الكتلة أثناء عملية الاستيفاء. ويضمن أن مجموع القيم المحرفة يقارب مجموع العينات الأصلية. يتم حساب وزن الفلتر على النحو التالي:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
الاختزال:
عند زيادة معدل أخذ العينات، يمكن استخدام معادلة الاستيفاء لانكزوس مباشرة دون تعديلات.
الاختزال:
لتجنب تسمية العناصر المستعارة عند خفض معدل أخذ العينات، يجب تعديل مقياس المرشح ليتناسب مع معدل أخذ العينات الجديد.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
أين:
عند إعادة أخذ عينات إشارة من عينات n1 إلى عينات n2، يتم استخدام مواضع العينات التالية. ويستخدم المؤشر j لتمثيل العينات من الإشارة التي تم أخذ عينات منها s2(x). المصطلح (j + 0.5) هو مركز العينة في s2(x). تقوم الخطوة بتحجيم نقطة في s2(x) إلى نقطة في s1(x). الحد الأخير -0.5 في x هو تحول طور يؤدي إلى إزاحة عينات معامل Lanczos.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
عند إجراء استيفاء Lanczos، يجب توخي الحذر عند حدود الإشارة. تتضمن تقنيات التعامل مع الحواف الشائعة ما يلي:
الحشو صفر:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
لقط:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
غالبًا ما يُفضل التثبيت لأنه يقلل من آثار الحواف الناتجة عن الانقطاعات الحادة بالقرب من الحواف. ومع ذلك، يعتمد اختيار طريقة معالجة الحافة على التطبيق المحدد والإخراج المطلوب.
قد يكون نطاق s2(x) أكبر من نطاق s1(x) بسبب فصوص L(x). على سبيل المثال، يجب تثبيت إشارة الإدخال s1(x) المقابلة لألوان البكسل في النطاق [0.0,1.0] على نفس النطاق لضمان عدم تجاوز قيم الإخراج عند تحويلها مرة أخرى إلى بايت غير موقعة بقيمة [0,255] .
يمكن توسيع نواة Lanczos إلى أبعاد متعددة لإجراء الاستيفاء على الصور أو البيانات ذات الأبعاد الأعلى.
يتم تعريف نواة Lanczos ثنائية الأبعاد على النحو التالي:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
يمكن حساب الإشارة المستكملة s2(x, y) باستخدام الصيغة التالية:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
حيث w(x, y) هو عامل التطبيع المحسوب باستخدام نواة Lanczos ثنائية الأبعاد.
على عكس بعض طرق الاستيفاء، فإن نواة Lanczos غير قابلة للفصل، مما يعني أنه لا يمكن تحليلها إلى منتج حبات أحادية البعد. تؤدي هذه الخاصية بشكل عام إلى تكاليف حسابية أعلى مقارنة بالنوى القابلة للفصل. لتحسين الأداء، تقارب بعض التطبيقات نواة Lanczos عن طريق إجراء تمريرات منفصلة للأبعاد الأفقية والرأسية.
الاستيفاء الأفقي:
الاستيفاء العمودي:
التمثيل الرياضي:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
لاحظ أنه يتم حساب عوامل التطبيع w(x) وw(y) باستخدام نواة Lanczos أحادية البعد.
النقاط الرئيسية:
وبالمثل، فإن إعادة تشكيل الإشارة بشكل متكرر عدة مرات، كما يحدث عادةً لإنشاء خرائط mipmap للنسيج، يمكن أيضًا أن يؤدي إلى انخفاض جودة الصورة بسبب تراكم الأخطاء من كل خطوة لإعادة التشكيل.
قم بتشغيل مثال اختبار lancos واستخدم gnuplot لترى كيف تؤثر إعادة تشكيل Lanczos على إشارة بسيطة أحادية البعد عند تكبيرها واختزالها بعامل 2.
make
./lanczos-test
gnuplot
> load "output.plot"
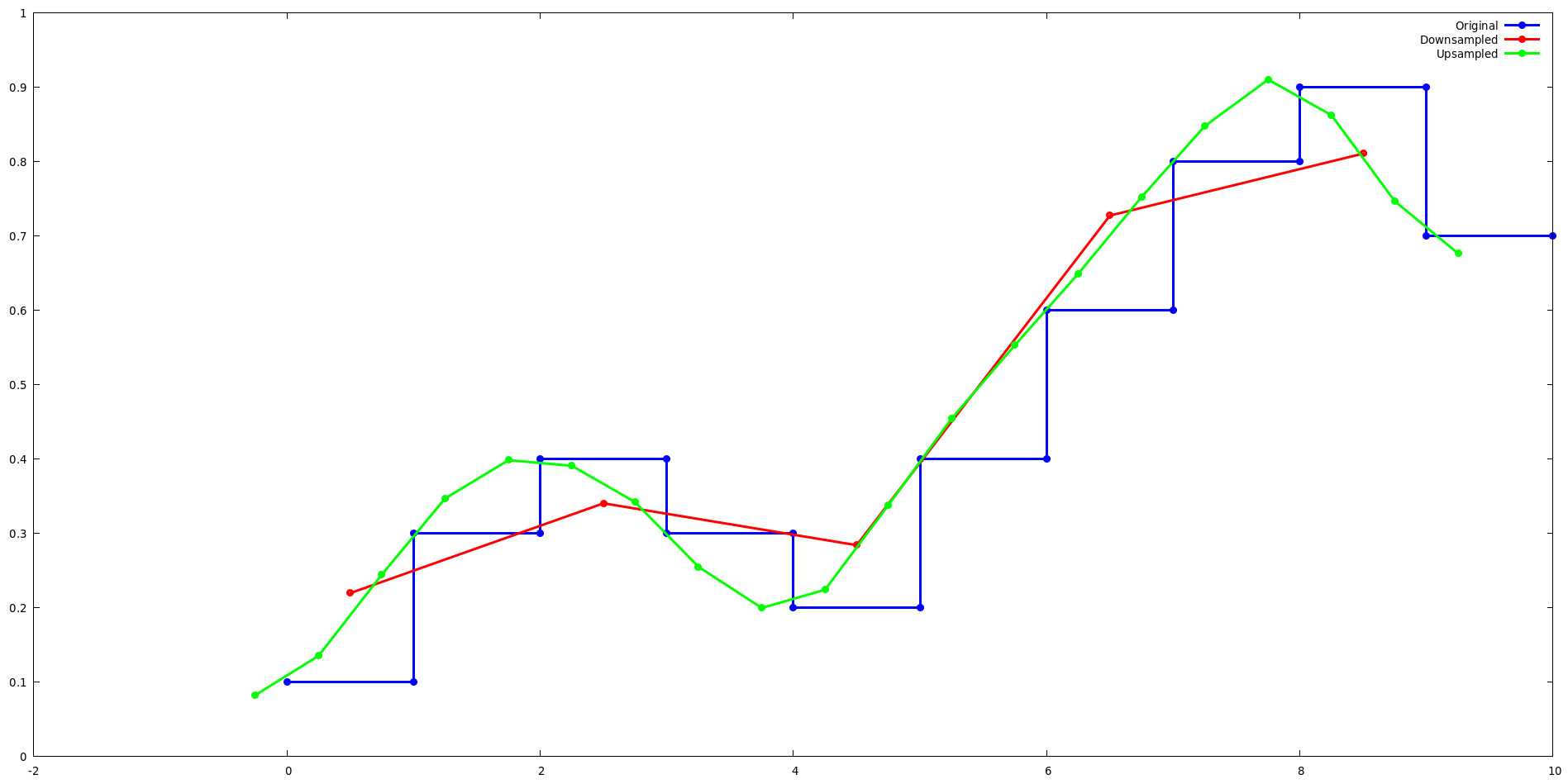
الاختزال:
عند الاختزال بقوة اثنين، تتنقل نواة Lanczos بين مجموعات من القيم ذات مستوى 2^. على سبيل المثال، ضع في اعتبارك المخرجات الأربعة الأولى من المثال النموذجي لاختبار Lanzcos. لاحظ أن مخرجات L(x) تتكرر لـ j={0,2} وj={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
الاختزال:
عند الاختزال بقوة اثنين، تصبح نواة Lanczos مستقلة عن x لأن (x - Floor(x)) تصبح ثابتًا يطابق تحول الطور. على سبيل المثال، ضع في اعتبارك أول مخرجين من مثال الاختزال لاختبار Lanzcos. لاحظ أن مخرجات L(x) تتكرر لكل j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
وكتحسين إضافي، قد يتم حساب نواة Lanczos مسبقًا لهذه الحالات للتخلص من حساب دالة المزامنة الباهظة الثمن.
تم إنشاء هذا الملف التمهيدي بمساعدة Google Gemini.
تشمل المراجع الإضافية ما يلي:
تم تنفيذ هذا الكود بواسطة Jeff Boody بموجب ترخيص MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.