python kmeans

بيثون كمين

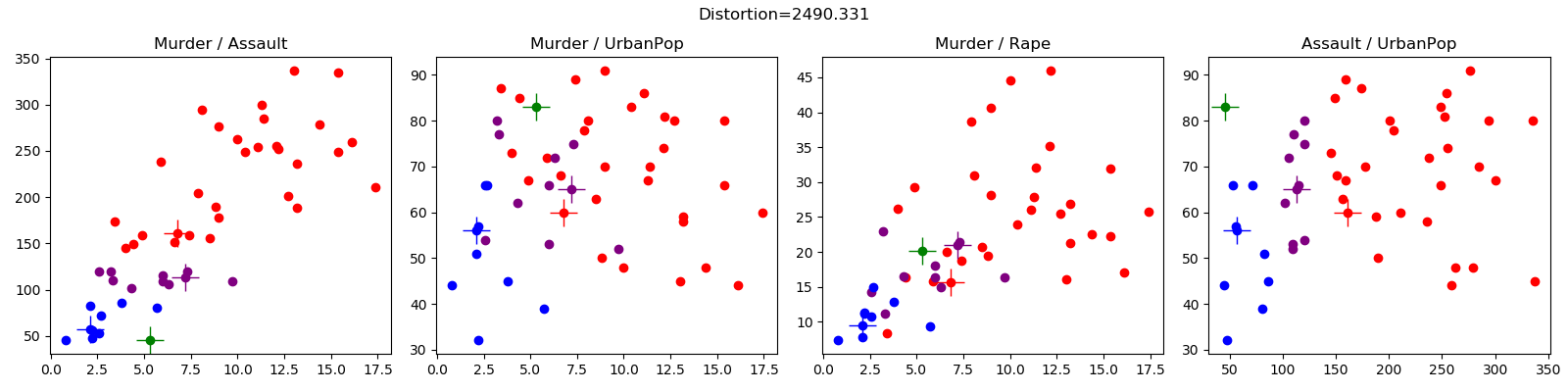
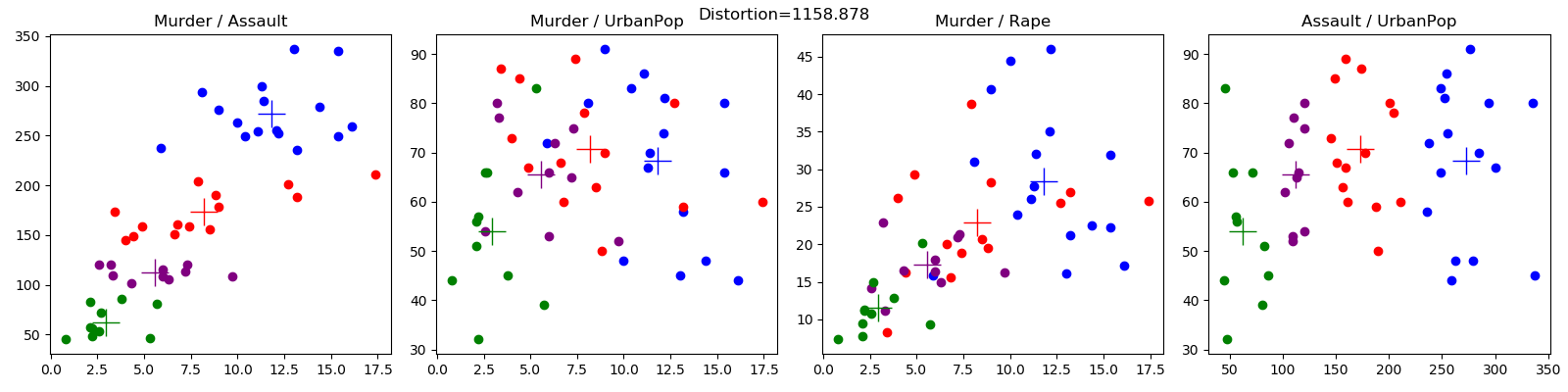
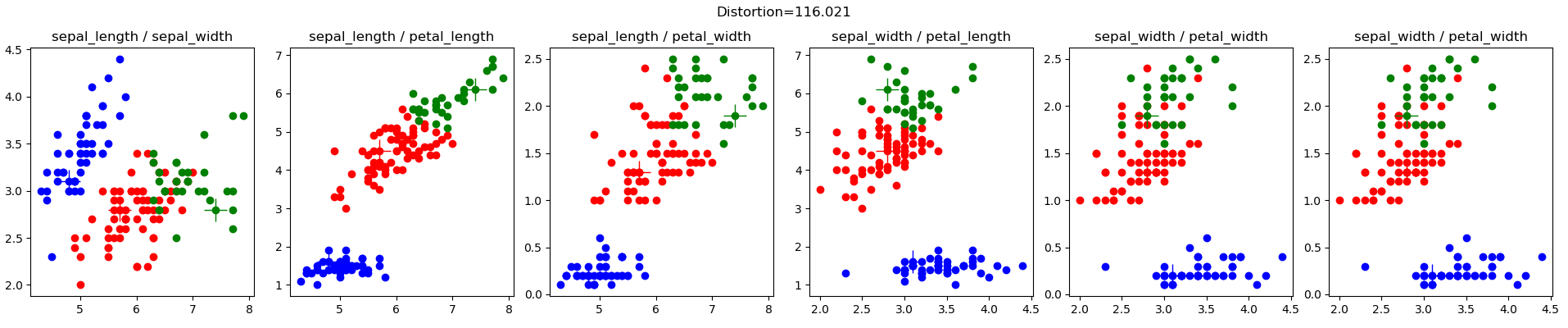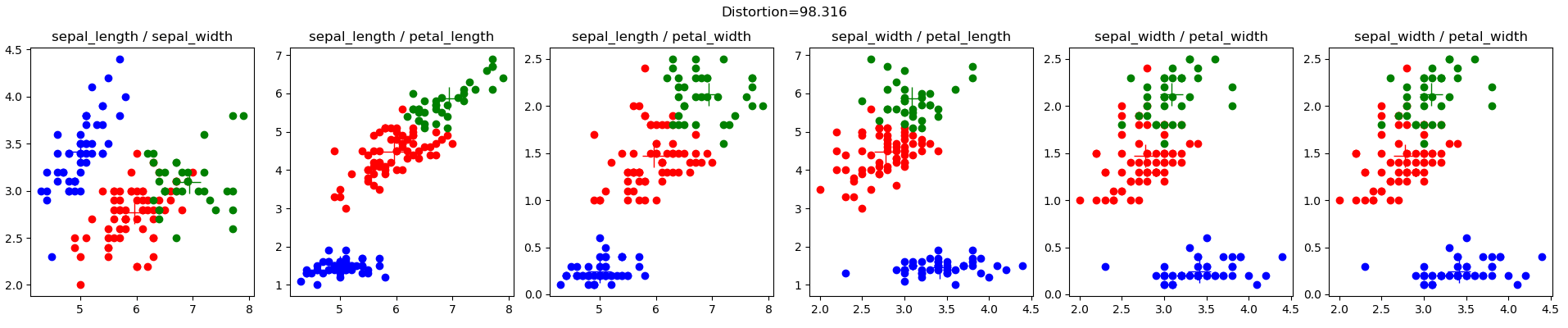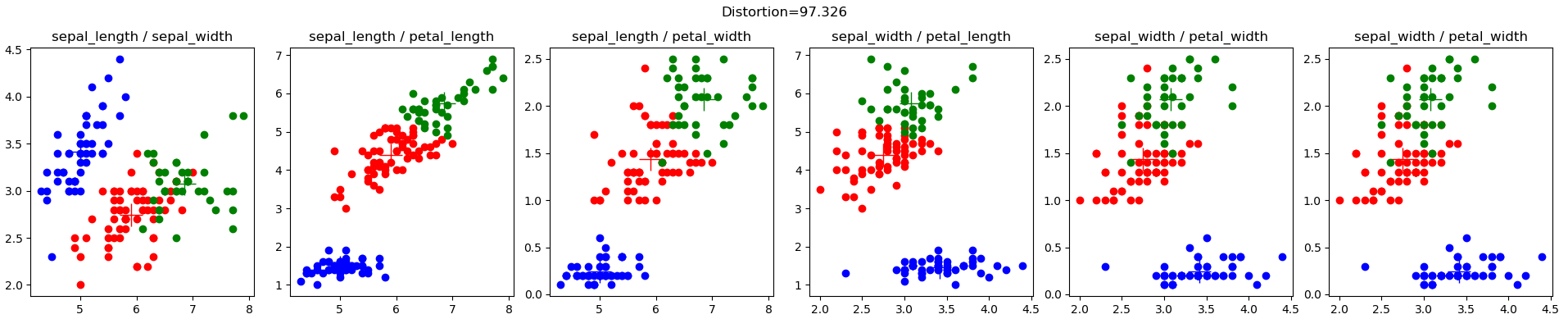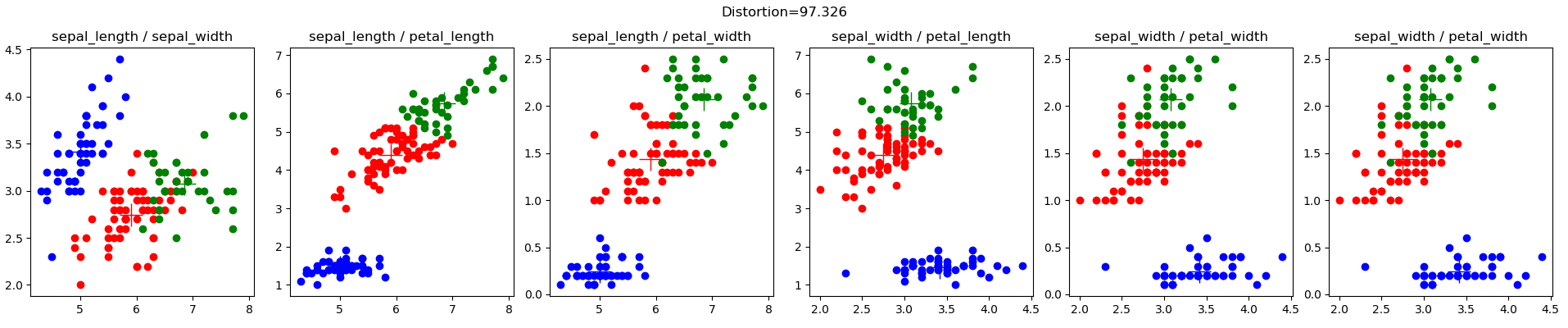
تنفيذ بايثون للمجموعات k. k-means هي تقنية تعلم غير خاضعة للرقابة تحاول تجميع نقاط بيانات متشابهة معًا في عدد محدد من المجموعات بواسطة المستخدم. يوضح المثال أدناه تقدم المجموعات لمجموعة بيانات Iris باستخدام خوارزمية تهيئة النقطه الوسطى k-means++.

وصف

تعني k محاولات تحديد مستخدم محدد لعدد k (<N) من المجموعات من مجموعة من المتجهات ذات القيمة الحقيقية ذات الأبعاد N. تستمر الخوارزمية بمحاولة تقليل مجموع المسافات المربعة من مركز المجموعة إلى أعضاء المجموعة. تستمر الخوارزمية الأساسية في ثلاث مراحل:

1. تهيئة النقط الوسطى العشوائية (مراكز الكتلة) ؛
2. تعيين نقاط البيانات إلى أقرب مجموعة وفقا لقياس المسافة (عادة المسافة الإقليدية)؛
3. تحديث النقط الوسطى إلى متوسط ​​أعضاء الكتلة؛
4. كرر الخطوتين 2 و3 حتى لا تتغير المهام من الخطوة 2.

إخراج الخوارزمية عبارة عن تعيين كتلة لكل نقطة بيانات، ومستوى نهائي من "التشويه". لا تنتج الخوارزمية حلاً مثاليًا يمكن إثباته، وقد تتسبب مراكز المجموعة الأولية في تعطل الخوارزمية في الحل الأمثل محليًا والذي من الواضح أنه دون المستوى الأمثل (راجع المثال الأساسي ثنائي الأبعاد في قسم النتائج).

لقد ركزت الكثير من الأبحاث على:

• اختيار مراكز الكتلة الأولية. K-Means++ هي طريقة معروفة، وهي متضمنة في هذا التنفيذ، والخوارزمية موضحة في القسم الفرعي التالي.
• حساب المسافات، أي استخدام مقاييس أخرى غير الإقليدية انظر هنا.

K-يعني ++

بدلاً من تهيئة النقط الوسطى العشوائية كما في الخطوة 1 أعلاه، k-means++ ينشر احتماليًا النقط الوسطى الأولية لتجنب التكوين الأولي السيئ، الخوارزمية هي:

1. اختر النقطه الوسطى الأولى بشكل عشوائي.
2. لكل نقطة بيانات x، احسب المسافة d(x)، من x إلى أقرب نقطة مركزية تم اختيارها بالفعل.
3. حدد نقطة بيانات لتكون النقطه الوسطى التالية باستخدام احتمال مرجح يتناسب مع d(x)2.

تعطي هذه التقنية الأفضلية لنقاط البيانات التي ليست قريبة من النقط الوسطى الأولية الأخرى، وتستخدم سياسة اختيار تذكرنا باختيار عجلة الروليت (أو اللياقة البدنية المتناسبة) الذي غالبًا ما يستخدم في الخوارزميات الجينية.

موارد

الخوارزمية الأساسية

• تم وصف K-Means في أفضل 10 خوارزميات لاستخراج البيانات؛

• تم توضيح وسائل K-Means في نظرية المعلومات والاستدلال وخوارزميات التعلم، مقتطف منها هنا؛

• البروفيسور أندرو مور من CMU لديه بعض الملاحظات الجيدة هنا؛

• مثال Edureka، باستخدام بيانات الجريمة

تهيئة المجموعات

• K-Means++، والورقة الكاملة هنا

• دراسة مقارنة لطرق التهيئة الفعالة لخوارزمية التجميع K-Means

لماذا لا تستخدم SciPy؟

لدى SciPy تطبيق k-means. الهدف من هذا العمل هو بناء تطبيق بايثون خالص لأغراض التعلم ومساعدة الآخرين على تعلم خوارزمية k-means. سيتمكن القراء المهتمون الذين لديهم الحد الأدنى من الخبرة في لغة بايثون من قراءة هذا الرمز وتخطيه دون التعقيد الإضافي لمكتبة مثل SciPy. ليس بأي حال من الأحوال مخصص للاستخدام الإنتاجي :)

تشغيل الكود

التبعيات

• بيثون 3.6.3
• matplotlib 2.1.1 - انظر هنا للحصول على تعليمات التثبيت.

تنفيذ

قم بتشغيل الكود باستخدام مترجم بايثون:

python kmeans.py ./resources/<config.cfg>

حيث config.cfg هو ملف تكوين نص عادي. تنسيق ملف التكوين هو إملاء بايثون مع الحقول التالية:

 {
   'data_file' : '\resources\iris.csv',
   'data_project_columns' : ['sepal_length','sepal_width','petal_length','petal_width','class'],
   'k' : 3,
   'cluster_atts' : ['sepal_length','sepal_width','petal_length','petal_width'],
   'init_cluster_func' : 'kmeans_plus_plus',
   'plot_config' :
    {'output_file_prefix' : 'iris',
     'plots_configs': [
        {'plot_atts' : ['sepal_length','sepal_width']},
        {'plot_atts' : ['sepal_length','petal_length']},
        {'plot_atts' : ['sepal_length','petal_width']},
        {'plot_atts' : ['sepal_width','petal_length']},
        {'plot_atts' : ['sepal_width','petal_width']},
        {'plot_atts' : ['sepal_width','petal_width']}
     ]
   }
}

عليك أن تحدد:

• ملف بيانات CSV؛
• مجموعة فرعية من الحقول لعرضها من الملف؛
• عدد العناقيد المراد تشكيلها، ك؛
• المجموعة الفرعية من السمات المستخدمة في عملية التجميع؛
• حدد بشكل اختياري وظيفة المجموعة الأولية (افتراضي = 'rand_init_centroids')، قام المؤلفون المهتمون بإضافة خاصيتهم إلى الكود وتحديده هنا؛
• تكوين المؤامرة الذي يتضمن
  • بادئة لملفات png التي تم إنشاؤها أثناء العملية في دليل العمل، إذا لم يتم تحديد ذلك، فلن يتم إنتاج الصور؛
  • تكوينات قطعة الأرض الفردية، تقتصر على بعدين لكل قطعة أرض.

نتائج

مجموعة بيانات القزحية

مجموعة بيانات Iris (iris.config)، من Lichman, M. (2013). مستودع التعلم الآلي UCI. إيرفاين، كاليفورنيا: كلية المعلومات وعلوم الكمبيوتر بجامعة كاليفورنيا، هي مجموعة بيانات معروفة جدًا في مجتمع التعلم الآلي. فيما يلي نتائج مجموعاتي الأولية العشوائية:

البيانات الاصطناعية الأساسية ثنائية الأبعاد

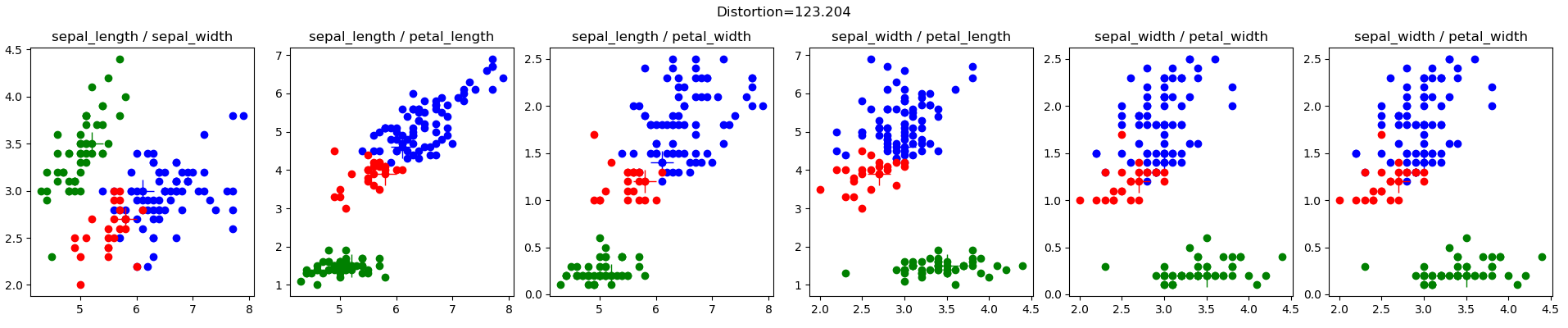
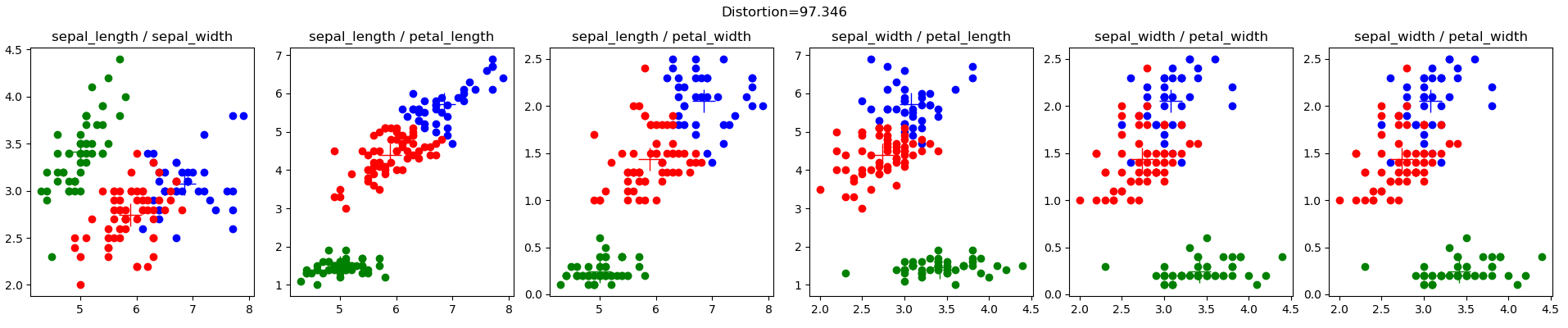
تم إنشاء هذه البيانات لأغراض تصحيح الأخطاء (راجع basic2d.config)، وهي توضح تأثير الاختيار السيئ للمجموعات العشوائية الأولية. توضح النتائج أدناه تكوينًا أوليًا للنقطه الوسطى يمنع الخوارزمية من الوصول إلى مهمة المجموعة الواضحة. في هذه الحالة، يعني موضع النقطه الوسطى الحمراء أن النقطه الوسطى الزرقاء تلتقط جميع نقاط البيانات في الربعين السفلي الأيسر والأيمن السفلي.

جريمة

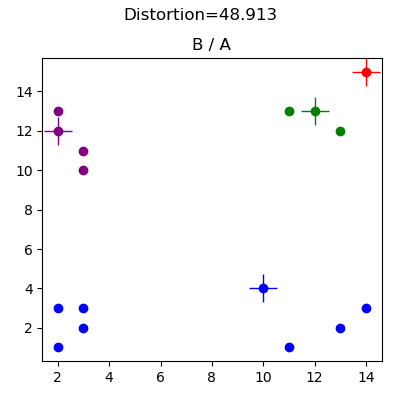
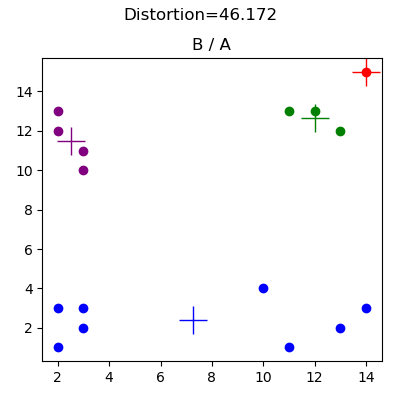
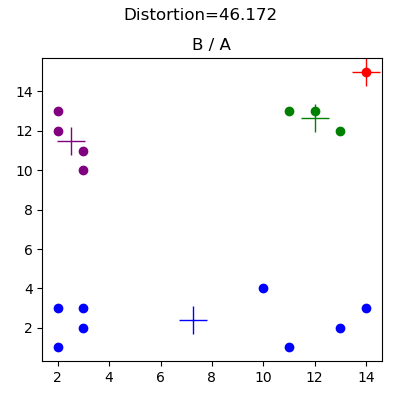
مجموعة بيانات الجريمة (crime.config) مأخوذة من Edureka، هنا.