وتفكيك السلسلة الزمنية يعني فصلها إلى مكوناتها المكونة، والتي عادة ما تكون مكون اتجاه ومكون غير منتظم، وإذا كانت سلسلة زمنية موسمية، فهي مكون موسمي. بالنسبة لمعلومات سهم TSLA، من مخطط اتجاه السعر، يمكننا أن نرى أنه لا يوجد مكون موسمي داخل البيانات. ولكن يجب أن تتضمن بيانات السلاسل الزمنية هذه عنصرًا للاتجاه ومكونًا غير منتظم. يتضمن تحليل السلسلة الزمنية محاولة فصل السلسلة الزمنية إلى هذه المكونات، أي تقدير مكون الاتجاه والمكون غير المنتظم. سنقوم بوظيفة SMA() لتسهيل بيانات TSLA. سوف نختار الترتيب المختلف (n=8 وn=40) للتحقق من مكون الاتجاه. الهدف هو أن نحاول تسهيل البيانات باستخدام متوسط حركة بسيط.
نموذج أريما
ARIMA (المتوسط المتحرك المتكامل التلقائي) هو أداة رئيسية تستخدم في تحليل السلاسل الزمنية لمحاولة التنبؤ بالقيم المستقبلية للمتغير بناءً على قيمته الحالية. معادلة التنبؤ ARIMA(p,d,q): نماذج ARIMA هي، من الناحية النظرية، الفئة الأكثر عمومية من النماذج للتنبؤ بسلسلة زمنية والتي يمكن جعلها "ثابتة" عن طريق الاختلاف. يتم تعريف نماذج ARIMA للسلاسل الزمنية الثابتة. لذلك، إذا بدأت بسلسلة زمنية غير ثابتة، فسوف تحتاج أولاً إلى "تمييز" السلسلة الزمنية حتى تحصل على سلسلة زمنية ثابتة. لتمييز السلاسل الزمنية d مرات للحصول على سلسلة ثابتة، نستخدم الدالة diff(). بعد ذلك سوف نستخدم اختبار ADF الرسمي الذي لا يرفض الفرضية الصفرية لعدم الاستقرار، مما يؤكد فحصنا البصري:
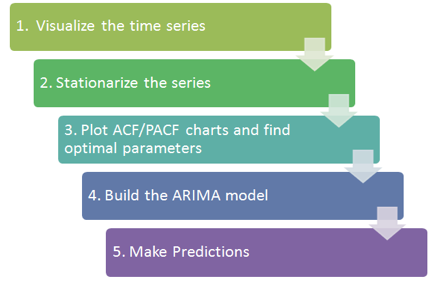
في هذا القسم، نستخدم بيانات سهم TESLA كسلسلة زمنية. نحن نحللها ونستخدم التجانس الأسي HoltWinter وARIMA للتنبؤ بسعر السهم المستقبلي. الإجراءات الأساسية هي كما في الشكل التالي.
والشيء الآخر هو أنه يجب علينا دائمًا تحليل الأخطاء وضبط معلمات النموذج لتحقيق نتائج أفضل.