يتيح لك greta.gam استخدام وظائف mgcv الأكثر سلاسة وبناء جملة الصيغة لتحديد المصطلحات السلسة للاستخدام في نموذج greta. يمكنك بعد ذلك تحديد احتمالية إكمال النموذج وملاءمته بواسطة MCMC.
هذا هو العمل الجاري!
فيما يلي مثال بسيط مقتبس من ملف المساعدة mgcv ?gam :
في mgcv :
library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )
# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model
# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat ) الآن تركيب نفس النموذج في greta :
library( greta.gam )
# > Loading required package: greta
# >
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# >
# > binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# >
# > %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# > eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# > tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!
# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )
# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))
# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )
# build model
m <- model( z_pred )
# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#> warmup 0/1000 | eta: ?s warmup == 50/1000 | eta: 30s warmup ==== 100/1000 | eta: 17s warmup ====== 150/1000 | eta: 12s warmup ======== 200/1000 | eta: 10s warmup ========== 250/1000 | eta: 8s warmup =========== 300/1000 | eta: 7s warmup ============= 350/1000 | eta: 6s warmup =============== 400/1000 | eta: 5s warmup ================= 450/1000 | eta: 5s warmup =================== 500/1000 | eta: 4s warmup ===================== 550/1000 | eta: 4s warmup ======================= 600/1000 | eta: 3s warmup ========================= 650/1000 | eta: 3s warmup =========================== 700/1000 | eta: 2s warmup ============================ 750/1000 | eta: 2s warmup ============================== 800/1000 | eta: 1s warmup ================================ 850/1000 | eta: 1s warmup ================================== 900/1000 | eta: 1s warmup ==================================== 950/1000 | eta: 0s warmup ====================================== 1000/1000 | eta: 0s
# > sampling 0/200 | eta: ?s sampling ========== 50/200 | eta: 1s sampling =================== 100/200 | eta: 0s sampling ============================ 150/200 | eta: 0s sampling ====================================== 200/200 | eta: 0s
# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])
# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL
# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )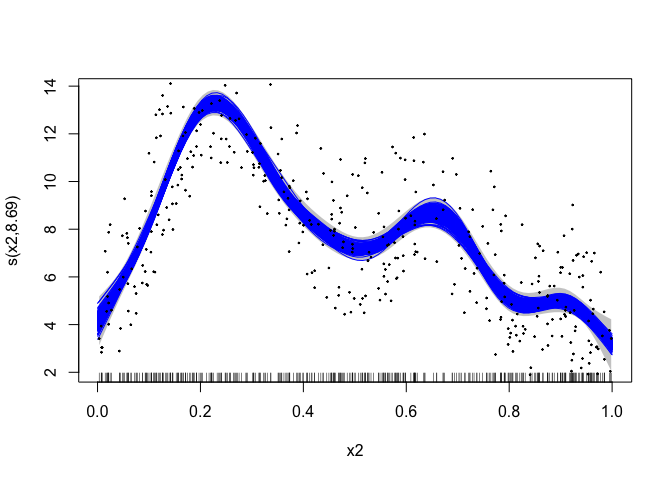
يستخدم greta.gam بعض الحيل من روتين jagam (Wood, 2016) في mgcv لتفعيل الأمور. فيما يلي بعض التفاصيل المختصرة للمهتمين بالأعمال الداخلية...
تعد GAMs نماذج ذات تفسيرات بايزي (حتى عند تركيبها باستخدام أساليب "متكررة"). يمكن للمرء أن يفكر في مصفوفة الجزاء الأكثر سلاسة كمصفوفة دقة سابقة في نموذج التأثيرات العشوائية الافتراضية. يتم إنشاء مصفوفات التصميم تمامًا كما في الحالة المتكررة. انظر ميلر (2021) لمزيد من المعلومات حول هذا الموضوع.
هناك صعوبة طفيفة في التفسير البايزي لـ GAM، حيث أن الأقدمية، في شكلها الساذج، غير مناسبة باعتبارها الفضاء الفارغ للعقوبة (في الحالة 1D، عادةً ما يكون المصطلح الخطي). للحصول على الأسبقية المناسبة، يمكننا استخدام إحدى "الحيل" المستخدمة في Marra & Wood (2011) - وهي معاقبة أجزاء العقوبة التي تؤدي إلى الأسبقية غير الصحيحة بطريقة أو بأخرى. نحن نأخذ الخيار الذي يقدمه jagam وننشئ مصفوفة جزاء إضافية لهذه الشروط (من التحليل الذاتي لمصفوفة الجزاء؛ انظر Marra & Wood, 2011).
Marra، G and Wood، SN (2011) اختيار متغير عملي للنماذج المضافة المعممة. الإحصاء الحسابي وتحليل البيانات، 55، 2372-2387.
ميلر دي إل (2021). وجهات النظر بايزي للنمذجة المضافة المعممة. arXiv.
Wood، SN (2016) مجرد نموذج آخر لإضافات Gibbs: التواصل بين JAGS و mgcv. مجلة البرمجيات الإحصائية 75، العدد. 7