Dropout NeuralNetworks
1.0.0
في هذا المشروع البحثي، سأركز على تأثيرات تغير معدلات التسرب على مجموعة بيانات MNIST. هدفي هو إعادة إنتاج الشكل أدناه مع البيانات المستخدمة في ورقة البحث. الغرض من هذا المشروع هو معرفة كيفية إنتاج رقم التعلم الآلي. وعلى وجه التحديد، التعرف على تأثيرات خطأ التصنيف عند تغيير/عدم تغيير احتمالية التسرب.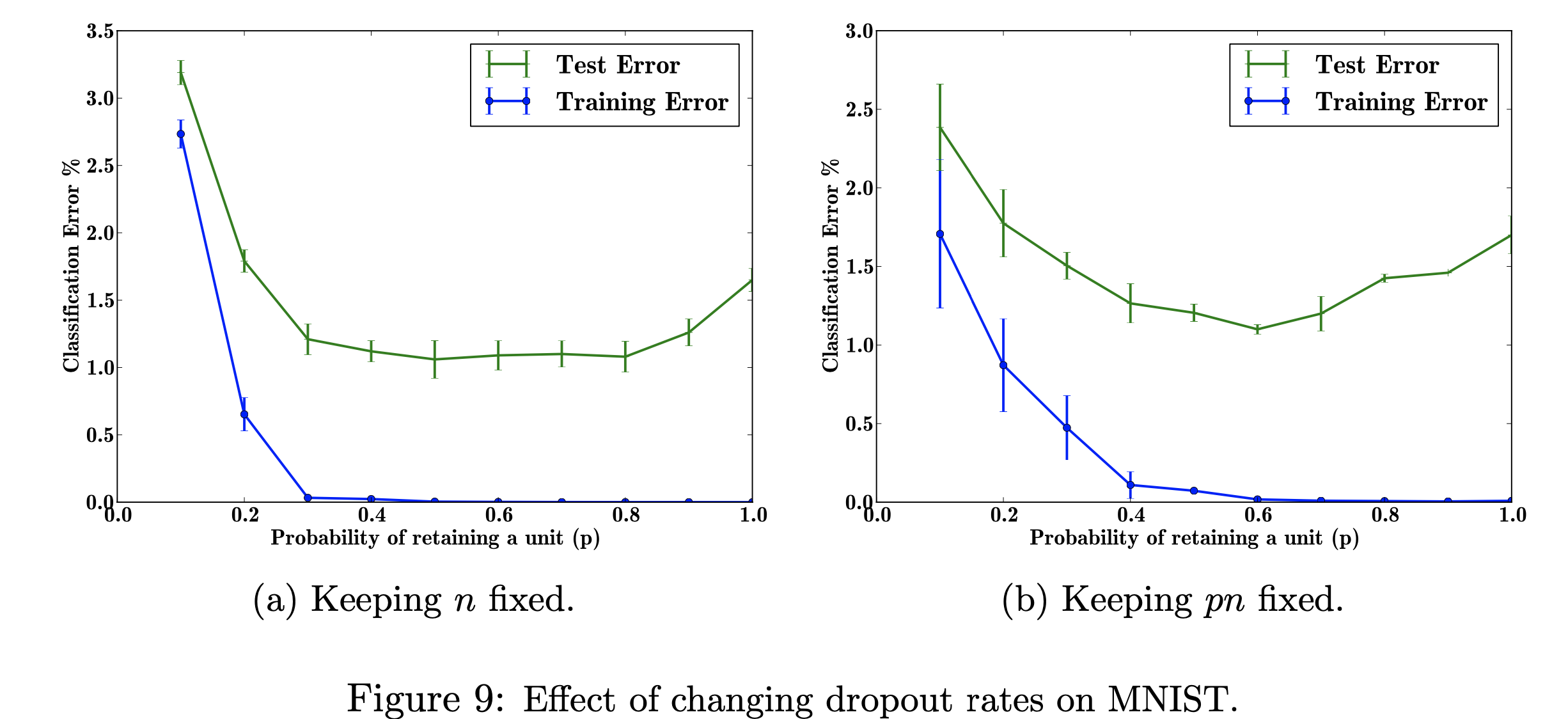
الشكل مشار إليه من: Srivastava, N., Hinton, G.,Krizhevsky, A., Krizhevsky, I., Salakhutdinov, R., التسرب: طريقة بسيطة لمنع الشبكات العصبية من التجاوز، الشكل 9
لقد استخدمت TensorFlow لتشغيل التسرب على مجموعة بيانات MNIST، واستخدمت Matplotlib للمساعدة في إعادة إنشاء الشكل في الورقة. لقد استخدمت أيضًا مكتبة عشرية مدمجة لحساب القيم المختلفة لـ p، من 0.0 إلى 1.0. تم استيراد المكتبة "csv" لإضافة بيانات تم تشغيلها مسبقًا إلى ملف CSV، لتوفير الوقت في حساب القيم المحسوبة بالفعل لـ p. تم استيراد Numpy للحصول على نفس حجم الخطوة على المحورين x وy. أخيرًا، قمت باستيراد "نظام التشغيل" حتى أتمكن من التخلص من الخطأ الناتج عن استخدام وحدة المعالجة المركزية (CPU) بدلاً من وحدة معالجة الرسومات (GPU).
استكشاف تأثيرات القيم المتغيرة للمعلمة الفائقة القابلة للضبط 'p' (احتمال الاحتفاظ بوحدة في الشبكة) وعدد الطبقات المخفية، 'n'، التي تؤثر على معدلات الخطأ. عندما يكون حاصل ضرب p وn ثابتًا، يمكننا أن نرى أن حجم الخطأ للقيم الصغيرة لـ p قد انخفض (الشكل 9 أ) مقارنة بالحفاظ على عدد الطبقات المخفية ثابتًا (الشكل 9 ب).
مع بيانات التدريب المحدودة، فإن العديد من العلاقات المعقدة بين المدخلات/المخرجات ستكون نتيجة لضوضاء أخذ العينات. وسوف تكون موجودة في مجموعة التدريب، ولكن ليس في بيانات الاختبار الحقيقية حتى لو تم استخلاصها من نفس التوزيع. يؤدي هذا التعقيد إلى التجاوز، وهذه إحدى الخوارزميات التي تساعد في منع حدوث ذلك. المدخلات لهذا الشكل عبارة عن مجموعة بيانات من الأرقام المكتوبة بخط اليد، والإخراج بعد إضافة التسرب عبارة عن قيم مختلفة تصف نتيجة تطبيق طريقة التسرب. بشكل عام، يكون الخطأ أقل بعد إضافة التسرب.
إحدى مشكلات العالم الحقيقي التي يمكن أن ينطبق عليها ذلك هي البحث على Google، فقد يبحث شخص ما عن عنوان فيلم ولكنه قد يبحث فقط عن الصور لأنه متعلم أكثر بصريًا. لذا فإن حذف الأجزاء النصية، أو الشروحات الموجزة سيساعدك على التركيز على ميزات الصورة. تنص المقالة على مكان استرداد البيانات من (http://yann.lecun.com/exdb/mnist/). كل صورة عبارة عن تمثيل 28 × 28 رقمًا. يبدو أن التسميات y هي أعمدة بيانات الصورة.
هدفي في إعادة إنتاج هذا الرقم هو اختبار/تدريب البيانات وحساب خطأ التصنيف لكل احتمال p (احتمال الاحتفاظ بوحدة في الشبكة). هدفي هو زيادة p مع انخفاض الخطأ لإظهار أن التنفيذ الخاص بي صالح، وسوف أقوم بضبط هذه المعلمة المفرطة للحصول على نفس النتيجة. سأفعل ذلك من خلال تكرار جميع بيانات التدريب والاختبار باستخدام بنية 784-2048-2048-2048-10 والحفاظ على n ثابتًا ثم تغيير pn ليتم إصلاحه. سأقوم بعد ذلك بجمع/كتابة البيانات في ملف CSV. سيحتوي ملف CSV هذا بعد ذلك على جميع البيانات اللازمة لإخراج الأرقام. في هذا المشروع، سوف أتعلم كيف يمكن لمعدل التسرب أن يفيد الخطأ الإجمالي في الشبكة العصبية.
انقر للعرض
