rodeo

مسابقات رعاة البقر: حلال ODE الاحتمالي السريع

الصفحة الرئيسية | التثبيت | التوثيق | البرنامج التعليمي | المطورين

---

وصف

Rodeo هي مكتبة Python سريعة تستخدم الأرقام الاحتمالية لحل المعادلات التفاضلية العادية (ODEs). أي أن معظم أدوات حل ODE (مثل طريقة أويلر) تنتج تقريبًا حتميًا لـ ODE على شبكة بحجم الخطوة $دلتا تي$ . مثل $دلتا تي$ عندما يذهب إلى الصفر، يتقارب التقريب مع حل ODE الحقيقي. تقوم الحلول الاحتمالية أيضًا بإخراج الحل على شبكة ذات حجم $دلتا تي$ ; ومع ذلك، فإن الحل عشوائي. لا يزال، كما $دلتا تي$ إذا ذهبت إلى الصفر، فإن التقريب العددي الاحتمالي يتقارب مع الحل الحقيقي.

توفر مسابقات رعاة البقر مجموعة تقريبية خفيفة الوزن وقابلة للتوسيع لنموذج الترشيح البايزي غير الخطي الشائع لدى العديد من المحللين الاحتماليين (Tronarp et al (2018)). يبدأ ذلك بوضع عملية Gaussian مسبقًا على حل ODE، وتحديثها بشكل تسلسلي أثناء خطوات الحل عبر الشبكة. تم بناء مسابقات رعاة البقر على جاكس الذي يسمح بالتجميع والتمايز التلقائي في الوقت المناسب. واجهة برمجة التطبيقات الخاصة بـ jax تعادل تقريبًا واجهة numpy .

توفر مسابقات رعاة البقر أداتين رئيسيتين: واحدة لتقريب حل ODE والأخرى لاستدلال المعلمات. بالنسبة للسابق نقدم:

• solve : تنفيذ حل ODE الاحتمالي الذي يستخدم نموذج تصفية بايزي غير الخطي.

بالنسبة للأخير نقدم طرق تقريب الاحتمالية:

• basic : تنفيذ طريقة تقريب الاحتمالية الأساسية (يمكن العثور على التفاصيل في Wu and Lysy (2023)).
• fenrir : تنفيذ فنرير (ترونارب وآخرون (2022)).
• marginal_mcmc : تنفيذ MCMC لطريقة Chkrebtii (Chkrebtii et al (2016)).
• dalton : تنفيذ تقريب احتمالية ODE المتكيف مع البيانات (Wu and Lysy (2023)).

يمكن العثور على أمثلة تفصيلية لاستخدامها في قسم الوثائق. يرجى ملاحظة أن هذه هي نسخة جاكس فقط من مسابقات رعاة البقر . بالنسبة للإصدارات القديمة التي تستخدم واجهات خلفية أخرى مختلفة، يرجى الاطلاع هنا.

تثبيت

قم بتنزيل الريبو من GitHub ثم قم بالتثبيت باستخدام البرنامج النصي setup.cfg :

git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . 

التوثيق

يرجى الانتقال أولاً إلى readthedocs للاطلاع على الوثائق المقدمة للأمثلة التالية.

• برنامج تعليمي سريع حول حل مشكلة ODE بسيطة.

• مثال لحل ODE ذات الترتيب الأعلى.

• مثال لحل قصيدة فوضوية صعبة.

• مثال على مشكلة استنتاج المعلمة حيث نستخدم تقريب لابلاس.

تجول

في هذه الإرشادات التفصيلية، نعرض كيفية حل ODE باستخدام الحل الاحتمالي الخاص بنا واستدلال معلمة السلوك. سنقوم أولاً بتوضيح الإعداد لحل ODE. ولتحقيق هذه الغاية، دعونا نفكر في مثال ODE المرتب أولاً (نموذج FitzHugh-Nagumo )،

$$ begin{align*} frac{dV}{dt} &= c(V - frac{V^3}{3} + R)، \ frac{dR}{dt} &= - فارك {(V - a - bR)} {c}، \ X(t) &= (V(0)، R(0)) = (-1,1). end{محاذاة*} $$

حيث الحل $X(ر)$ سعى على الفاصل الزمني $t في [0, 40]$ و $ثيتا = (أ، ب، ج) = (.2،.2،3)$ .

بعد ملاحظة (وو وليسي (2023))، لدينا $p-1=1$ في هذا المثال. لتقريب الحل باستخدام الحل الاحتمالي، نستخدم عملية غوسية بسيطة اقترحها سابقًا Schober et al (2019)؛ وهي ذلك $V(ر)$ و $R(ر)$ مستقلة $س-1$ مرات الحركة البراونية المتكاملة، من هذا القبيل

$$ begin{المعادلة*} x^{(q)}(t) = sigma_x B(t) end{المعادلة*} $$

ل $x=V، R$ . والنتيجة هي أ $س$ عملية ماركوف غاوسية الأبعاد المستمرة $boldsymbol{x(t)} = big(x^{(0)}(t), x^{(1)}(t), ldots, x^{(q-1)}(t) كبير)$ لكل متغير $x=V، R$ . هنا $x^{(ط)}(ر)$ يدل على $i$ - المشتقة من $x(ر)$ . يحدد نموذج IBM أن كلاً من هذه العناصر مستمر، ولكن $x^{(ف)}(ر)$ ليس كذلك. ولذلك، علينا أن نختار $q geq p$ . عادة ما تكون فكرة جيدة أن تمتلكها $س$ أكبر قليلا من $p$ وخاصة عندما نعتقد أن الحل الحقيقي $X(ر)$ على نحو سلس. ومع ذلك، زيادة $س$ يزيد أيضًا العبء الحسابي، وليس من الضروري أن يكون كبيرًا حتى يعمل الحل. في هذا المثال سوف نستخدم $س=3$ . للتهيئة، نقوم ببساطة بتعيين $boldsymbol {X(0)} = (V^{(0)}(0)، V^{(1)}(0)، 0، R^{(0)}(0)، R^{( 1)}(0)، 0)$ حيث قمنا بحشو القيمة الأولية بالأصفار للمشتق الأعلى. كود بايثون لتنفيذ كل هذا هو كما يلي.

 import jax
import jax . numpy as jnp
import rodeo

def fitz_fun ( X , t , ** params ):
    "FitzHugh-Nagumo ODE in rodeo format."
    a , b , c = params [ "theta" ]
    V , R = X [:, 0 ]
    return jnp . array (
        [[ c * ( V - V * V * V / 3 + R )],
         [ - 1 / c * ( V - a + b * R )]]
    )

def fitz_init ( x0 , theta ):
    "FitzHugh-Nagumo initial values in rodeo format."
    x0 = x0 [:, None ]
    return jnp . hstack ([
        x0 ,
        fitz_fun ( X = x0 , t = 0. , theta = theta ),
        jnp . zeros_like ( x0 )
    ])

W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]])  # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ])  # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ])  # ODE parameters
X0 = fitz_init ( x0 , theta )  # initial value in rodeo format

# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.

# --- Define the prior process -------------------------------------------

n_vars = 2  # number of variables in the ODE
n_deriv = 3  # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars )  # IBM process scale factor


# --- data simulation ------------------------------------------------------

n_steps = 800  # number of evaluations steps
dt = ( t_max - t_min ) / n_steps  # step size

# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
    dt = dt_sim ,
    n_deriv = n_deriv ,
    sigma = sigma
)

# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )

Xt , _ = rodeo . solve_mv (
    key = key ,
    # define ode
    ode_fun = fitz_fun ,
    ode_weight = W ,
    ode_init = X0 ,
    t_min = t_min ,
    t_max = t_max ,
    theta = theta ,  # ODE parameters added here
    # solver parameters
    n_steps = n_steps ,
    interrogate = rodeo . interrogate . interrogate_kramer ,
    prior_weight = prior_Q ,
    prior_var = prior_R
)

نقارن الحل من الحل مع الحل الحتمي المقدم من odeint في مكتبة scipy .

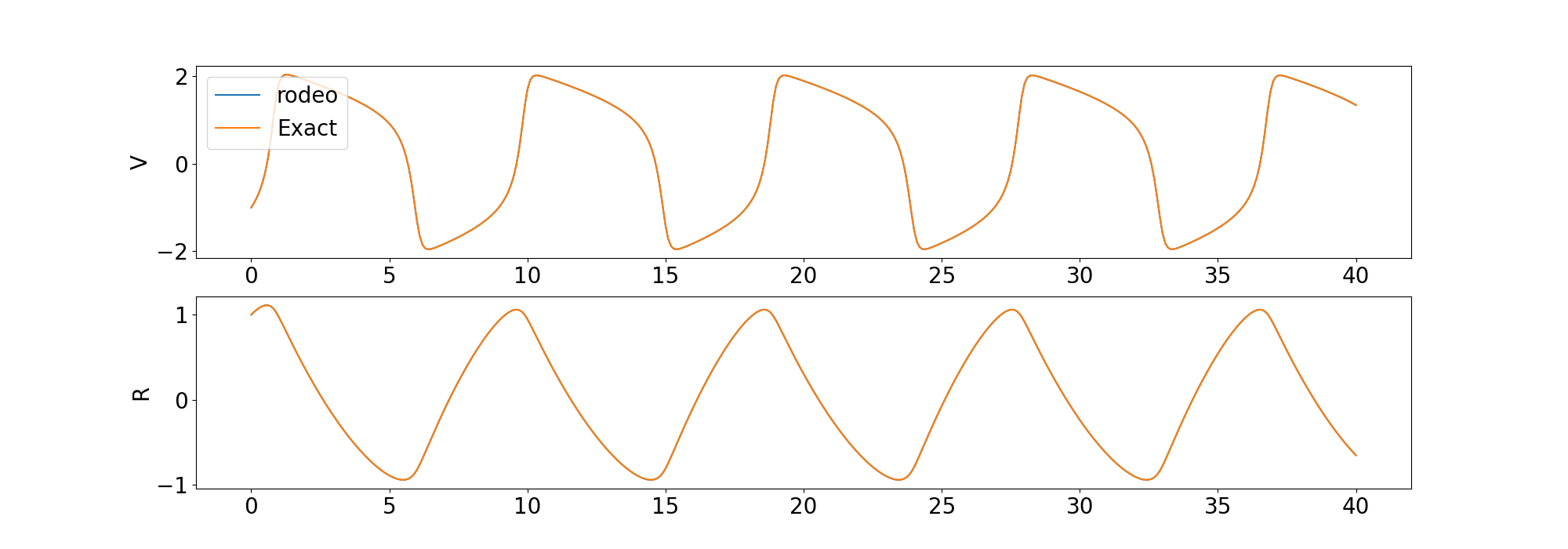
نقوم أيضًا بتضمين أمثلة لحل قصيدة ODE ذات الترتيب الأعلى وقصيدة ODE الفوضوية.

استنتاج المعلمة

ننتقل الآن إلى مشكلة استنتاج المعلمة. تحتوي مسابقات رعاة البقر على عدة طرق لتقريب الاحتمالات ملخصة في قسم الوصف. هنا، سوف نستخدم طريقة تقريب الاحتمالية basic . لنفترض أنه تم محاكاة الملاحظات عبر النموذج

$$ Y(t) sim textnormal{Normal}(X(t), phi^2 cdot boldsymbol{I}_{2times 2}) $$

أين $t=0, 1, ldots, 40$ و $فاي^2 = 0.005$ . المعلمات ذات الاهتمام هي $boldsymbol{Theta} = (أ، ب، ج، V(0)، R(0))$ مع $أ،ب،ج > 0$ . نحن نستخدم العادي السابق ل $(log a, log b, log c, V(0), R(0))$ مع يعني $0$ والانحراف المعياري 10 دولارات . يمكن استخدام الوظيفة التالية لإنشاء تقريب الاحتمال basic لـ $boldsymbol {ثيتا}$ .

 def fitz_logprior ( upars ):
    "Logprior on unconstrained model parameters."
    n_theta = 5  # number of ODE + IV parameters
    lpi = jax . scipy . stats . norm . logpdf (
        x = upars [: n_theta ],
        loc = 0. ,
        scale = 10.
    )
    return jnp . sum ( lpi )


def fitz_loglik ( obs_data , ode_data , ** params ):
    """
    Loglikelihood for measurement model.

    Args:
        obs_data (ndarray(n_obs, n_vars)): Observations data.
        ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
    """
    ll = jax . scipy . stats . norm . logpdf (
        x = obs_data ,
        loc = ode_data [:, :, 0 ],
        scale = 0.005
    )
    return jnp . sum ( ll )


def constrain_pars ( upars , dt ):
    """
    Convert unconstrained optimization parameters into rodeo inputs.

    Args:
        upars : Parameters vector on unconstrainted scale.
        dt : Discretization grid size.

    Returns:
        tuple with elements:
        - theta : ODE parameters.
        - X0 : Initial values in rodeo format.
        - Q, R : Prior matrices.
    """
    theta = jnp . exp ( upars [: 3 ])
    x0 = upars [ 3 : 5 ]
    X0 = fitz_init ( x0 , theta )
    sigma = upars [ 5 :]
    Q , R = rodeo . prior . ibm_init (
        dt = dt ,
        n_deriv = n_deriv ,
        sigma = sigma
    )
    return theta , X0 , Q , R


def neglogpost_basic ( upars ):
    "Negative logposterior for basic approximation."
    # solve ODE
    theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
    # basic loglikelihood
    ll = rodeo . inference . basic (
        key = key , 
        # ode specification
        ode_fun = fitz_fun ,
        ode_weight = W ,
        ode_init = X0 ,
        t_min = t_min ,
        t_max = t_max ,
        theta = theta ,
        # solver parameters
        n_steps = n_steps ,
        interrogate = rodeo . interrogate . interrogate_kramer ,
        prior_weight = prior_Q ,
        prior_var = prior_R ,
        # observations
        obs_data = obs_data ,
        obs_times = obs_times ,
        obs_loglik = fitz_loglik
    )
    return - ( ll + fitz_logprior ( upars ))

هذا مثال أساسي لتوضيح الاستخدام. نقترح تقديرات تقريبية أكثر تعقيدًا تعمل على نشر عدم اليقين في الحل إلى تقريب الاحتمالية مثل fenrir و marginal_mcmc و dalton . يرجى الرجوع إلى البرنامج التعليمي لاستدلال المعلمة لمزيد من التفاصيل.

نتائج

فيما يلي بعض النتائج الناتجة عن تقديرات الاحتمالية المختلفة الموجودة في مسابقات رعاة البقر من /examples/ :

فيتزهيو ناجومو

سيراه

هيس1

المطورين

اختبار الوحدة

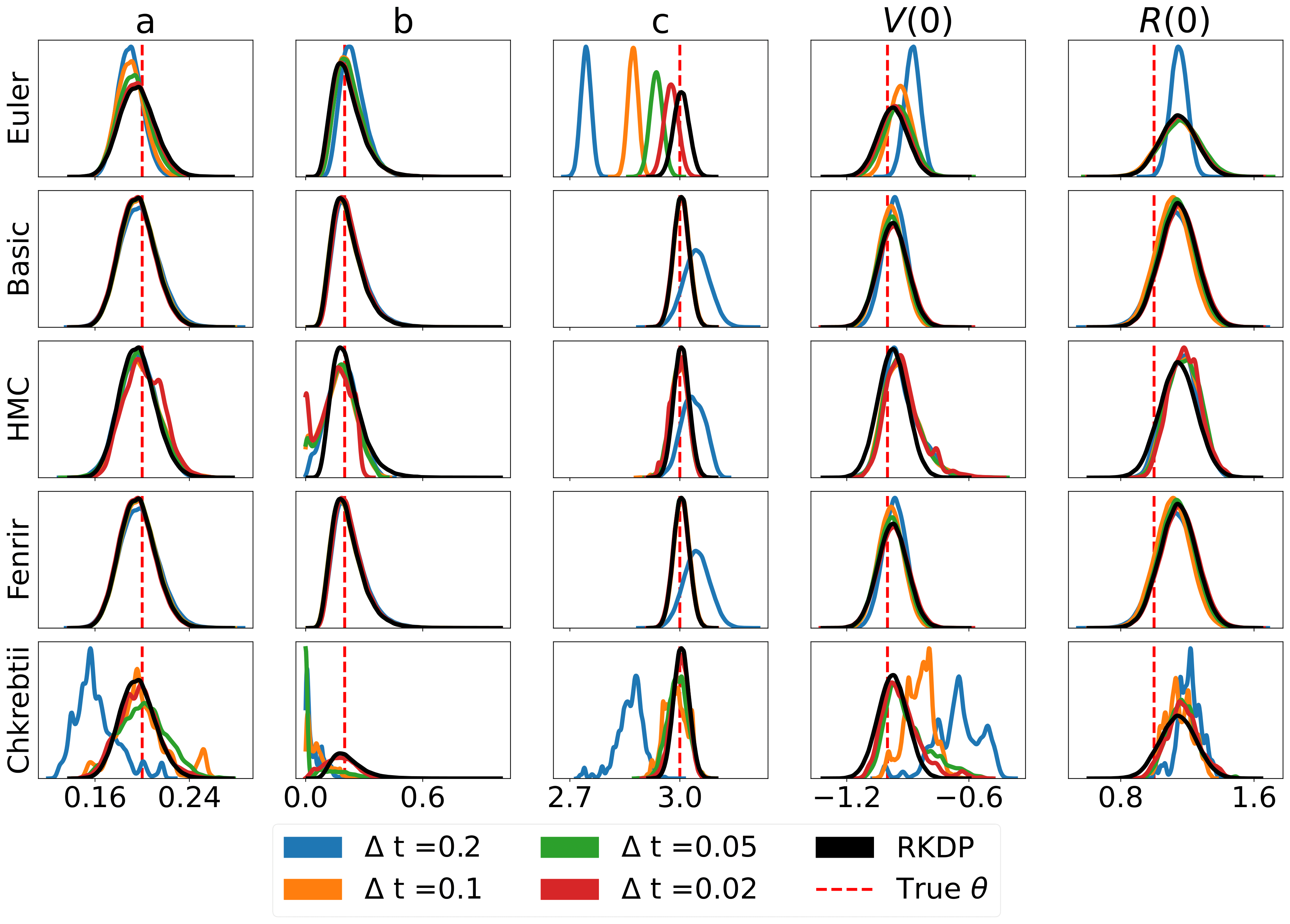
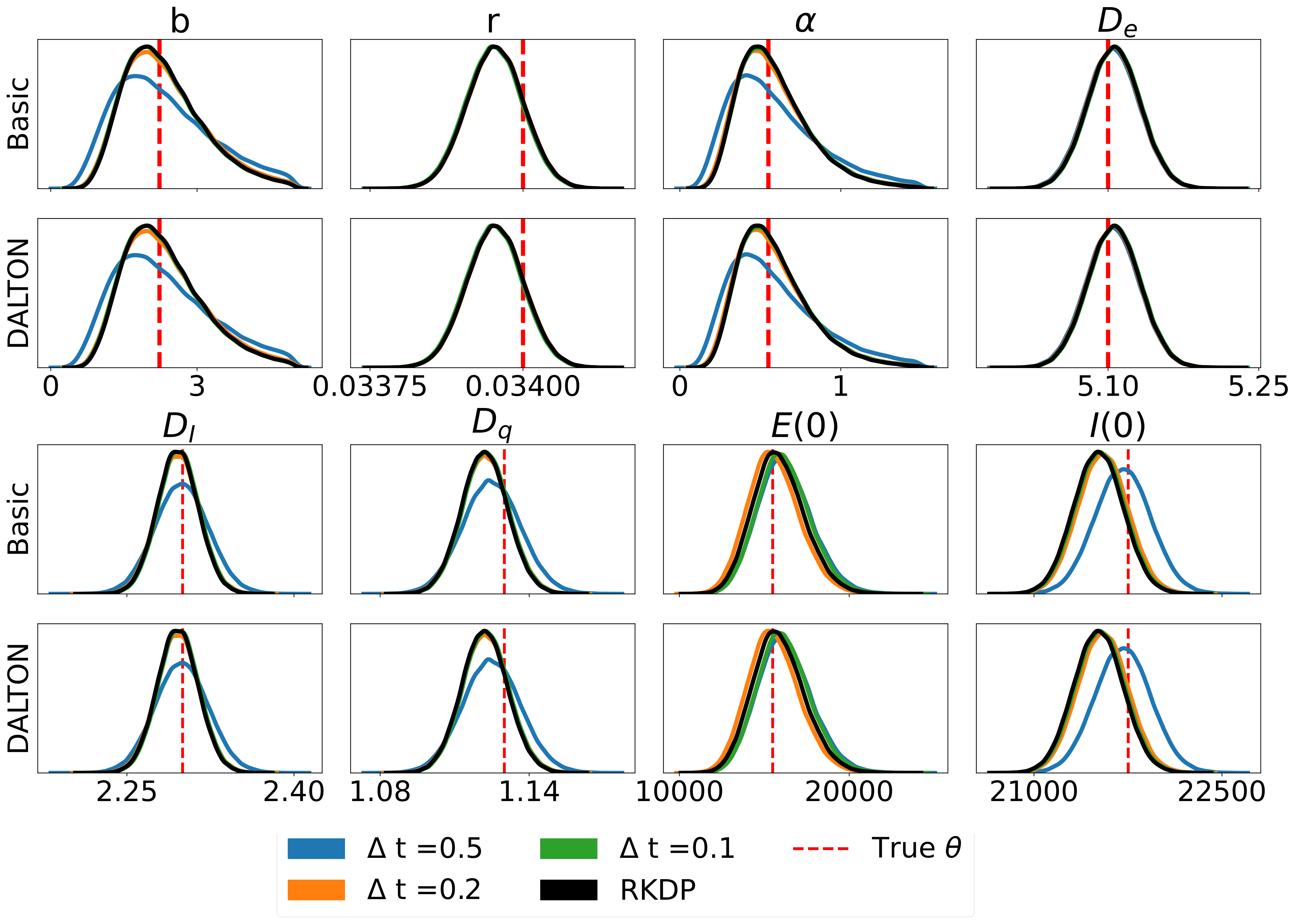
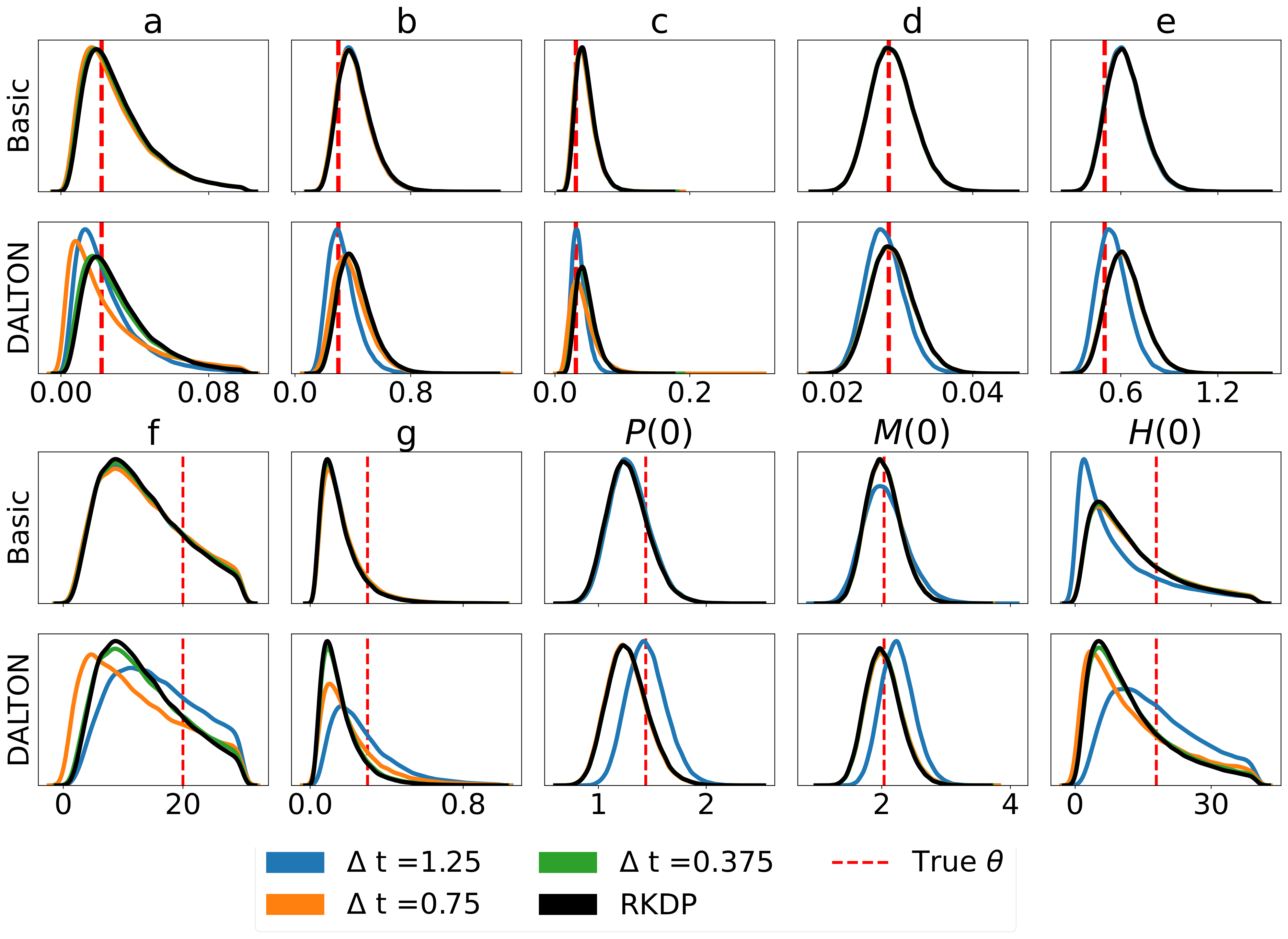
يمكن إجراء اختبارات الوحدة من خلال الأوامر التالية:

 cd tests
python -m unittest discover -v

أو قم بتثبيت tox ، ثم من داخل rodeo أدخل سطر الأوامر: tox .

توثيق البناء

يمكن تجميع وثائق HTML من المجلد الجذر:

pip install .[docs]
cd docs
make html

سيؤدي هذا إلى إنشاء الوثائق في docs/build .