يحل لغز برج هانوي عن طريق التعلم المعزز.
في بيئة Python مع تثبيت Numpy وPandas، قم بتشغيل البرنامج النصي hanoi.py لإنتاج المخططات الثلاثة الموضحة في قسم النتائج. يمكن بسهولة تعديل البرنامج النصي لتشغيل اللعبة باستخدام عدد مختلف من الأقراص N ، على سبيل المثال.
لقد حظي التعلم المعزز مؤخرًا باهتمام متجدد بعد التغلب على لاعب Go البشري المحترف بواسطة AlphaGo من Google Deepmind. هنا، تم حل لغز أبسط: لعبة برج هانوي. يتبع التنفيذ خوارزمية Q-learning كما اقترحها في الأصل Watkins & Dayan [1].
تتكون لعبة برج هانوي من ثلاثة أوتاد وعدد من الأقراص ذات الأحجام المختلفة التي يمكن أن تنزلق على الأوتاد. يبدأ اللغز بجميع الأقراص المكدسة على الوتد الأول بترتيب تصاعدي، بحيث يكون الأكبر في الأسفل والأصغر في الأعلى. الهدف من اللعبة هو نقل جميع الأقراص إلى الوتد الثالث. التحركات القانونية الوحيدة هي تلك التي تأخذ القرص العلوي من ربط إلى آخر، مع تقييد عدم وضع قرص على قرص أصغر. يوضح الشكل 1 الحل الأمثل لأربعة أقراص.

الشكل 1. حل متحرك للغز برج هانوي مكون من 4 أقراص. (المصدر: ويكيبيديا).
باتباع أندرسون [2]، قمنا بتمثيل حالة اللعبة من خلال الصفوف، حيث يشير العنصر i إلى الرابط الذي تم تشغيل القرص i به. يتم تسمية الأقراص حسب الحجم المتزايد. وبالتالي، فإن الحالة الأولية هي (111)، والحالة النهائية المطلوبة هي (333) (الشكل 2).
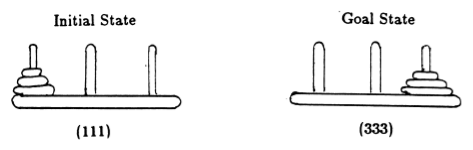
الشكل 2. الحالات الأولية والهدف من لغز برج هانوي المكون من 3 أقراص. (من [2]).
تشكل حالات اللغز والانتقالات بينها المقابلة للحركات القانونية الرسم البياني لانتقال حالة اللغز، والذي يظهر في الشكل 3.
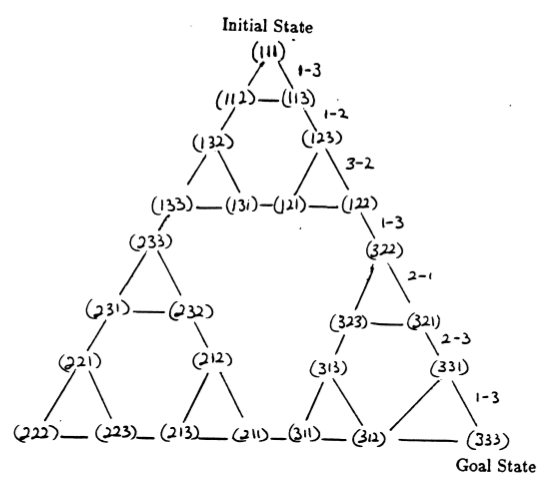
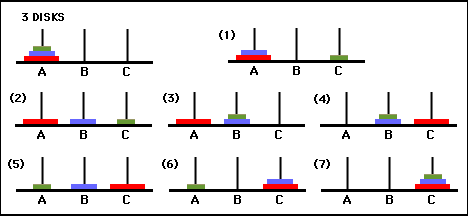
الشكل 3. الرسم البياني الانتقالي لحالة لغز برج هانوي المكون من ثلاثة أقراص (أعلاه) والحل الأمثل المقابل للحركة السبعة (أدناه)، والذي يتبع مسار الجانب الأيمن من الرسم البياني. (من [2] و Mathforum.org).
الحد الأدنى لعدد الحركات المطلوبة لحل لغز برج هانوي هو 2 N - 1، حيث N هو عدد الأقراص. وبالتالي بالنسبة لـ N = 3، يمكن حل اللغز في 7 حركات، كما هو موضح في الشكل 3. وفي القسم التالي، نوضح كيفية تحقيق ذلك من خلال Q-learning.
R ومصفوفة "قيمة الإجراء" Q لقرصين الخطوة الأولى في البرنامج هي إنشاء مصفوفة المكافآت R التي تلتقط قواعد اللعبة وتمنح مكافأة للفوز بها. للتبسيط، يتم عرض مصفوفة المكافأة للأقراص N = 2 في الشكل 4.
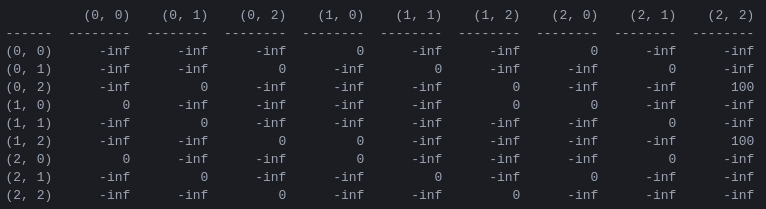
الشكل 4. مصفوفة المكافأة R للغز برج هانوي مع N = 2 قرص. يمثل العنصر ( i , j ) مكافأة الانتقال من الحالة i إلى j . يتم تصنيف الحالات بواسطة صفوف كما في الشكلين 2 و3، مع اختلاف أن الأوتاد مفهرسة "بشكل بايثوني" من 0 إلى 2 بدلاً من 1 إلى 3. يتم تعيين مكافأة للتحركات التي تؤدي إلى حالة الهدف (2،2). من 100، التحركات غير القانونية من، وجميع التحركات الأخرى من 0.
تصف مصفوفة المكافآت R المكافآت الفورية فقط: لا يمكن تحقيق مكافأة قدرها 100 إلا من الحالات قبل الأخيرة (0،2) و (1،2). في الحالات الأخرى، كل من النقلتين أو الثلاث الممكنات لها مكافأة متساوية قدرها 0، ولا يوجد سبب واضح لاختيار واحدة على الأخرى.
في النهاية، نسعى إلى تعيين "قيمة" لكل حركة محتملة في كل حالة، بحيث يمكننا من خلال تعظيم هذه القيم تحديد سياسة تؤدي إلى الحل الأمثل. تسمى مصفوفة "القيم" لكل إجراء في كل حالة Q ويمكن حلها بشكل متكرر أو "تعلمها" بطريقة عشوائية كما وصفها واتكينز وديان [1]. وتظهر النتيجة لقرصين في الشكل 5.
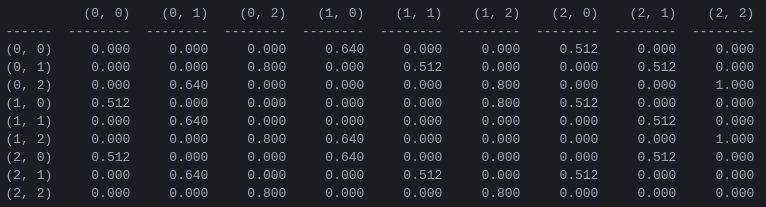
الشكل 5. مصفوفة "قيمة العمل" Q للعبة برج هانوي التي تحتوي على قرصين، تم تعلمها باستخدام عامل خصم = 0.8، وعامل التعلم = 1.0، و1000 حلقة تدريبية.
قيم المصفوفة Q هي في الأساس أوزان يمكن تخصيصها لرؤوس الرسم البياني لانتقال الحالة في الشكل 3، والتي توجه العامل من الحالة الأولية إلى الحالة المستهدفة بأقصر طريقة ممكنة. في هذا المثال، من خلال البدء بالحالة (0,0) واختيار الحركة ذات القيمة الأعلى لـ Q بشكل متتابع، يمكن للقارئ إقناع نفسه بأن مصفوفة Q تقود الوكيل عبر تسلسل الحالات (0,0) - (1) ,0) - (1,2) - (2,2)، وهو ما يتوافق مع الحل الأمثل المكون من 3 حركات للعبة Tower of Hanoi ذات القرصين (الشكل 6).
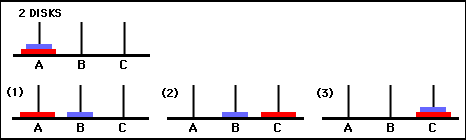
الشكل 6. حل لعبة برج هانوي بقرصين. يتم تمثيل الحالات المتتالية بـ (0,0)، (1،0)، (1،2)، و (2،2) على التوالي. (المصدر: mathforum.org).
في هذا المثال حيث تقاربت المصفوفة Q إلى قيمتها المثلى، فإنها تحدد سياسة ثابتة : يحتوي كل صف على إجراء واحد بقيمة قصوى فريدة. ومع ذلك، أثناء عملية التعلم، قد يكون للإجراءات المختلفة نفس قيمة Q . (على وجه الخصوص، هذا هو الحال في بداية التدريب عندما تتم تهيئة Q إلى مصفوفة من الأصفار). في عمليات المحاكاة المقدمة في القسم التالي، يتم التعامل مع مثل هذه المواقف من خلال السياسة العشوائية التالية: في الحالات التي يتم فيها تقاسم الحد الأقصى لقيمة Q بين عدة إجراءات، اختر أحد هذه الإجراءات بشكل عشوائي.
يمكن قياس أداء خوارزمية التعلم Q من خلال حساب عدد الحركات التي تستغرقها (في المتوسط) لحل لغز برج هانوي. ويتناقص هذا العدد مع عدد حلقات التدريب حتى يصل في النهاية إلى القيمة المثلى 2 N - 1، حيث N هو عدد الأقراص، كما هو موضح في الشكل 7 لـ N = 2 و3 و4.
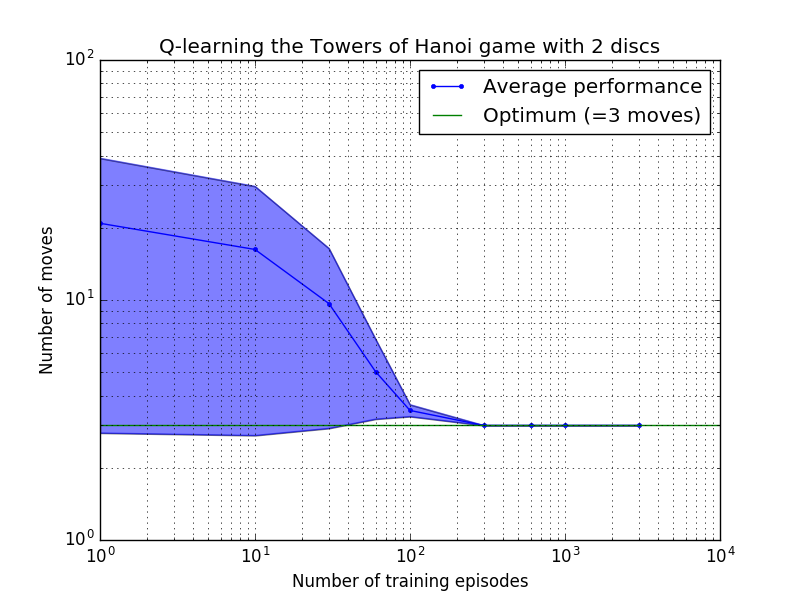
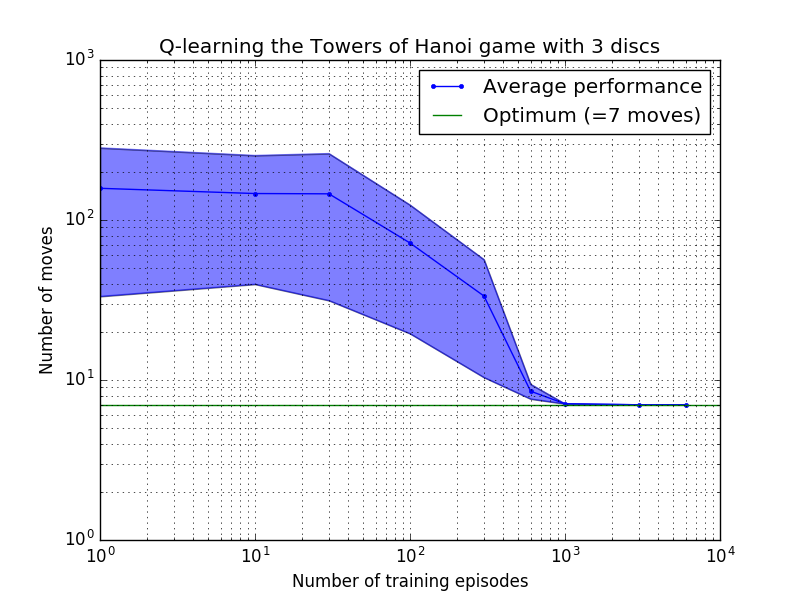
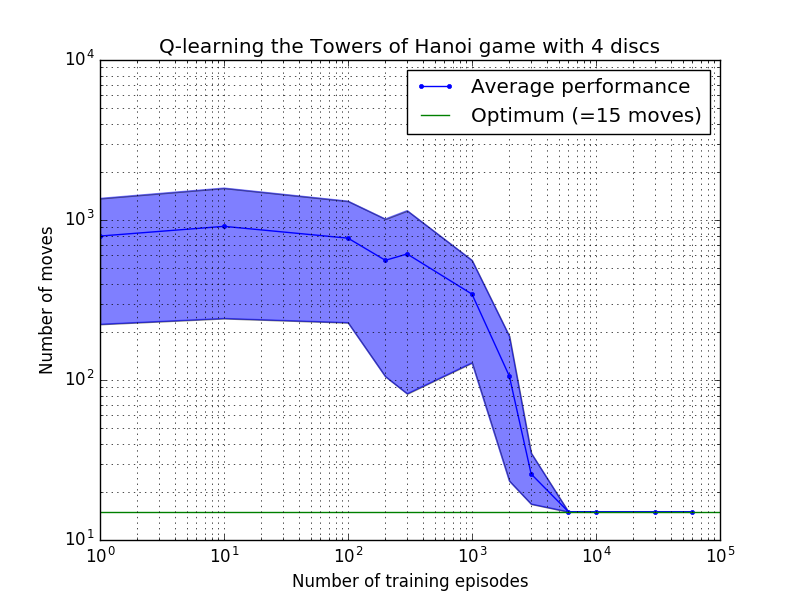
الشكل 7. أداء خوارزمية Q-learning للعبة برج هانوي باستخدام 2 و3 و4 أقراص من الأعلى إلى الأسفل. في جميع الحالات تم إجراء التعلم بعامل خصم = 0.8 وعامل تعلم = 1.0. يمثل المنحنى الأزرق الثابت متوسط الأداء خلال 100 فترة من التدريب ولعب اللعبة 100 مرة لكل سياسة عشوائية ناتجة. يتم تعويض الحدود العلوية والسفلية للمنطقة المظللة باللون الأزرق عن المتوسط بواسطة الانحراف المعياري المقدر. (بالنسبة لـ N = 3 و N = 4، تم تخفيض عدد حلقات التدريب وأوقات اللعب إلى 10 و10، على التوالي، بسبب القيود الحسابية).
من السمات المثيرة للاهتمام لخصائص التعلم في الشكل 7 أنه في جميع الحالات، يكون التعلم بطيئًا في البداية، ولا يكاد يكون أداء الوكيل أفضل من سياسة "التدريب الصفري" المتمثلة في اختيار الحركات بشكل عشوائي. في مرحلة ما يصل التعلم إلى "نقطة انعطاف" ثم يتقارب إلى العدد الأمثل من التحركات بوتيرة متسارعة (على الرغم من أن هذا مبالغ فيه إلى حد ما بالمقياس اللوغاريتمي).
نجح برنامج Python في حل لغز برج هانوي على النحو الأمثل لأي عدد من الأقراص من خلال Q-learning. يمكن تكييف البرنامج النصي بسهولة مع المشكلات الأخرى باستخدام مصفوفة مكافآت مختلفة R .
عدد حلقات التدريب المطلوبة للتوصل إلى الحل الأمثل يزداد بشكل كبير مع عدد الأقراص N : بالنسبة لعدد N=2 من الأقراص، يستغرق الأمر حوالي 300 حلقة، بينما بالنسبة لـ N=4 يستغرق الأمر حوالي 6000. قد يكون التحسين المحتمل لخوارزمية التعلم هو السماح لها بالبحث تلقائيًا عن الحلول العودية، كما فعل هينجست [3].
[ 1 ] واتكينز وديان، التعلم Q ، التعلم الآلي، 8، 279-292 (1992). (بي دي إف).
[ 2 ] أندرسون، التعلم وحل المشكلات باستخدام أنظمة الاتصال متعددة الطبقات ، دكتوراه. أطروحة (1986). (بي دي إف).
[ 3 ] هنغست، اكتشاف التسلسل الهرمي في التعلم المعزز باستخدام HEXQ ، وقائع المؤتمر الدولي التاسع عشر للتعلم الآلي (2002). (بي دي إف).