تطبيق خوارزمية Minimax AI على لعبة Tic-Tac-Toe (أو Noughts and Crosses). جربه: تيك تاك تو - مينيماكس
لحل الألعاب باستخدام الذكاء الاصطناعي، سنقدم مفهوم شجرة الألعاب متبوعة بخوارزمية minimax. يتم تمثيل الحالات المختلفة للعبة بواسطة عقد في شجرة اللعبة، وهي تشبه إلى حد كبير مشاكل التخطيط المذكورة أعلاه. الفكرة مختلفة قليلاً. في شجرة اللعبة، يتم ترتيب العقد في مستويات تتوافق مع أدوار كل لاعب في اللعبة بحيث تكون العقدة "الجذر" للشجرة (الموضحة عادةً في الجزء العلوي من الرسم التخطيطي) هي موضع البداية في اللعبة. في لعبة tic-tac-toe، ستكون هذه هي الشبكة الفارغة التي لم يتم تشغيل X أو Os حتى الآن. تحت الجذر، في المستوى الثاني، هناك الحالات المحتملة التي يمكن أن تنتج عن تحركات اللاعب الأول، سواء كانت X أو O. ونحن نسمي هذه العقد "أبناء" العقدة الجذرية.
كل عقدة في المستوى الثاني سيكون لها أيضًا نقاط فرعية للحالات التي يمكن الوصول إليها منها من خلال تحركات اللاعب المنافس. ويستمر هذا، مستوى تلو الآخر، حتى الوصول إلى الحالات التي تنتهي فيها اللعبة. في لعبة تيك تاك تو، يعني هذا أن أحد اللاعبين يحصل على خط من ثلاثة ويفوز، أو أن اللوحة ممتلئة وتنتهي اللعبة بالتعادل.
Minimax هو ذكاء اصطناعي يتم تطبيقه في ألعاب ثنائية اللاعبين، مثل لعبة tic-tac-toe ولعبة الداما والشطرنج ولعبة Go. تُعرف هذه الألعاب باسم الألعاب ذات المحصلة الصفرية، لأنه في التمثيل الرياضي: يفوز أحد اللاعبين (+1) ويخسر اللاعب الآخر (-1) أو لا يفوز كليهما (0).
تبحث الخوارزمية، بشكل متكرر، عن أفضل حركة تؤدي إلى فوز اللاعب Max أو عدم خسارته (التعادل). إنه يأخذ في الاعتبار الحالة الحالية للعبة والتحركات المتاحة في تلك الحالة، ثم يلعب لكل حركة صالحة (بالتناوب بين الحد الأدنى والحد الأقصى ) حتى يجد الحالة النهائية (الفوز أو التعادل أو الخسارة).
تمت دراسة الخوارزمية من خلال كتاب الخوارزميات باختصار (جورج هاينمان؛ غاري بوليس؛ ستانلي سيلكو، 2009). الكود الزائف (مقتبس):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
سنرى الآن كل جزء من هذا الكود الزائف مع تطبيق بايثون. تطبيق Python متاح في هذا المستودع. بادئ ذي بدء، فكر في الأمر:
اللوحة = [ [0، 0، 0]، [0، 0، 0]، [0، 0، 0] ]
الحد الأقصى = +1
الحد الأدنى = -1
الحد الأقصى قد يكون X أو O وقد يكون الحد الأدنى O أو X، أيًا كان. اللوحة 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]يبدأ كلا اللاعبين بأسوأ درجاتك. إذا كان اللاعب هو MAX، فإن نتيجته هي -infinity. وإلا، إذا كان اللاعب هو الحد الأدنى، فإن نتيجته هي +اللانهاية. ملحوظة: infinity هو اسم مستعار لـ inf (من وحدة الرياضيات في Python).
أفضل حركة على اللوحة هي [-1، -1] (الصف والعمود) للجميع.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreإذا كان العمق يساوي صفرًا، فهذا يعني أن اللوحة لا تحتوي على خلايا فارغة جديدة للعب. أو، إذا فاز أحد اللاعبين، فستنتهي اللعبة بحد أقصى أو أدنى. لذلك سيتم إرجاع النتيجة لتلك الحالة.
سنرى الآن الجزء الرئيسي من هذا الكود الذي يحتوي على العودية.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yلكل تحركات صالحة (خلايا فارغة):
يتم التراجع عن الحركة (+1 أو -1) على اللوحة ويتم جمع الصف والعمود.
والخطوة التالية هي مقارنة النتيجة مع الأفضل.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreبالنسبة للاعب MAX، سيتم الحصول على درجة أكبر. بالنسبة للاعب MIN، سيتم الحصول على درجة أقل. وفي النهاية، يتم إرجاع أفضل خطوة. الخوارزمية النهائية:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best أدناه، أفضل حركة هي في المنتصف لأن القيمة القصوى موجودة في العقدة الثانية على اليسار.
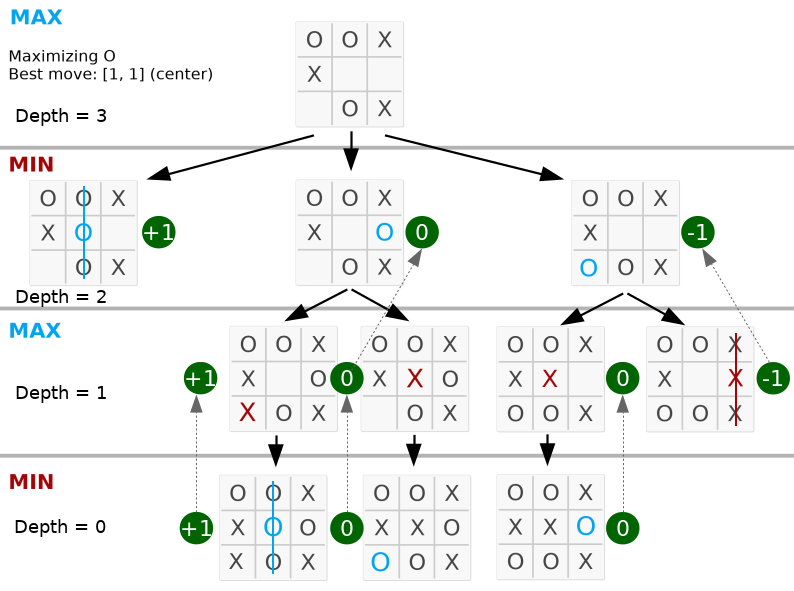
ألقِ نظرة على أن العمق يساوي التحركات الصحيحة على اللوحة. الكود الكامل متاح في py_version/ .
شجرة اللعبة المبسطة:
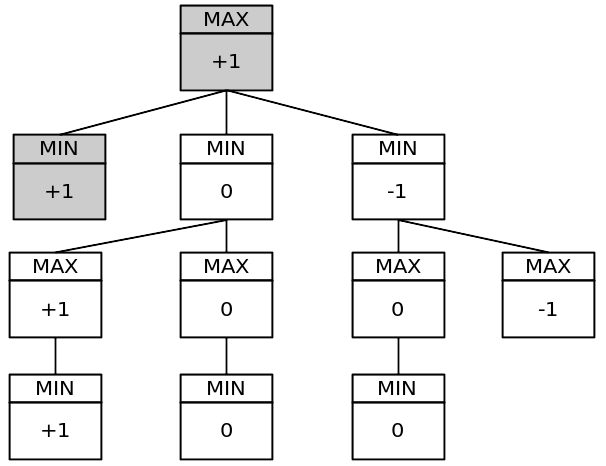
تحتوي هذه الشجرة على 11 عقدة. تحتوي شجرة اللعبة الكاملة على 549.946 عقدة! يمكنك اختباره من خلال وضع متغير عام ثابت في برنامجك وزيادته لكل استدعاء دالة minimax لكل دورة.
في لعبة أكثر تعقيدًا، مثل الشطرنج، من الصعب البحث في شجرة اللعبة بأكملها. ومع ذلك، فإن Alpha–beta Pruning هو أسلوب تحسين لخوارزمية minimax التي تسمح لنا بتجاهل بعض الفروع في شجرة البحث، لأنه يقطع العقد (الأشجار الفرعية) غير ذات الصلة في البحث. لمزيد من المعلومات، انظر: