
مقدم الفريق: Kahraman Kostas
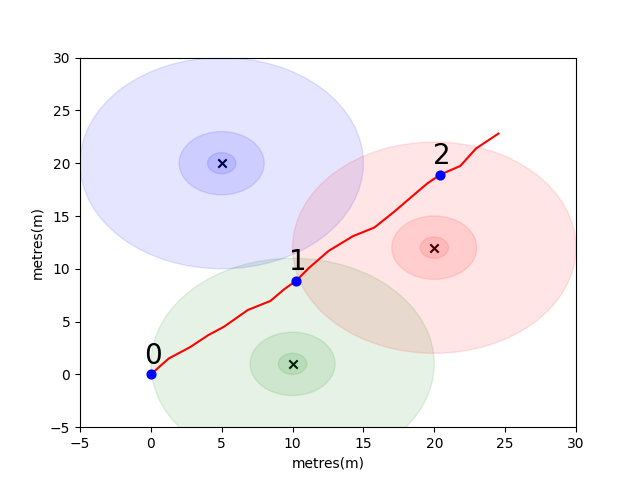
لتبدأ ، قمنا بتجميع مشكلة بسيطة لتقديم بعض مفاهيم المواقع الداخلية الرئيسية. ضع في اعتبارك البيئة التالية: يسافر المستخدم في مساحة مفتوحة في وجود 3 بواعث WiFi (نسمي البيانات التي أنشأها هذا المستخدم مسارًا). كل باعتر لديه عنوان MAC فريد. تم تجهيز المستخدم بهاتف ذكي يقوم بمسح بيئة WiFi بشكل دوري وتسجيل RSSI لكل MAC المكتشف (في DB).
بالنسبة لهذا النموذج ، استخدمنا نموذجًا قياسيًا لانتشار الفضاء الحرة لخسارة السجل لكل من البوابات. هذا نموذج مبسط يعمل بشكل جيد في الفضاء الحر ، لكنه ينهار في بيئات داخلية حقيقية مع الجدران والعقبات الأخرى التي يمكن أن ترتد الإشارات حولها بطريقة أكثر تعقيدًا. بشكل عام ، نتوقع أن نرى انخفاضًا حادًا في RSSI على مسافة حيث تنتشر الطاقة الثابتة من الهوائي المنبعث على مساحة متزايدة مع انتشار الموجة. في الرسم البياني أسفل كل دائرة تشير إلى انخفاض 10dB.
يسير المستخدم شمال شرق من بوينت (0،0) وهناك يجري ثلاثة عمليات مسح للبيئة. ويرد أدناه البيانات المسجلة في كل فحص.
scan 0 -> {'green': -60, 'blue': -66, 'red': -67}
scan 1 -> {'green': -58, 'blue': -61, 'red': -60}
scan 2 -> {'green': -66, 'blue': -62, 'red': -59}
الخصائص المعقدة والفريدة المحلية لبيئة WiFi تجعلها مفيدة للغاية لأنظمة تحديد المواقع الداخلية. على سبيل المثال ، في scan 1 تقريبًا في النقطه الوسطى للباعبين الثلاثة ولا يوجد مكان آخر في هذه البيئة حيث يمكن للمرء أن يأخذ قراءة من شأنها تسجيل قيم RSSI مماثلة. بالنظر إلى مجموعة من عمليات المسح أو "بصمات الأصابع" من المسارات المستقلة ، نحن مهتمون بحساب مدى تشابهها في مساحة WiFi لأن هذا مؤشر على مدى قربهم في الفضاء الحقيقي.
التحدي الأول هو كتابة وظيفة لحساب مسافة الإقليدية ومقاييس مسافة مانهاتن بين كل من عمليات المسح في مسار العينة التي قدمناها أعلاه. يعد استخدام البيانات من مسار واحد وسيلة جيدة لاختبار جودة مقياس التشابه حيث يمكننا الحصول على تقديرات دقيقة إلى حد ما للمسافة الحقيقية باستخدام البيانات من وحدة القياس بين الهاتف (IMU) التي تستخدمها أحد المشاة الميت. (PDR) الوحدة النمطية.
def euclidean ( fp1 , fp2 ):
raise NotImplementedError
def manhattan ( fp1 , fp2 ):
raise NotImplementedError # solution of the above functions
from scipy . spatial import distance
def euclidean ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . euclidean ( fp1 , fp2 )
def manhattan ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . cityblock ( fp1 , fp2 ) import json
import numpy as np
import matplotlib . pyplot as plt
from metrics import eval_dist_metric
with open ( "intro_trajectory_1.json" ) as f :
traj = json . load ( f )
## Pre-calculate the pair indexes we are interested in
keys = []
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
# only calculate the upper triangle
if fp1 [ 'step_index' ] > fp2 [ 'step_index' ]:
keys . append (( fp1 [ 'step_index' ], fp2 [ 'step_index' ]))
## Get the distances from PDR
true_d = {}
for step1 in traj [ 'steps' ]:
for step2 in traj [ 'steps' ]:
key = ( step1 [ 'step_index' ], step2 [ 'step_index' ])
if key in keys :
true_d [ key ] = abs ( step1 [ 'di' ] - step2 [ 'di' ])
euc_d = {}
man_d = {}
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
key = ( fp1 [ 'step_index' ], fp2 [ 'step_index' ])
if key in keys :
euc_d [ key ] = euclidean ( fp1 [ 'profile' ], fp2 [ 'profile' ])
man_d [ key ] = manhattan ( fp1 [ 'profile' ], fp2 [ 'profile' ])
print ( "Euclidean Average Error" )
print ( f' { eval_dist_metric ( euc_d , true_d ):.2f } ' )
print ( "Manhattan Average Error" )
print ( f' { eval_dist_metric ( man_d , true_d ):.2f } ' ) Euclidean Average Error
9.29
Manhattan Average Error
4.90
إذا قمت بتطبيق الوظائف بشكل صحيح ، فيجب أن ترى أن متوسط الخطأ في مقياس الإقليدي كان 9.29 بينما كان مانهاتن هو 4.90 فقط. لذلك بالنسبة لهذه البيانات ، فإن مسافة مانهاتن هي تقدير أفضل للمسافة الحقيقية.
هذا بالطبع نموذج مبسط للغاية. في الواقع ، لا توجد علاقة مباشرة بين قيم RSSI ومسافة الفضاء الحرة بهذه الطريقة. عادة ، عندما ننشئ تقديراتنا الخاصة للمسافة ، سنستخدم مسافات PDR المعروفة من داخل مسار لتناسب النتيجة الرقمية مع تقدير المسافة المادية.
لتحديك الرئيسي ، نود منك تطوير مقياسك الخاص لتقدير المسافة الواقعية بين فحوصات ، استنادًا إلى بصمات واي فاي فقط. سنوفر لك بيانات حقيقية تم جمعها في وقت مبكر من عام 2021 من مركز تجاري واحد. ستحتوي البيانات على 114661 بصمات الأصابع و 879824 مسافة بين عمليات الفحص. ستكون المسافات هي أفضل تقدير لدينا للمسافة الحقيقية بالنظر إلى معلومات إضافية سنأخذها في الاعتبار.
سنقدم مجموعة اختبار من أزواج بصمات الأصابع وستحتاج إلى كتابة وظيفة تخبرنا إلى أي مدى تبعدها.
يمكن أن تكون هذه الوظيفة بسيطة مثل التباين في أحد المقاييس التي قدمناها أعلاه أو معقدة مثل حل التعلم الآلي الكامل الذي يتعلم وزن عناوين MAC مختلفة (أو مجموعات عناوين MAC) بشكل مختلف في مواقف مختلفة.
بعض النقاط النهائية للنظر:
يتم تجميع البيانات على أنها ثلاثة ملفات لك.
يحتوي task1_fingerprints.json على جميع معلومات البصمات للمشكلة. هذا هو كل إدخال يمثل فحصًا حقيقيًا لبعثات WiFi في منطقة المركز التجاري. ستجد أن نفس عناوين MAC ستكون موجودة في العديد من بصمات الأصابع.
يحتوي task1_train.csv على أزواج التدريب الصحيحة لمساعدتك في تصميم/تدريب الخوارزمية الخاصة بك. يحتوي كل زوج id1-id2 على مسافة الحقيقة المسمى (بالأمتار) ويتوافق كل معرف مع بصمات الأصابع من task1_fingerprints.json .
task1_test.csv هو نفس تنسيق task1_train.csv ولكنه لا يحتوي على عمليات النزوح. هذه هي ما نود أن تتنبأ به باستخدام معلومات البصمة الخام.
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
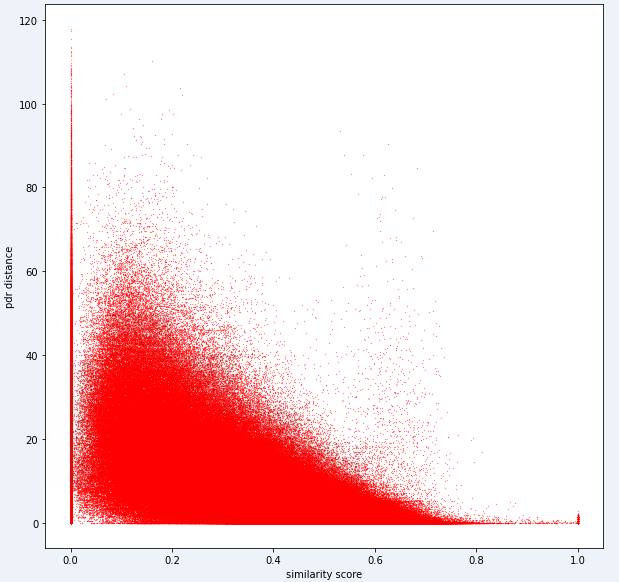
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]])في نهاية المطاف ، يجب أن يكون النموذج المثالي قادرًا على العثور على رسم خرائط دقيق بين مساحة بصمة البصمة ذات الأبعاد العالية (يمكن أن تحتوي بصمة واحدة على العديد من القياسات) ومسافة المسافة الأبعاد الأولى. قد يكون من المفيد رسم مسافة PDR (من بيانات التدريب) مقابل بعض مقياس التشابه المحسوب لمعرفة ما إذا كان المقياس يكشف عن اتجاه واضح. يجب أن يرتبط التشابه العالي بمسافة منخفضة.
فيما يلي مقياس مسافة واحد نستخدمه داخليًا لهذه المهمة. يمكنك أن ترى أنه حتى بالنسبة لهذا المقياس ، لدينا قدر كبير من الضوضاء.
بسبب هذا المستوى من الضوضاء ، سيكون مقياس التسجيل الخاص بنا للمهمة 1 متحيزًا نحو الدقة على الاستدعاء
يجب أن يستخدم التقديم الخاص بك المعرفات الدقيقة من ملف test1_test.csv ويجب أن يملأ عمود الإزاحة الثالث (الفارغ حاليًا) مع المسافة المقدرة (بالأمتار) لزوج البصمات.
def my_distance_function ( fp1 , fp2 ):
raise NotImplementedError output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
fp1 = fps [ id1 ]
fp2 = fps [ id2 ]
distance_estimate = my_distance_function ( fp1 , fp2 )
output_data . append ([ id1 , id2 , distance_estimate ])
with open ( "MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )يمكن تلخيص الخطوات في المهمة الأولى على النحو التالي.
تم توضيح هذه الخطوات في الصورة أدناه.

استخدمنا Python 3.6.5 لإنشاء ملف التطبيق. قمنا بتضمين بعض الوحدات الإضافية التي لم يتم تضمينها في ملف المثال المقدم في بداية المنافسة. يمكن إدراج هذه الوحدات النمطية على النحو التالي:
| الأذواق | مهمة |
|---|---|
| Tensorflow | التعلم العميق |
| الباندا | تحليل البيانات |
| سكيبي | الحوسبة المسافة |
بدأنا بتركيب هذه الوحدات كخطوة أولى.
## 1.1 Installing modules
!p ip install tensorflow == 2.6 . 2
!p ip install scipy
!p ip install pandas في هذه الخطوة ، قمنا بإصلاح البذور العشوائية ذات الصلة لاستخدامها من أجل الحصول على نتائج قابلة للتكرار. وبهذه الطريقة ، قدمنا مسارًا حتميًا حيث نحصل على نفس النتيجة في كل تشغيل. ومع ذلك ، وفقًا لملاحظاتنا ، قد تختلف النتائج التي تم الحصول عليها باستخدام أجهزة كمبيوتر مختلفة قليلاً (± 1 ٪)
## 1.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )
import tensorflow as tf
tf . random . set_seed ( seed_value )
import tensorflow as tf
session_conf = tf . compat . v1 . ConfigProto ( intra_op_parallelism_threads = 1 , inter_op_parallelism_threads = 1 )
sess = tf . compat . v1 . Session ( graph = tf . compat . v1 . get_default_graph (), config = session_conf ) في هذا القسم ، نقوم بتحميل البيانات التي سنستخدمها. أخذنا الرمز والتفسيرات من ملف العينة المعطى ( Task1-IPS-Challenge-2021.ipynb ).
يحتوي task1_fingerprints.json على جميع معلومات البصمات للمشكلة. هذا هو كل إدخال يمثل فحصًا حقيقيًا لبعثات WiFi في منطقة المركز التجاري. ستجد أن نفس عناوين MAC ستكون موجودة في العديد من بصمات الأصابع.
يحتوي task1_train.csv على أزواج التدريب الصحيحة لمساعدتك في تصميم/تدريب الخوارزمية الخاصة بك. يحتوي كل زوج id1-id2 على مسافة الحقيقة المسمى (بالأمتار) ويتوافق كل معرف مع بصمات الأصابع من task1_fingerprints.json .
task1_test.csv هو نفس تنسيق task1_train.csv ولكنه لا يحتوي على عمليات النزوح.
## 1.3 Loading the data
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]]) 879824it [05:16, 2778.31it/s]
5160445it [01:00, 85269.27it/s]
في هذه الخطوة ، نقوم بإجراء استخراج الميزات باستخدام وظيفتين. feature_extraction_file ، تقوم ببساطة بسحب القيم ذات الصلة لبصمات الأصابع (في الأزواج) من ملف JSON ويرسلها إلى دالة feature_extraction لإجراء الحسابات.
في وظيفة feature_extraction ، إذا كان هذان بصمات الأصابع يختلفان عن بعضهما البعض من حيث الحجم والأجهزة التي تحتوي عليها ، يتم جمع جميع الأجهزة المدرجة في بصمات الأصابع لتشكيل تسلسل شائع دون التكرار. في كل صفيف ، نجعل هاتين المصفوفتين متطابقة (من حيث الأجهزة التي تتضمنها) عن طريق تعيين القيمة 0 للأجهزة غير المقابلة. يتم شرح هذه العملية مع مثال في الصورة التالية.
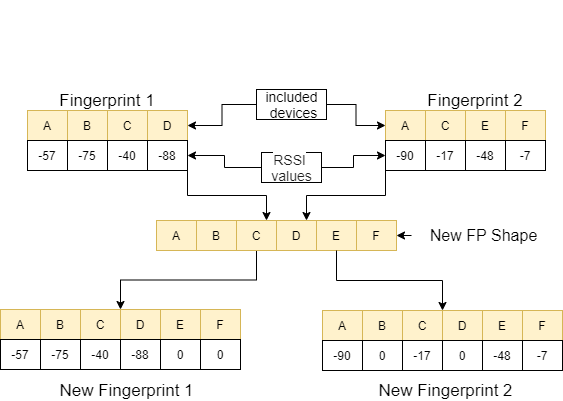
يتم حساب المسافة بين هاتين بصمات الأصابع ، والتي يتم تصنيعها ، باستخدام 11 طريقة مختلفة [1]. هذه الطرق هي:
بعد ذلك ، يتم توجيه هذه القيم إلى وظيفة feature_extraction_file وحفظها كملف CSV ضمن هذه الوظيفة. بمعنى آخر ، تتحول بصمات الأصابع بأحجام مختلفة إلى ملف CSV 11 ميزة نتيجة لهذه العملية. يتم تدريب النموذج المراد استخدامه واختباره باستخدام هذه الميزات التي تم إنشاؤها حديثًا.
## 1.4 Feature Extraction
def feature_extraction_file ( data , name , flag ):
features = [[ "braycurtis" ,
"canberra" ,
"chebyshev" ,
"cityblock" ,
"correlation" ,
"cosine" ,
"euclidean" ,
"jensenshannon" ,
"minkowski" ,
"sqeuclidean" ,
"wminkowski" , "real" ]]
for i in tqdm (( data ), position = 0 , leave = True ):
fp1 = fps [ i [ 0 ]]
fp2 = fps [ i [ 1 ]]
feature = feature_extraction ( fp1 , fp2 )
if flag :
feature . append ( i [ 2 ])
else : feature . append ( 0 )
features . append ( feature )
with open ( name , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( features )
#print(features) ## 1.4 Feature Extraction
def feature_extraction ( fp1 , fp2 ):
mac = set ( list ( fp1 . keys ()) + list ( fp2 . keys ()))
mac = { i : 0 for i in mac }
f1 = mac . copy ()
f2 = mac . copy ()
for key in fp1 :
f1 [ key ] = fp1 [ key ]
for key in fp2 :
f2 [ key ] = fp2 [ key ]
f1 = list ( f1 . values ())
f2 = list ( f2 . values ())
braycurtis = scipy . spatial . distance . braycurtis ( f1 , f2 )
canberra = scipy . spatial . distance . canberra ( f1 , f2 )
chebyshev = scipy . spatial . distance . chebyshev ( f1 , f2 )
cityblock = scipy . spatial . distance . cityblock ( f1 , f2 )
correlation = scipy . spatial . distance . correlation ( f1 , f2 )
cosine = scipy . spatial . distance . cosine ( f1 , f2 )
euclidean = scipy . spatial . distance . euclidean ( f1 , f2 )
jensenshannon = scipy . spatial . distance . jensenshannon ( f1 , f2 )
minkowski = scipy . spatial . distance . minkowski ( f1 , f2 )
sqeuclidean = scipy . spatial . distance . sqeuclidean ( f1 , f2 )
wminkowski = scipy . spatial . distance . wminkowski ( f1 , f2 , 1 , np . ones ( len ( f1 )))
output_data = [ braycurtis ,
canberra ,
chebyshev ,
cityblock ,
correlation ,
cosine ,
euclidean ,
jensenshannon ,
minkowski ,
sqeuclidean ,
wminkowski ]
output_data = [ 0 if x != x else x for x in output_data ]
return output_data في هذه المهمة ، هناك فحوصات بصمات الأصابع لها إشارات RRSI من محيط WiFi Imitters في المركز التجاري. First Challange يريدنا أن نقدر المسافة بين بصمات الأصابع ، وهي مهمة الانحدار. استخدمنا آن (الشبكات العصبية الاصطناعية) مستوحاة من الشبكة العصبية البيولوجية. آن تتكون من ثلاث طبقات. طبقة الإدخال ، الطبقات المخفية (أكثر من واحدة) وطبقة الإخراج. تبدأ ANN بطبقة الإدخال التي تتضمن بيانات التدريب (مع الميزات) ، تمرر البيانات إلى الطبقة المخفية الأولى حيث يتم حساب البيانات بواسطة أوزان الطبقة المخفية الأولى. في الطبقات المخفية ، هناك تكرار لحساب الأوزان على المدخلات ثم تطبيقها وظيفة تنشيط [2]. نظرًا لأن مشكلتنا هي الانحدار ، فإن طبقتنا الأخيرة هي خلية عصبية مخرجات واحدة: ناتجها هو المسافات المتوقعة بين أزواج عمليات مسح البصمات. أول طبقة مخفية لدينا لديها 64 والثانية لديها 128 الخلايا العصبية. تتم مشاركة جميع الهندسة المعمارية لهذا النموذج على النحو التالي. 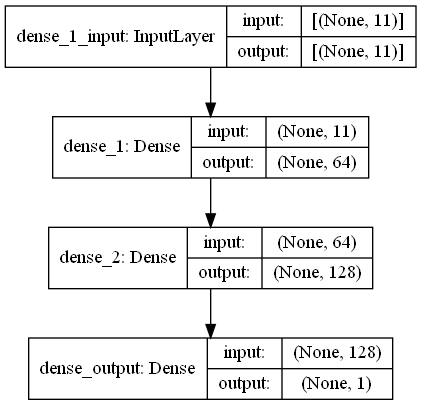
نقوم بإجراء التعلم العميق باستخدام وظيفتين. تشكل وظيفة create_model بيانات التدريب لتدريب النموذج وتحديد بنية النموذج. تنتج دالة model_features نموذجًا مع الهيكل المحدد. يتم حفظ النموذج الذي تم إنشاؤه لاستخدامه بعد تدريبه بواسطة وظيفة create_model .
## 1.5 Model
import scipy . spatial
import pandas as pd
import numpy as np
import matplotlib . pyplot as plt
from tensorflow import keras
from tensorflow . keras . models import Sequential
from tensorflow . keras . layers import Dense
#from keras.utils.vis_utils import plot_model
% matplotlib inline
def model_features ( i , ii ):
model = Sequential ()
model . add ( Dense ( i , input_shape = ( 11 , ), activation = 'relu' , name = 'dense_1' ))
model . add ( Dense ( ii , activation = 'relu' , name = 'dense_2' ))
model . add ( Dense ( 1 , activation = 'linear' , name = 'dense_output' ))
model . compile ( optimizer = 'adam' , loss = 'mse' , metrics = [ 'mae' ])
model . summary ()
#plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
#print(model.get_config())
return model
def create_model ( name ):
df = pd . read_csv ( name )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X )
y_train = np . array ( df [ df . columns [ - 1 ]])
model = model_features ( 64 , 128 )
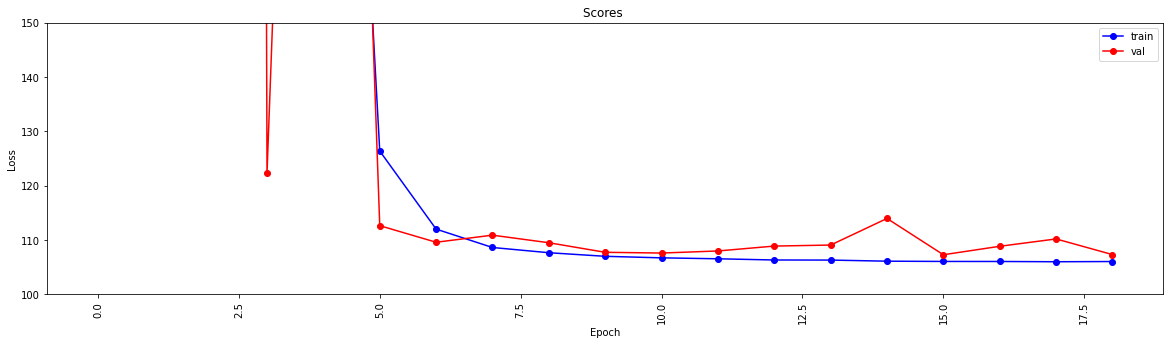
history = model . fit ( X_train , y_train , epochs = 19 , validation_split = 0.5 ) #,batch_size=1)
loss = history . history [ 'loss' ]
val_loss = history . history [ 'val_loss' ]
my_xticks = list ( range ( len ( loss )))
plt . figure ( figsize = ( 20 , 5 ))
plt . plot ( my_xticks , loss , linestyle = '-' , marker = 'o' , color = 'b' , label = "train" )
plt . plot ( my_xticks , val_loss , linestyle = '-' , marker = 'o' , color = 'r' , label = "val" )
plt . title ( "Scores " )
plt . legend ( numpoints = 1 )
plt . ylabel ( "Loss" )
plt . xlabel ( "Epoch" )
plt . xticks ( rotation = 90 )
plt . ylim ([ 100 , 150 ])
plt . show ()
madelname = "./THEMODEL"
model . save ( madelname )
print ( "Model Created!" )
تتحقق هذه الوظيفة إذا كانت بيانات التدريب والاختبار قد مرت من خلال استخراج الميزات. إذا لم يفعلوا ذلك ، فإنه ينشئ هذه الملفات والنموذج من خلال استدعاء الوظائف المقابلة. بعد التعامل مع النموذج وجميع استخراج الميزات ، يقوم بتنسيق بيانات الاختبار لإنتاج النتائج النهائية.
## 1.6 Checking the inputs
from numpy import inf
from numpy import nan
def create_new_files ( train , test ):
model_path = "./THEMODEL/"
my_train_file = 'new_train_features.csv'
my_test_file = 'new_test_features.csv'
if os . path . isfile ( my_train_file ) :
pass
else :
print ( "Please wait! Training data feature extraction is in progress... n it will take about 10 minutes" )
feature_extraction_file ( train , my_train_file , 1 )
print ( "TThe training feature extraction completed!!!" )
if os . path . isfile ( my_test_file ) :
pass
else :
print ( "Please wait! Testing data feature extraction is in progress... n it will take about 100-120 minutes" )
feature_extraction_file ( test , my_test_file , 0 )
print ( "The testing feature extraction completed!!!" )
if os . path . isdir ( model_path ):
pass
else :
print ( "Please wait! Creating the deep learning model... n it will take about 10 minutes" )
create_model ( my_train_file )
print ( "The model file created!!! n n n " )
model = keras . models . load_model ( model_path )
df = pd . read_csv ( my_test_file )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X_train = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X_train )
y_train = np . array ( df [ df . columns [ - 1 ]])
predicted = model . predict ( X_train )
print ( "Please wait! Creating resuşts... " )
return predicted تتميز هذه الخطوة بإجراء عمليات استخراج وإنشاء النماذج وتسمح لجميع العمليات بالبدء. لذلك ، باستخدام IDS من ملف test1_test.csv ، فإنه يملأ العمود الثالث (الإزاحة) مع المسافة المقدرة لأزواج البصمات هذه ويحفظ هذا الملف في الدليل مع اسم TASK1-MySubmission.csv .
## 1.7 Submission
distance_estimate = create_new_files ( train_data , test_ids )
count = 0
output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
output_data . append ([ id1 , id2 , distance_estimate [ count ][ 0 ]])
count += 1
print ( "Process finished. Preparing result file ..." )
with open ( "TASK1-MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )
print ( "The results are ready. n See MySubmission.csv" ) Please wait! Creating the deep learning model...
it will take about 10 minutes
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 64) 768
_________________________________________________________________
dense_2 (Dense) (None, 128) 8320
_________________________________________________________________
dense_output (Dense) (None, 1) 129
=================================================================
Total params: 9,217
Trainable params: 9,217
Non-trainable params: 0
_________________________________________________________________
Epoch 1/19
13748/13748 [==============================] - 30s 2ms/step - loss: 2007233.6250 - mae: 161.3013 - val_loss: 218.8822 - val_mae: 11.5630
Epoch 2/19
13748/13748 [==============================] - 27s 2ms/step - loss: 24832.6309 - mae: 53.9385 - val_loss: 123437.0859 - val_mae: 307.2885
Epoch 3/19
13748/13748 [==============================] - 26s 2ms/step - loss: 4028.0859 - mae: 29.9960 - val_loss: 3329.2024 - val_mae: 49.9126
Epoch 4/19
13748/13748 [==============================] - 27s 2ms/step - loss: 904.7919 - mae: 17.6284 - val_loss: 122.3358 - val_mae: 6.8169
Epoch 5/19
13748/13748 [==============================] - 25s 2ms/step - loss: 315.7050 - mae: 11.9098 - val_loss: 404.0973 - val_mae: 15.2033
Epoch 6/19
13748/13748 [==============================] - 26s 2ms/step - loss: 126.3843 - mae: 7.8173 - val_loss: 112.6499 - val_mae: 7.6804
Epoch 7/19
13748/13748 [==============================] - 27s 2ms/step - loss: 112.0149 - mae: 7.4220 - val_loss: 109.5987 - val_mae: 7.1964
Epoch 8/19
13748/13748 [==============================] - 26s 2ms/step - loss: 108.6342 - mae: 7.3271 - val_loss: 110.9016 - val_mae: 7.6862
Epoch 9/19
13748/13748 [==============================] - 26s 2ms/step - loss: 107.6721 - mae: 7.2827 - val_loss: 109.5083 - val_mae: 7.5235
Epoch 10/19
13748/13748 [==============================] - 27s 2ms/step - loss: 107.0110 - mae: 7.2290 - val_loss: 107.7498 - val_mae: 7.1105
Epoch 11/19
13748/13748 [==============================] - 29s 2ms/step - loss: 106.7296 - mae: 7.2158 - val_loss: 107.6115 - val_mae: 7.1178
Epoch 12/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.5561 - mae: 7.2039 - val_loss: 107.9937 - val_mae: 6.9932
Epoch 13/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.3344 - mae: 7.1905 - val_loss: 108.8941 - val_mae: 7.4530
Epoch 14/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.3188 - mae: 7.1927 - val_loss: 109.0832 - val_mae: 7.5309
Epoch 15/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.1150 - mae: 7.1829 - val_loss: 113.9741 - val_mae: 7.9496
Epoch 16/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.0676 - mae: 7.1788 - val_loss: 107.2984 - val_mae: 7.2192
Epoch 17/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0614 - mae: 7.1733 - val_loss: 108.8553 - val_mae: 7.4640
Epoch 18/19
13748/13748 [==============================] - 28s 2ms/step - loss: 106.0113 - mae: 7.1790 - val_loss: 110.2068 - val_mae: 7.6562
Epoch 19/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0519 - mae: 7.1791 - val_loss: 107.3276 - val_mae: 7.0981
INFO:tensorflow:Assets written to: ./THEMODELassets
Model Created!
The model file created!!!
Please wait! Creating resuşts...
100%|████████████████████████████████████████████████████████████████████| 5160445/5160445 [00:08<00:00, 610910.29it/s]
Process finished. Preparing result file ...
The results are ready.
See MySubmission.csv
بالنظر إلى أن لدينا الآن مقياسًا لتقييم مسافة واي فاي ، فإن مهمتنا التالية هي فصل المسارات من مركز تجاري (مركز تجاري مختلف إلى تلك المستخدمة في التحدي الأول!) في الأرضيات المنفصلة التي ينتمون إليها. يمكنك القيام بذلك بطرق مختلفة ، لكننا نقترح بشدة اتباع نهج تجميع الرسم البياني.
ضع في اعتبارك كل بصمة WiFi في البيانات كعقدة في رسم بياني ويمكننا تشكيل حافة مع بصمات أخرى في الرسم البياني من خلال تقييم التشابه أي بصمات الأصابع. يمكننا تعيين وزن كبير للحواف حيث لدينا تشابه كبير بين بصمات الأصابع والوزن المنخفض (أو بدون حافة) بين تلك التي لا تشبه. من الناحية النظرية ، فإن مقياس التشابه الدقيق تمامًا من شأنه أن يفصل طوابقًا تافهة حيث يمكننا استبعاد جميع حواف أكبر من حوالي 4 أمتار (حوالي ارتفاع 1 طابق من المبنى). في الواقع ، من المحتمل أننا سنقوم بعمل حواف زائفة بين الطوابق وسنحتاج إلى كسر هذه الحواف بطريقة ما.
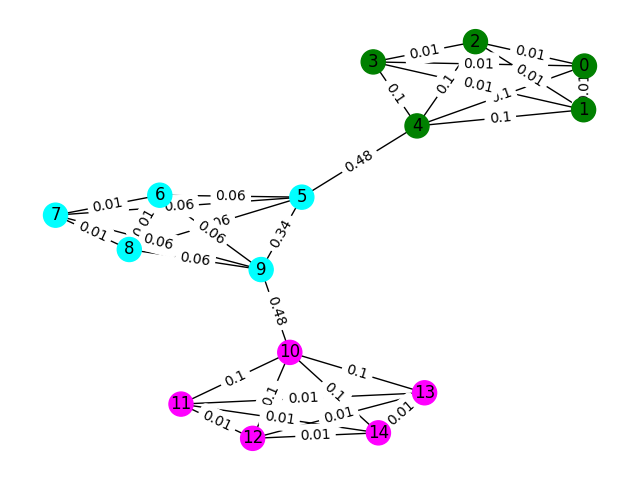
لنبدأ بمثال بسيط. ضع في اعتبارك الرسم البياني أدناه حيث تُظهر ألوان العقدة تصنيف الأرضيات الحقيقية لبصمات الأصابع وتعكس الحواف أننا نعتقد أن هذه العقد موجودة في نفس الطابق. بالنسبة لهذا التمرين ، قمنا بتسمية كل حافة مسبقًا بـ "بين النتيجة" ، وهو مقياس يحسب عدد المرات التي يتم فيها السير هذه الحافة عن طريق اتخاذ أقصر مسار بين أي عقدتين في الرسم البياني. عادة ، سيكشف هذا عن حواف تشير إلى اتصال عالي وقد يكون مرشحين للإزالة.
في هذا المثال ، استخدم درجة الحافة الفاصلة لاكتشاف Communties الرسم البياني. إرجاع قائمة من القوائم حيث يحتوي كل قائم فرعي على معرفات العقدة للمجتمعات. لاحظ أن هذا فقط للمساعدة في فهمك للمشكلة ولا يعتبر الحل الفعلي.
def detect_communities ( Graph ):
## This function should return a list of lists containing
## the node ids of the communities that you have detected.
eb_score = nx . edge_betweenness_centrality ( G )
raise NotImplementedError import networkx as nx
from metrics import check_result
G = nx . read_adjlist ( "graph.adjlist" )
communities = detect_communities ( G )
if check_result ( communities ):
print ( "Correct!" )
else :
print ( "Try again" ) بيانات تدريب العينة لهذه المشكلة هي مجموعة من البصمات 106981 ( task2_train_fingerprints.json ) وبعض الحواف بينهما. لقد قدمنا الملفات التي تشير إلى ثلاثة أنواع مختلفة من الحواف ، وينبغي التعامل معها بشكل مختلف.
task2_train_steps.csv يشير إلى الحواف التي تربط الخطوات اللاحقة داخل مسار. يجب أن تكون هذه الحواف موثوقة للغاية لأنها تشير إلى اليقين بأن بصمات أصابع تم تسجيلها من نفس الطابق.
task2_train_elevations.csv تشير إلى عكس الخطوات. تشير هذه الارتفاعات إلى أن بصمات الأصابع هي بالتأكيد من طابق مختلف. يمكنك بالتالي استقراء ذلك إذا كانت بصمة
task2_train_estimated_wifi_distances.csv هي المسافات التي تم حسابها مسبقًا والتي قمنا بحسابها باستخدام مقياس المسافة الخاص بنا. هذا المقياس غير كامل ، وبالتالي نحن نعلم أن العديد من هذه الحواف ستكون غير صحيحة (أي أنها سوف تربط طابقين معًا). نقترح أن تستخدم الحواف في هذا الملف في البداية لإنشاء الرسم البياني الأولي وحساب بعض الحلول. ومع ذلك ، إذا حصلت على درجة عالية على Task1 ، فقد تفكر في حساب مسافات WiFi الخاصة بك لإنشاء رسم بياني.
يمكن أن يكون الرسم البياني الخاص بك في أحد مستويي التفاصيل ، إما مستوى المسار أو مستوى بصمات الأصابع ، يمكنك اختيار التمثيل الذي تريد استخدامه ، ولكن في النهاية نريد أن نعرف مجموعات المسار . سيكون لمستوى المسار كل عقدة كمسار وتحدث حواف بين العقد إذا كانت بصمات الأصابع في مساراتها عالية. سيكون لمستوى بصمة البصمة كل بصمة كعقدة. يمكنك البحث في معرف المسار لبصمة بصمة باستخدام task2_train_lookup.json للتحويل بين العروض.
لمساعدتك في تصحيح وتدريب الحل الخاص بك ، قدمنا حقيقة أرضية لبعض المسارات في task2_train_GT.json . في هذا الملف ، تكون المفاتيح هي معرفات المسار (كما هو الحال في task2_train_lookup.json ) والقيم هي معرف الأرضية الحقيقي للمبنى.
مجموعة الاختبار هي نفس التنسيق تمامًا مثل مجموعة التدريب (لمبنى منفصل ، لن نجعل الأمر بهذه السهولة ؛)) لكننا لم ندرج ملف الحقيقة الأرضية المكافئة. سيتم حجب هذا للسماح لنا بتسجيل الحل الخاص بك.
تشير إلى النظر
في هذا القسم ، سنقدم بعض رمز المثال لفتح الملفات وبناء كلا النوعين من الرسم البياني.
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/train"
with open ( os . path . join ( path_to_data , "task2_train_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_train_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_train_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_train_lookup.json" )
gt_path = os . path . join ( path_to_data , "task2_train_GT.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f )
with open ( gt_path ) as f :
gt = json . load ( f )
هذه طريقة واحدة لبناء الرسم البياني على مستوى البصمات ، حيث كل عقدة في الرسم البياني هي بصمة. لقد أضفنا الأوزان الحافة التي تتوافق مع المسافات المقدرة/الحقيقية من حواف WiFi و PDR على التوالي. لقد أضفنا أيضًا حواف الارتفاع للإشارة إلى هذه العلاقة. قد ترغب في إنفاذ صراحة أنه لا يوجد أي من هذه الحواف (أو أي حافة ارتفاع صالحة بين المسارات) عند تطوير الحل الخاص بك.
G = nx . Graph ()
for id1 , id2 , dist in tqdm ( steps ):
G . add_edge ( id1 , id2 , ty = "s" , weight = dist )
for id1 , id2 , dist in tqdm ( wifi ):
G . add_edge ( id1 , id2 , ty = "w" , weight = dist )
for id1 , id2 in tqdm ( elevs ):
G . add_edge ( id1 , id2 , ty = "e" )يمكن القول إن الرسم البياني للمسار ليس بسيطًا كما تحتاج إلى التفكير في طريقة لتمثيل العديد من اتصالات WiFi بين المسارات. في مثال الرسم البياني أدناه ، نأخذ المسافة المتوسطة كوزن ، ولكن هل هذا هو أفضل تمثيل؟
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])يجب أن يكون تقديمك ملفًا لـ CSV حيث تكون المسارات التي تعتقد أنها في نفس الطابق لديها فهرسها على نفس الصف الذي يفصله الفواصل. سيتم إدخال كل مجموعة جديدة في صف جديد.
على سبيل المثال ، انظر الإدخال العشوائي أدناه.
import random
random_data = []
n_clusters = random . randint ( 50 , 100 )
for i in range ( 0 , n_clusters ):
random_data . append ([])
for traj in set ( fp_lookup . values ()):
cluster = random . randint ( 0 , n_clusters - 1 )
random_data [ cluster ]. append ( traj )
with open ( "MyRandomSubmission.csv" , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( random_data )يمكن تلخيص الخطوات في المهمة 2 على النحو التالي:
Node2vec .TASK2-Mysubmission.csv ) وفقًا لمسار IDS.تم توضيح هذه الخطوات في الصورة أدناه.

استخدمنا Python 3.6.5 لإنشاء ملف التطبيق. قمنا بتضمين بعض الوحدات الإضافية التي لم يتم تضمينها في ملف المثال المقدم في بداية المنافسة. يمكن إدراج هذه الوحدات النمطية على النحو التالي:
| الأذواق | مهمة |
|---|---|
| Scikit-Learn | التعلم الآلي وإعداد البيانات |
| Node2Vec | تعلم ميزة قابلة للتطوير للشبكات |
| numpy | العمليات الرياضية |
بدأنا بتركيب هذه الوحدات كخطوة أولى.
## 2.1 Installing modules
!p ip install node2vec
!p ip install scikit - learn
!p ip install numpy في هذه الخطوة ، قمنا بإصلاح البذور العشوائية ذات الصلة لاستخدامها من أجل الحصول على نتائج قابلة للتكرار. وبهذه الطريقة ، قدمنا مسارًا حتميًا حيث نحصل على نفس النتيجة في كل تشغيل. ومع ذلك ، وفقًا لملاحظاتنا ، قد تختلف النتائج التي تم الحصول عليها على أجهزة الكمبيوتر المختلفة قليلاً (± 1 ٪)
## 2.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )في هذا القسم ، يتم تحميل الملفات المقدمة لبيانات الاختبار.
wifi معرفات وأوزان من task2_test_estimated_wifi_distances.csv .steps متغير يأخذ المعرفات والأوزان من ملف task2_test_steps.csv .elevs IDS من File task2_test_elevations.csv .fp_lookup على معرفات ومسارات من ملف task2_test_lookup.json . لم نفضل طريقة إعادة حساب المسافات المقدرة الواردة في WiFi مع النموذج الذي حصلنا عليه في Task1 ، لأن النتائج التي حصلنا عليها من هذه العملية لم تحدث فرقًا كبيرًا. لهذا السبب لم نستخدم ملف task2_test_fingerprints.json في عملنا النهائي.
## 2.3 Loading the data
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/test"
with open ( os . path . join ( path_to_data , "task2_test_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_test_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_test_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_test_lookup.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f ) 3773297it [00:19, 191689.25it/s]
2767it [00:00, 52461.27it/s]
139537it [00:00, 180082.01it/s]
نأخذ المسافة المتوسطة كوزن عند إنشاء الرسم البياني للمسار. استخدمنا المثال المقدم للمهمة 2 ( Task2-IPS-Challenge-2021.ipynb ) لهذه العملية. لقد أنقذنا الرسم البياني الناتج ( B ) كقائمة مجاورة في الدليل (مثل my.adjlist ).
## 2.3 Generating the Trajectory graph.
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])
nx . write_adjlist ( B , "my.adjlist" ) 100%|████████████████████████████████████████████████████████████████████| 3773297/3773297 [00:27<00:00, 135453.95it/s]
100%|██████████████████████████████████████████████████████████████████████████████████████| 2767/2767 [00:00<?, ?it/s]
قبل إعطاء قائمة المجاورة كمدخلات لخوارزميات التعلم الآلي ، نقوم بتحويل العقد إلى المتجه. في عملنا ، استخدمنا Node2VEC كطاقة خوارزمية تضمين الرسم البياني الذي اقترحه Grover & Leskovec في عام 2016 [3]. Node2Vec هي خوارزمية شبه خاضعة للإشراف لتعلم العقد في الشبكة. يتم إنشاء Node2Vec استنادًا إلى تقنية Skip-Gram ، وهو نهج NLP محفز على مفهوم بنية التوزيع. تستخدم تقنية Skip-Gram Word المركزية (إدخال) للتنبؤ بالجيران (الإخراج) أثناء حساب احتمالات المحيطات بناءً على حجم نافذة معين (تسلسل متجاور للعناصر قبل بعد المركز) ، وبعبارة أخرى n-grams. على عكس نهج NLP ، لا يتم تغذية نظام Node2VEC بالكلمات التي لها بنية خطية ، ولكن العقد والحواف ، التي لها بنية رسومية موزعة. هذا الهيكل متعدد الأبعاد يجعل التضمينات معقدة ومكلفة من الناحية الحسابية ، ولكن Node2VEC يستخدم أخذ العينات السلبية مع تحسين النسب التدريجي العشوائي (SGD) للتعامل معها. بالإضافة إلى ذلك ، يتم استخدام نهج المشي العشوائي للكشف عن العينة المجاورة للعينة من العقدة المصدر في بنية غير خطية.
في دراستنا ، أجرينا أولاً تمثيل المتجه لعلاقات العقدة في الفضاء المنخفض الأبعاد عن طريق النمذجة باستخدام Node2Vec من مسافة معينة من العقد (الأوزان). ثم استخدمنا إخراج Node2Vec (التضمينات الرسم البياني) ، الذي يحتوي على متجهات من العقد ، لتغذية خوارزمية التجميع التقليدية.
يمكن إدراج المعلمات التي نستخدمها في NOD2VEC على النحو التالي:
| مقياس البارامير | قيمة |
|---|---|
| أبعاد | 32 |
| walk_length | 15 |
| num_walks | 100 |
| العمال | 1 |
| البذور | 0 |
| نافذة | 10 |
| min_count | 1 |
| batch_words | 4 |
يأخذ نموذج Node2Vec قائمة المجاورة كمدخلات ويخرج متجهًا بحجم 32. في هذا الجزء ، يتم إنشاء ملف Node.py وتشغيله في Jupyter Notebook . هناك سببان يفضل تشغيله خارجيًا بدلاً من خلية دفتر الملاحظات Jupyter.
Node2vec هي طريقة باهظة الثمن من الناحية الحسابية ، فإن خطأ RAM Overflow ممكن تمامًا إذا تم تشغيله داخل دفتر Jupyter. إنشاء وتشغيل نموذج Node2vec في الخارج يتجنب هذا الخطأ. تقوم الخلية أدناه بإنشاء الملف المسماة Node.py. هذا الملف ينشئ نموذج Node2Vec. يأخذ هذا النموذج قائمة المجاورة ( my.adjlist ) كمدخل وإنشاء ملف متجه 32 أبعاد كإخراج ( vectors.emb ).
مهم! يجب تشغيل الرمز أدناه في توزيعات Linux (تم اختبارها في Google Colab و Ubuntu).
# 2.4 Converting nodes to vectors
# A folder named tmp is created. This folder is essential for the node2vec model to use less RAM.
try :
if not os . path . exists ( "tmp" ):
os . makedirs ( "tmp" )
except OSError :
print ( "The folder could not be created! n Please manually create the " tmp " folder in the directory" )
node = """
# importing related modules
from node2vec import Node2Vec
import networkx as nx
#importing adjacency list file as B
B = nx.read_adjlist("my.adjlist")
seed_value=0
# Specifying the input and hyperparameters of the node2vec model
node2vec = Node2Vec(B, dimensions=32, walk_length=15, num_walks=100, workers=1,seed=seed_value,temp_folder = './tmp')
#Assigning/specifying random seeds
import os
os.environ['PYTHONHASHSEED']=str(seed_value)
import random
random.seed(seed_value)
import numpy as np
np.random.seed(seed_value)
# creation of the model
model = node2vec.fit(window=10, min_count=1, batch_words=4,seed=seed_value)
# saving the output vector
model.wv.save_word2vec_format("vectors.emb")
# save the model
model.save("vectorMODEL")
"""
f = open ( "node.py" , "w" )
f . write ( node )
f . close ()
! PYTHONHASHSEED = 0 python3 node . py بعد إنشاء ملف المتجه الخاص بنا ، نقرأ هذا الملف ( vectors.emb ). يتكون هذا الملف من 33 عمودًا. العمود الأول هو رقم العقدة (IDS) ، وتبقى قيم متجه. عن طريق فرز الملف بأكمله حسب العمود الأول ، نقوم بإرجاع العقد إلى طلبها الأصلي. ثم نحذف عمود المعرف هذا ، والذي لن نستخدمه بعد الآن. لذلك ، نعطي الشكل النهائي لبياناتنا. بياناتنا جاهزة للاستخدام في تطبيقات التعلم الآلي.
# 2.4 Reshaping data
vec = np . loadtxt ( "vectors.emb" , skiprows = 1 )
print ( "shape of vector file: " , vec . shape )
print ( vec )
vec = vec [ vec [:, 0 ]. argsort ()];
vec = vec [ 0 : vec . shape [ 0 ], 1 : vec . shape [ 1 ]] shape of vector file: (11162, 33)
[[ 9.1200000e+03 3.9031842e-01 -4.7147268e-01 ... -5.7490986e-02
1.3059708e-01 -5.4280665e-02]
[ 6.5320000e+03 -3.5591956e-02 -9.8558587e-01 ... -2.7217887e-02
5.6435770e-01 -5.7787680e-01]
[ 5.6580000e+03 3.5879680e-01 -4.7564098e-01 ... -9.7607370e-02
1.5506668e-01 1.1333219e-01]
...
[ 2.7950000e+03 1.1724627e-02 1.0272172e-02 ... -4.5596390e-04
-1.1507459e-02 -7.6738600e-04]
[ 4.3380000e+03 1.2865483e-02 1.2103912e-02 ... 1.6619096e-03
1.3672550e-02 1.4605848e-02]
[ 1.1770000e+03 -1.3707868e-03 1.5238028e-02 ... -5.9994194e-04
-1.2986251e-02 1.3706315e-03]]
Task-2 هي مشكلة تجميع. الفرضية التي نحتاج إلى تحديدها عند حل هذه المشكلة هي عدد المجموعات التي يجب أن نقسمها. لهذا ، جربنا أرقام مجموعات مختلفة وقارننا الدرجات التي حصلنا عليها. يوضح الرسم البياني أدناه مقارنة عدد المجموعات والنتيجة التي تم الحصول عليها. كما يتضح من هذا الرسم البياني ، زاد عدد المجموعات بشكل مستمر بين 5 و 21 ، مع بعض تقلبات الاستثناء ، واستقرت بعد 21. لهذا السبب ، ركزنا على عدد المجموعات بين 21 و 23 في دراستنا.
# 2.5 Determine the number of clusters
import numpy as np
import matplotlib . pyplot as plt
import seaborn as sns
import matplotlib
% matplotlib inline
sns . set_style ( "whitegrid" )
agglom = [ 24.69 , 28.14 , 28.14 , 28.14 , 30 , 33.33 , 40.88 , 38.70 , 40 , 40 , 40 , 29.12 , 45.85 , 45.85 , 48.00 , 50.17 , 57.83 , 57.83 , 57.83 ]
plt . figure ( figsize = ( 10 , 5 ))
plt . plot ( range ( 5 , 24 ), agglom )
matplotlib . pyplot . xticks ( range ( 5 , 24 ))
plt . title ( 'Number of clusters and performance relationship' )
plt . xlabel ( 'Number of clusters' )
plt . ylabel ( 'Score' )
plt . show ()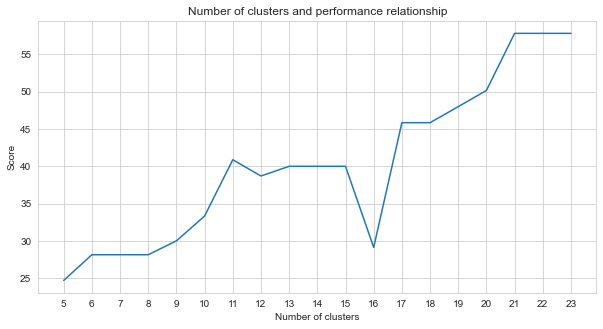
من بين أساليب التعلم الآلي غير الخاضعة للإشراف التي جربناها (مثل K-Means ، التجميع التكتل ، انتشار التقارب ، متوسط التحول ، التجميع الطيفي ، DBSCAN ، البصريات ، البتولا ، K-Mini-Batch Means) ، حققنا أفضل النتائج باستخدام K-Means مع 23 مجموعة.
K-Means هي خوارزمية التجميع هي واحدة من تقنيات التعلم الآلي الأساسي والتقليدي غير الخاضع للإشراف والتي تجعل الافتراضات لإيجاد مجموعات متجانسة أو طبيعية من العناصر (مجموعات) باستخدام بيانات غير مخصصة. يجب على المجموعات تعيين نقاط (العقد في بياناتنا) التي تم تجميعها معًا والتي تشترك في أوجه تشابه معينة. يحتاج K-Means إلى العدد المستهدف من النطاقات الوسطى التي تشير إلى عدد المجموعات التي يجب تقسيم البيانات إليها. تبدأ الخوارزمية بمجموعة من النطاقات النقطية المعينة عشوائياً ثم تواصل التكرارات للعثور على أفضل المواقف منها. تقوم الخوارزمية بتعيين النقاط/العقد إلى النطاقات النطوية المعينة باستخدام مجموع مربعات العضو في النقاط ، وهذا يستمر في التحديث والانتقال [4]. في مثالنا ، يعكس عدد الأوسط عدد الأطراف. تجدر الإشارة إلى أن هذا لا يوفر معلومات حول ترتيب الأرضيات.
أدناه ، تم تقديم تطبيق K-mean لـ 23 مجموعة.
# 2.5 Best result
from sklearn import cluster
import time
ML_results = []
k_clusters = 23
algorithms = {}
algorithms [ 'KMeans' ] = cluster . KMeans ( n_clusters = k_clusters , random_state = 10 )
second = time . time ()
for model in algorithms . values ():
model . fit ( vec )
ML_results = list ( model . labels_ )
print ( model , time . time () - second ) KMeans(n_clusters=23, random_state=10) 1.082334280014038
يحدد إخراج خوارزمية التعلم الآلي التي تتجمع بصمات الأصابع التي تنتمي إليها. ولكن ما هو مطلوب منا هو تجميع المسارات. لذلك ، يتم تحويل بصمات الأصابع هذه إلى نظرائهم في المسار باستخدام متغير fp_lookup . تتم معالجة هذا الإخراج في ملف TASK2-Mysubmission.csv .
## 2.6 Submission
result = {}
for ii , i in enumerate ( set ( fp_lookup . values ())):
result [ i ] = ML_results [ ii ]
ters = {}
for i in result :
if result [ i ] not in ters :
ters [ result [ i ]] = []
ters [ result [ i ]]. append ( i )
else :
ters [ result [ i ]]. append ( i )
final_results = []
for i in ters :
final_results . append ( ters [ i ])
name = "TASK2-Mysubmission.csv"
with open ( name , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( final_results )
print ( name , "file is ready!" ) TASK2-Mysubmission.csv file is ready!
[1] P. Virtanen و Scipy 1.0 المساهمين. Scipy 1.0: الخوارزميات الأساسية للحوسبة العلمية في بيثون. طرق الطبيعة ، 17: 261--272 ، 2020.
[2] أ. جيرون ، التعلم الآلي العملي مع Scikit-Learn ، Keras ، و TensorFlow: المفاهيم والأدوات والتقنيات لبناء أنظمة ذكية. O'Reilly Media ، 2019
[3] A. Grover ، J. Leskovec. مؤتمر ACM SIGKDD الدولي لاكتشاف المعرفة واستخراج البيانات (KDD) ، 2016.
[4] Jin X. ، Han J. (2011) K-Means Clustering. In: Sammut C. ، Webb GI (eds) Encyclopedia of Machine Learning. سبرينغر ، بوسطن ، ماجستير. https://doi.org/10.1007/978-0-387-30164-8_425