equivalence testing multiple regression

اختبار التكافؤ للانحدار المتعدد

يمكن تطبيق اختبار التكافؤ لتقييم ما إذا كان التأثير الملحوظ من المتنبئ الفردي في نموذج الانحدار المتعدد صغيرًا بما يكفي ليتم اعتباره ضئيلاً إحصائياً وعملياً (Alter & Counsell ، 2021). لمزيد من المعلومات ، يرجى الرجوع إلى صفحة OSF و/أو preprint المتاحة بحرية على psyarxiv.

توفر الوظائف التالية بدائل مناسبة قائمة على التكافؤ للاختتام تأثير ضئيل بين المتنبئ والنتائج في الانحدار المتعدد

تم تصميم وظائف R هذه لاستيعاب سياقات بحث متعددة دون عناء ، مع أو بدون الوصول إلى مجموعة البيانات الكاملة. توفر وظيفتان ، reg.equiv.fd() و reg.equiv() ، إخراج مماثل ولكنهما يختلفان في نوع معلومات الإدخال المطلوبة من قبل المستخدم.

على وجه التحديد ، تتطلب الوظيفة الأولى ، reg.equiv.fd() ، مجموعة البيانات والنموذج الكامل في R (كائن lm ) ، في حين أن الثانية لا. إن reg.equiv() مخصص للباحثين الذين لا يستطيعون الوصول إلى مجموعة البيانات الكاملة ولكنهم لا يزالون يرغبون في تقييم افتقار تنبؤ معين إلى الارتباط بمتغير النتائج في الانحدار المتعدد ، على سبيل المثال ، باستخدام المعلومات المعروضة عادة في قسم النتائج أو تم الإبلاغ عن الجدول في مقالة منشورة.

reg.equiv.fd() : مجموعة بيانات كاملة مطلوبة

المدخلات المطلوبة :

• datfra= إطار بيانات (على سبيل المثال ، MTCars)
• model= النموذج ، كائن LM (على سبيل المثال ، mod1 ، حيث mod1<- mpg~hp+cyl )
• delta= أصغر حجم تأثير الفائدة (SESOI) ، حجم التأثير ذي معنى الحد الأدنى (MMEs) ، أو الحد الأعلى لفاصل التكافؤ (؟) (على سبيل المثال ، .15)
• predictor= اسم المتنبئ ليتم اختباره (على سبيل المثال ، "cyl" )

الإعدادات الافتراضية:

• يتم تعيين نوع test= نوع الاختبار تلقائيًا على اختبارين من جانب واحد (Tost ؛ Schuirmann ، 1987) ، والخيار الآخر هو Anderson-Hauck (Ah ؛ Anderson & Hauck ، 1983)
• std= الدلتا (أو ، sesoi) هو تعيين موحد بشكل افتراضي. أشر إلى std=FALSE لافتراض وحدات غير قياسية
• alpha= يتم تعيين معدل الخطأ من النوع الاسمي الأول إلى .05 بشكل افتراضي. للتغيير ، ببساطة الإشارة إلى مستوى ألفا. على سبيل المثال ، alpha=.10

reg.equiv.fd() مثال: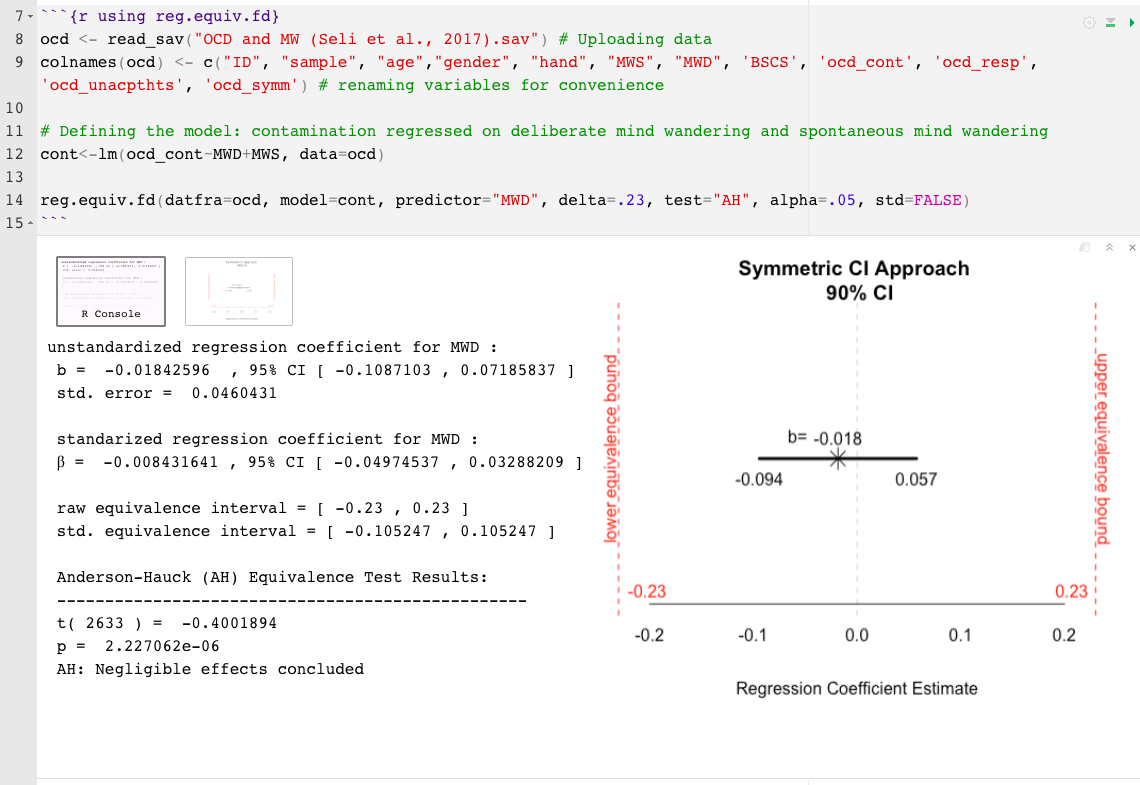

reg.equiv() : مجموعة بيانات كاملة غير مطلوبة

المدخلات المطلوبة :

• b= حجم التأثير المقدر المرتبط بالتنبؤ بالاهتمام ، يمكن أن يكون هذا إما موحد أو غير قياسي (على سبيل المثال ، .02)
• se= الخطأ القياسي المرتبط بحجم تأثير المتنبأ بالاهتمام (إذا كان حجم التأثير موحدًا ، فتأكد من أن قيمة se مرتبطة بالموحد وليس التأثير الخام)
• p= عدد إجمالي المتنبئين في نموذج الانحدار (باستثناء التقاطع)
• n= حجم العينة
• delta= أصغر حجم تأثير الفائدة (SESOI) ، حجم التأثير ذي معنى الحد الأدنى (MMEs) ، أو الحد الأعلى لفاصل التكافؤ (؟) (على سبيل المثال ، .15)
• predictor= اسم المتنبئ ليتم اختباره (على سبيل المثال ، "cyl" )

الإعدادات الافتراضية:

• يتم تعيين نوع test= نوع الاختبار تلقائيًا على اختبارين من جانب واحد (Tost ؛ Schuirmann ، 1987) ، والخيار الآخر هو Anderson-Hauck (Ah ؛ Anderson & Hauck ، 1983)
• std= يتم تعيين دلتا (أو ، sesoi) وحجم التأثير المشار إليه على أنه موحد بشكل افتراضي. أشر إلى std=FALSE لافتراض وحدات غير قياسية
• alpha= يتم تعيين معدل الخطأ من النوع الاسمي الأول إلى .05 بشكل افتراضي. للتغيير ، ببساطة الإشارة إلى مستوى ألفا. على سبيل المثال ، alpha=.10

reg.equiv() مثال: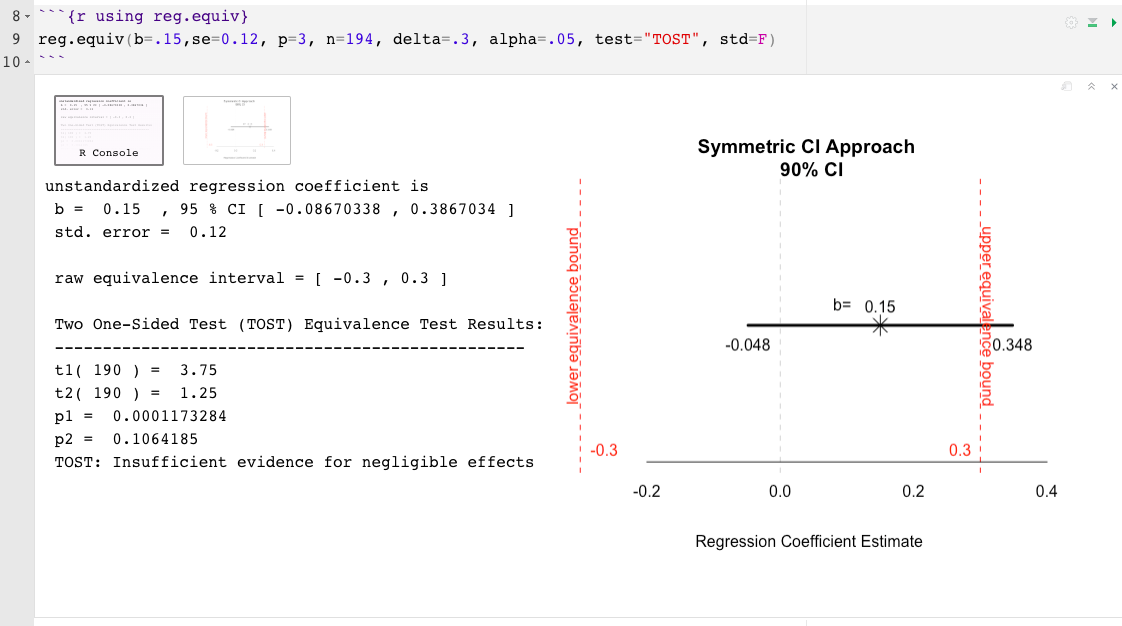

توصيات لتفسير نتائج الاختبار

اختبار التكافؤ هو طريقة مصممة ضمن إطار اختبار أهمية الفئة الخالية (NHST). تم انتقاد NHST بشكل كبير بسبب إفراطه في الاعتماد على النتائج ثنائية التفرع لقيم P مع القليل من الأثر ، أو عدم وجود أي اعتبار لحجم التأثير أو آثاره في الممارسة (على سبيل المثال ، Cumming ، 2012 ؛ Fidler & Loftus ، 2009 ؛ Harlow ، 1997 ؛ Kirk ، 2003 ؛ لي ، 2016 2014). يجب أن يدرك الباحثون حدود NHST ، ويفصلون الجوانب العملية والإحصائية لنتائج الاختبار.

لتقليل القيود المفروضة على قيم P ، من المفيد تفسير حجم التأثير الملحوظ ودقة ما بعد ختام "التأثيرات الضئيلة" أو "أدلة غير كافية للتأثيرات الضئيلة". يجب تفسير التأثيرات المرصودة فيما يتعلق بحدود التكافؤ ، ومدى عدم اليقين ، وآثارها العملية (أو عدم وجودها) . لهذا السبب ، تتضمن وظيفتي R المقدمة هنا أيضًا تمثيلًا رسوميًا للتأثير المرصود وعدم اليقين المرتبط به فيما يتعلق بفاصل التكافؤ. إن المؤامرة الناتجة تساعد في توضيح مدى قربها أو بعيدة أو واسعة أو ضيقة التأثير المرصود وهامش الخطأ من حدود التكافؤ ؛ الاستنتاج حول نسبة وموضع نطاق الثقة فيما يتعلق بفاصل التكافؤ يمكن أن يساعد في تفسير النتائج علاوة على قيم p .

لمراجعة الأدب المتعمقة ، و shucssion ، والتوصيات ، والدروس التعليمية التفصيلية ، يرجى الرجوع إلى Alter & Counsell (2021).

مراجع

1. Alter ، U. ، & Counsell ، A. (2021 ، 17 يونيو). اختبار التكافؤ للانحدار المتعدد . https://doi.org/10.17605/osf.io/w96xe
2. Anderson ، S. ، & Hauck ، WW (1983). إجراء جديد لاختبار معادلة في التوافر البيولوجي المقارن والتجارب السريرية الأخرى. الإحصاءات والاتصالات النظرية والأساليب ، 12 ، 2663-2692. https://doi.org/10.1080/03610928308828634
3. Cumming ، G. (2012). فهم الإحصاءات الجديدة: أحجام التأثير ، فترات الثقة ، والتحليل التلوي . نيويورك ، نيويورك: مجموعة تايلور وفرانسيس ، LLC
4. Cumming ، G. (2014). الإحصاءات الجديدة: لماذا وكيف. العلوم النفسية ، 25 (1) ، 7-29. https://doi.org/10.1177/0956797613504966
5. Fidler ، F. ، & Loftus ، G. (2009). لماذا يجب أن تحل الأرقام مع أشرطة الخطأ محل قيم p: بعض الوسائط المفاهيمية والمظاهرات التجريبية. Zeitschrift Für Psychologie/Journal of Psychology ، 217 (1) ، 27-37. https://doi.org/10.1027/0044-3409.217.1.27
6. Harlow ، LL (1997). اختبار الأهمية في مقدمة ونظرة عامة . في LL Harlow ، SA Muliak & JH Steiger (Eds.). ماذا لو لم تكن هناك اختبارات أهمية؟ (pp.1-17). ماهواه ، نيوجيرسي ، الولايات المتحدة الأمريكية: لورانس إرلبوم.
7. Hauck ، WW ، & Anderson ، S. (1984). إجراء إحصائي جديد لاختبار معادلة في تجارب التوافر البيولوجي المقارنان. Journal of Pharmacokinetics and Biopharmaceutics ، 12 (1) ، 83-91. https://doi.org/10.1007/BF01063612
8. كيرك ، ري (2003). أهمية حجم التأثير . في SF Davis (ed.) ، كتيب أساليب البحث في علم النفس التجريبي (ص. 83-105). مالدن ، ماساتشوستس: بلاكويل.
9. لي ، DK (2016). بدائل لقيمة P: فاصل الثقة وحجم التأثير. المجلة الكورية للتخدير ، 69 (6) ، 555-562. https://doi.org/10.4097/kjae.2016.69.6.555
10. شويرمان ، دي جي (1987). مقارنة بين إجراء الاختبارين أحادي الجانب ونهج الطاقة لتقييم معادلة متوسط ​​التوافر البيولوجي. مجلة الحرائك الدوائية والركض الحيوي ، 15 ، 657-680. https://doi.org/10.1007/BF01068419
11. Seli ، P. ، Risko ، EF ، Purdon ، C. ، & Smilek ، D. (2017). الأفكار المتطفلة: ربط العقل العفوي بالتجول وأعراض الوسواس القهري. البحوث النفسية ، 81 (2) ، 392-398. https://doi.org/10.1007/S00426-016-0756-3!