

Das Paket FRK ist auf CRAN verfügbar! Zur Installation geben Sie bitte ein
install.packages( " FRK " ) Um die neueste Entwicklungsversion zu installieren, laden Sie bitte devtools und geben Sie Folgendes ein
install_github( " andrewzm/FRK " , dependencies = TRUE , build_vignettes = TRUE )Ein Papier zur Einführung des Pakets finden Sie hier. Ein Artikel, der den Ansatz in einer nicht-Gaußschen Umgebung detailliert beschreibt, ist hier verfügbar (eine sechsseitige Zusammenfassung dieses Artikels finden Sie hier).
Die Vignette „FRK_intro“ fasst das Paket zusammen, enthält Einzelheiten zum EM-Algorithmus, der in einer Gaußschen Umgebung verwendet werden kann, und enthält mehrere Beispiele. Eine weitere Vignette, „FRK_non-Gaussian“, fasst die Schlussfolgerung in einer nicht-Gaußschen Umgebung (wo eine Laplace-Näherung verwendet wird) zusammen und enthält Beispiele mit nicht-Gaußschen Daten und den neu verfügbaren Darstellungsmethoden. Um zu den Vignetten zu gelangen, klicken Sie bitte auf die folgenden Links:
Einführung in FRK
Tutorial zur Modellierung räumlicher und räumlich-zeitlicher nicht-Gaußscher Daten mit FRK
Eine pkgdown Seite ist auch hier verfügbar.
Wenn Sie FRK in Ihrer Arbeit, Forschung oder anderen Aktivitäten verwenden, zitieren Sie es bitte unter Verwendung der von citation("FRK") bereitgestellten Informationen.
Paket: FRK
Typ: Paket
Titel: Fixed Rank Kriging
Version: 2.3.1
Datum: 16.07.2024
Autor: Andrew Zammit-Mangion, Matthew Sainsbury-Dale
Betreuer: Andrew Zammit-Mangion [email protected]
Beschreibung: Ein Tool zur räumlichen/räumlich-zeitlichen Modellierung und Vorhersage mit großen Datensätzen. Der Ansatz modelliert das Feld und damit die Kovarianzfunktion mithilfe einer Reihe von Basisfunktionen. Diese Basisfunktionsdarstellung mit festem Rang erleichtert die Modellierung großer Datenmengen, und die Methode ermöglicht natürlich instationäre, anisotrope Kovarianzfunktionen. Die Diskretisierung des räumlichen Bereichs in sogenannte Basic Areal Units (BAUs) erleichtert die Verwendung von Beobachtungen mit unterschiedlicher Unterstützung (dh sowohl punktbezogener als auch flächenbezogener Unterstützung, möglicherweise gleichzeitig) und die Vorhersage über beliebige, vom Benutzer angegebene Regionen. FRK unterstützt auch die Inferenz über verschiedene Mannigfaltigkeiten, einschließlich der 2D-Ebene und der 3D-Kugel, und bietet Hilfsfunktionen zum relativ einfachen Modellieren, Anpassen, Vorhersagen und Plotten. Version 2.0.0 und höher unterstützt auch die Modellierung von nicht-Gaußschen Daten (z. B. Poisson-, Binomial-, Negativ-Binomial-, Gamma- und invers-Gaußsche Daten) durch Verwendung eines verallgemeinerten linearen gemischten Modells (GLMM)-Frameworks. Zammit-Mangion und Cressie (2021) beschreiben FRK in einer Gaußschen Umgebung und beschreiben detailliert die Verwendung von Basisfunktionen und BAUs, während Sainsbury-Dale et al. (2024) beschreiben FRK in einer nicht-Gaußschen Umgebung; Es sind zwei Vignetten verfügbar, die diese Arbeiten zusammenfassen und zusätzliche Beispiele liefern.
Lizenz: GPL (>= 2)
library( " FRK " )
library( " sp " )
library( " ggplot2 " )
library( " ggpubr " )
# # Setup
m <- 1000 # Sample size
RNGversion( " 3.6.0 " ); set.seed( 1 ) # Fix seed
zdf <- data.frame ( x = runif( m ), y = runif( m )) # Generate random locs
zdf $ z <- sin( 8 * zdf $ x ) + cos( 8 * zdf $ y ) + 0.5 * rnorm( m ) # Simulate data
coordinates( zdf ) = ~ x + y # Turn into sp object
# # Run FRK
S <- FRK( f = z ~ 1 , # Formula to FRK
list ( zdf ), # All datasets are supplied in list
n_EM = 10 ) # Max number of EM iterations
pred <- predict( S ) # Prediction stage
# # Plotting
plotlist <- plot( S , pred )
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )
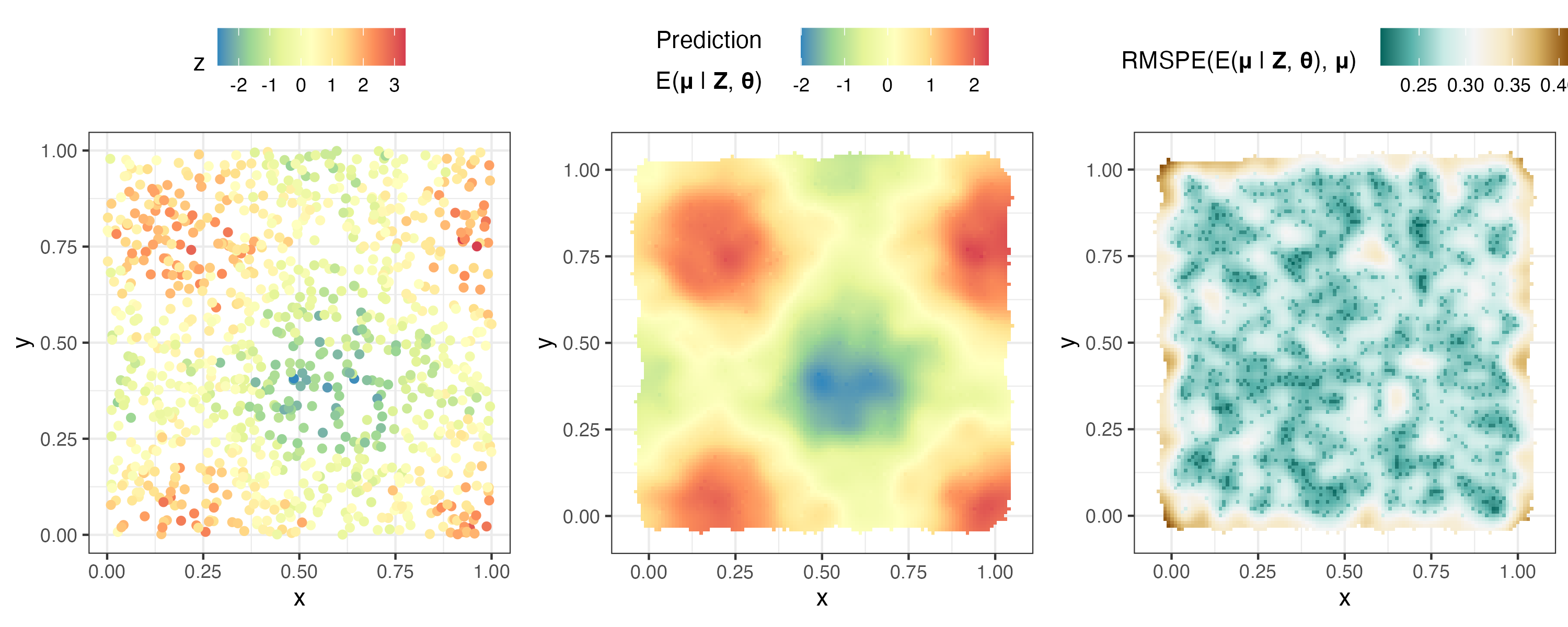
Hier analysieren wir simulierte Poisson-Daten. Wir bezeichnen ein Poisson-Datenmodell mit einer mittleren Antwort, die mithilfe der Quadratwurzel-Link-Funktion modelliert wird, indem wir in FRK() response = "poisson" und link = "sqrt" festlegen. Weitere in FRK verfügbare nicht-Gaußsche Antwortverteilungen sind die Binomial-, die Negativ-Binomial-, die Gamma- und die inverse Gaußsche Verteilung.
# # Simulate Poisson data using the previous example's data to construct a mean
zdf $ z <- rpois( m , lambda = zdf $ z ^ 2 )
# # Run FRK
S <- FRK( f = z ~ 1 , list ( zdf ),
response = " poisson " , # Poisson data model
link = " sqrt " ) # square-root link function
pred <- predict( S )
# # Plotting
plotlist <- plot( S , pred $ newdata )
ggarrange( plotlist $ z , plotlist $ p_mu , plotlist $ interval90_mu ,
nrow = 1 , legend = " top " )
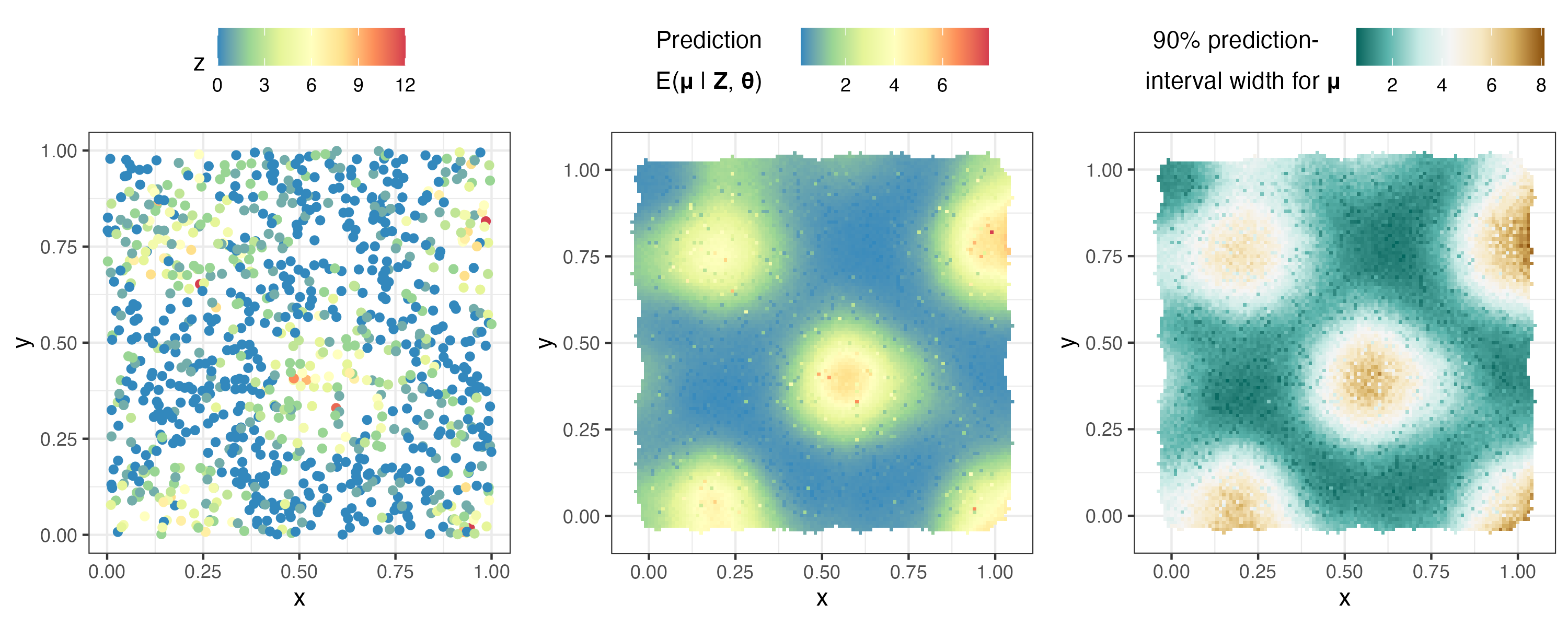
Wir analysieren nun räumlich-zeitliche Daten mithilfe des NOAA-Datensatzes.
# # Setup
library( " spacetime " )
data( " NOAA_df_1990 " )
Tmax <- subset( NOAA_df_1990 , month %in% 7 & year == 1993 )
Tmax <- within( Tmax , { time = as.Date(paste( year , month , day , sep = " - " ))})
STObj <- stConstruct( x = Tmax , space = c( " lon " , " lat " ), time = " time " , interval = TRUE )
# # BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs( manifold = STplane(),
cellsize = c( 1 , 1 , 1 ),
data = STObj , tunit = " days " )
BAUs $ fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
# # Basis functions
G <- auto_basis( manifold = STplane(), data = STObj , nres = 2 , tunit = " days " )
# # Run FRK
STObj $ std <- 2 # fix the measurement error variance
S <- FRK( f = z ~ 1 + lat , data = list ( STObj ),
basis = G , BAUs = BAUs , est_error = FALSE , method = " TMB " )
pred <- predict( S , percentiles = NULL )
# # Plotting: include only some times via the argument subset_time
plotlist <- plot( S , pred $ newdata , subset_time = c( 1 , 7 , 13 , 19 , 25 , 31 ))
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )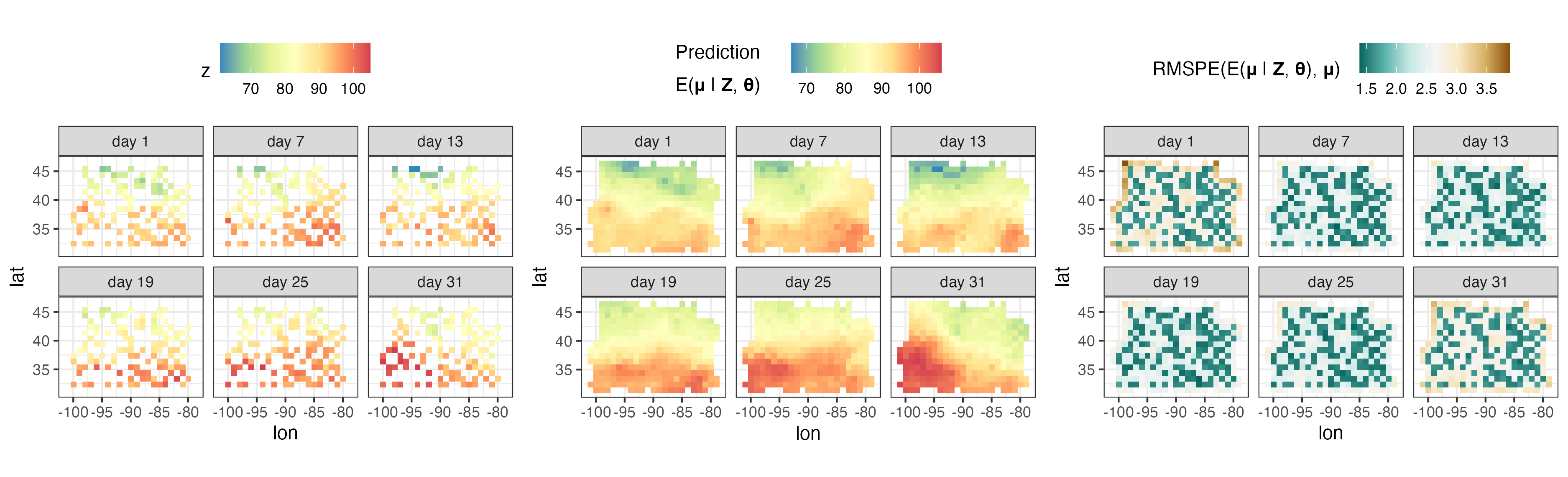
Das Paket FRK wird derzeit verwendet, um räumlich-zeitliche Animationen von Feldern zu erzeugen, die durch Satellitendaten beobachtet werden. Hier zeigen wir eine tägliche CO2-Vorhersage anhand von Daten des NASA OCO-2 zwischen September 2014 und Juni 2016.
Vielen Dank an Michael Bertolacci für die Gestaltung des FRK-Hex-Logos!