smard power forecasting
1.0.0
Dieses Repository dient der Prognose des deutschen Stromverbrauchs.
Basierend und inspiriert von:
Datenquelle: SMARD
Legen Sie alle heruntergeladenen Dateien ab in:
/example/dataset # there is already used dataset included if you pull, but you could update
Sehen Sie sich die Datei „forecast.Rmd“ an, um zu sehen, wie Sie diesen Code auf einer aktualisierten Version von SMARD-Data ausführen können.
Verwendete Bibliotheken:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
Versuchen Sie zunächst, im Ordner „example/“ zu arbeiten.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
Folgende Funktionen wurden aus dem Datensatz und der Feiertags-API generiert:
| Index | Spaltenname | Beschreibung |
|---|---|---|
| 1 | DatumVon | Zur Validierung von DateIndex (ähnlich, aber roh) |
| 2 | Stromverbrauch | Stromverbrauch in MW |
| 3 | DateIndex | Zeitstempel (jjjj-mm-tt hh:mm:ss) |
| 4 | Wochentag | Mo, Di, Mi, Do, Fr, Sa, So (Wochentage auf Deutsch) |
| 5 | Datum | Datum (JJJJ-MM-TT) |
| 6 | Jahr | Jahr jjjj |
| 7 | Woche | Wochennummer 0-53 |
| 8 | Stunde | Stundenzahl 0-24 |
| 9 | Monat | Monatsnummer 1-12 |
| 10 | lokalerName | Name eines Feiertags für den Zeitstempel |
| 11 | Werktag | 1/0 Wenn Werktag, dann 1 |
| 12 | Mo | 1/0 Wenn Montag, dann 1 |
| 13 | Di | 1/0 Wenn Dienstag, dann 1 |
| 14 | Mi | 1/0 Wenn Mittwoch, dann 1 |
| 15 | Tun | 1/0 Wenn Donnerstag, dann 1 |
| 16 | Fr | 1/0 Wenn Freitag, dann 1 |
| 17 | Sa | 1/0 Wenn Samstag, dann 1 |
| 18 | Also | 1/0 Wenn Sonntag, dann 1 (nicht erforderlich, wenn Mo.-Sa. verwendet wird) |
| 19 | Urlaub | 1/0 Wenn es ein Feiertag ist, dann 1 |
| 20 | ArbeitstagFeiertagWochenende | Wenn es ein Feiertag, ein Wochenende oder ein Werktag ist (bei Grundstücken ist dies Char.) |
| 21 | HolidayAndWorkDay | 1/0 Wenn der Feiertag auf einen Werktag fällt, dann 1 |
| 22 | LastDayWasNotWorkDay | 1/0 Wenn der letzte Tag kein Arbeitstag war, dann 1 |
| 23 | LastDayWasNotWorkDayAndNowWorkDay | 1/0 Wenn der letzte Tag kein Arbeitstag war und es jetzt ein Arbeitstag ist, dann 1 |
| 24 | NextDayIsNotWorkDayAndNowWorkDay | 1/0 Wenn der nächste Tag kein Arbeitstag ist und jetzt ein Arbeitstag, dann 1 |
| 25 | LastDayWasHolidayAndNotWeekend | 1/0 Wenn der letzte Tag ein Feiertag und kein Wochenende war, dann 1 |
| 26 | NextDayIsHolidayAndNotWeekend | 1/0 Wenn der nächste Tag ein Feiertag und kein Wochenende ist, dann 1 |
| 27 | Feiertagsname | ähnlich wie localName (Name des Feiertags) |
| 28 | Jahresende | 1/0 Wenn es das Ende des Jahres ist (Woche 52 oder 53) |
| 29 | Erste Woche des Jahres | 1/0 Wenn es Anfang des Jahres ist (Woche 1) |
| 30 | Urlaub verlängert | 1/0 verzögerter Feiertag (6 Stunden bis zum nächsten Tag) |
| 31 | UrlaubGeglättet | HolidayExtend + sin(2*pi(Stunde)+1)/24) |
| 32 | MeanLastWeek | Mittlerer Stromverbrauch der letzten Woche (Schicht: 24*8-25) |
| 33 | MeanLastTwoDays | Mittlerer Stromverbrauch der letzten zwei Tage (Schicht: 24*3-25) |
| 34 | MaxLastOneDay | Maximaler Stromverbrauch des letzten Tages (Schicht: 24*2-25) |
| 35 | MinLastOneDay | Min. Stromverbrauch des letzten Tages (Schicht: 24*2-25) |
In dieser Studie handelt es sich um einen Datensatz zum Stromverbrauch in Deutschland von SMARD für die Jahre 2015 – 2024.
Abbildung 1 zeigt den Rohdatensatz mit fehlenden Werten (rot), doppelten Zeitstempeln (dunkelrot) und Stromverbrauch über die Zeit (grau), stündliche Auflösung. Da jedes Jahr ein Wert fehlte und ein Duplikat vorhanden war, war es einfach, den Datensatz zu bereinigen. Insgesamt ein nahezu sauberes Set. Nach der Bereinigung des Datensatzes ergeben sich plausible Beobachtungen zum Stromverbrauch:
Es gibt einen einfachen Ansatz, die Lücken zu schließen, indem man die letzte Beobachtung macht (möglich, weil die Auflösung groß genug ist und nur wenige Werte fehlen). Für Duplikate wurde der erste Wert beibehalten.
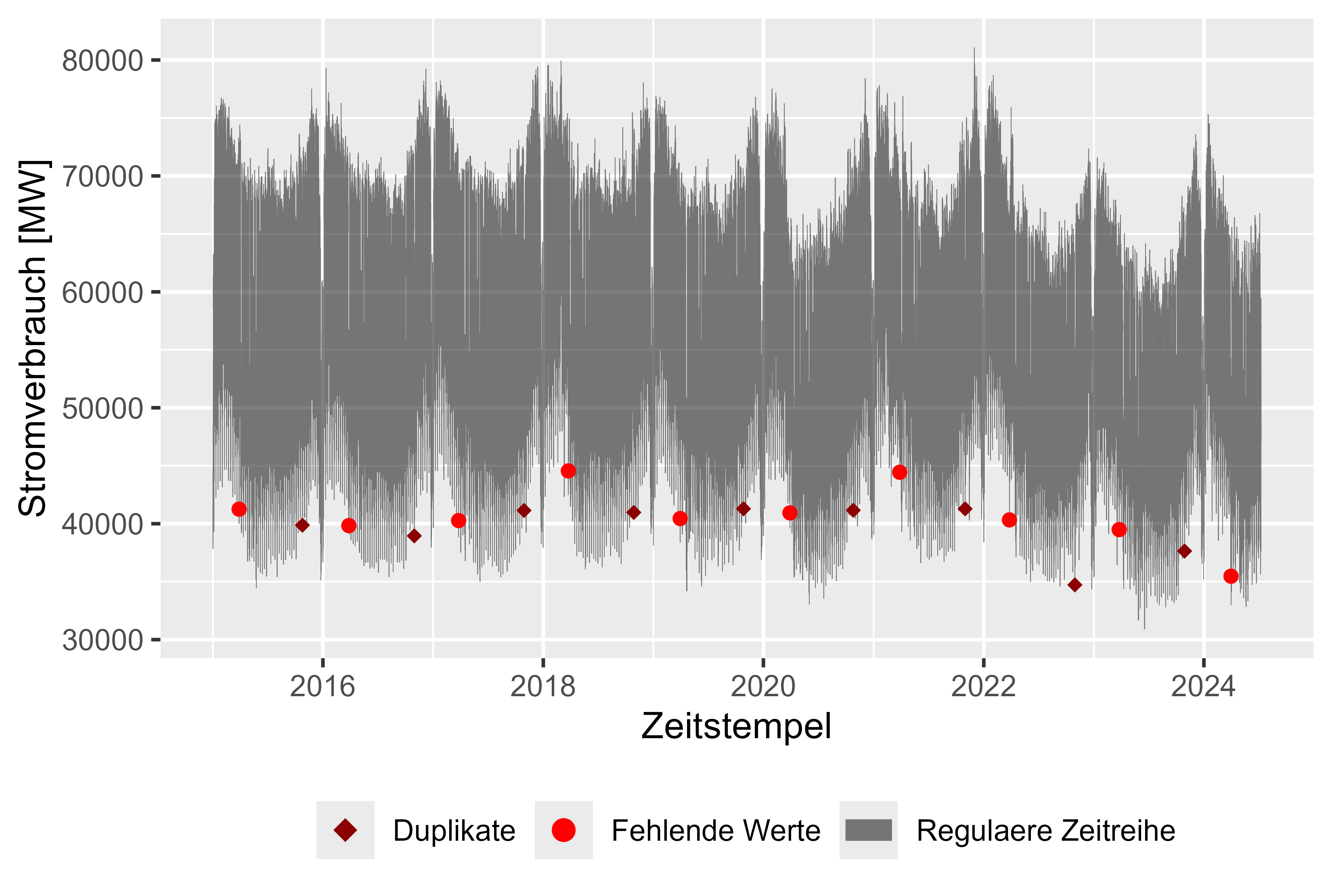Abbildung 1 Rohstromverbrauch
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
Die folgenden Abschnitte werden immer detaillierter auf die Daten eingehen. Wir beginnen hier mit der jährlichen Darstellung.
Abbildung 2 ist eine jährliche Darstellung der Jahre 2015–2024. Wir können hier feststellen, dass es zu Beginn des Jahres zu einem Anstieg des Stromverbrauchs und zum Ende des Jahres zu einem Rückgang (Weihnachten, Neujahr) kommt. Insgesamt sieht es aus wie eine Lächelnform oder eine Schleife.
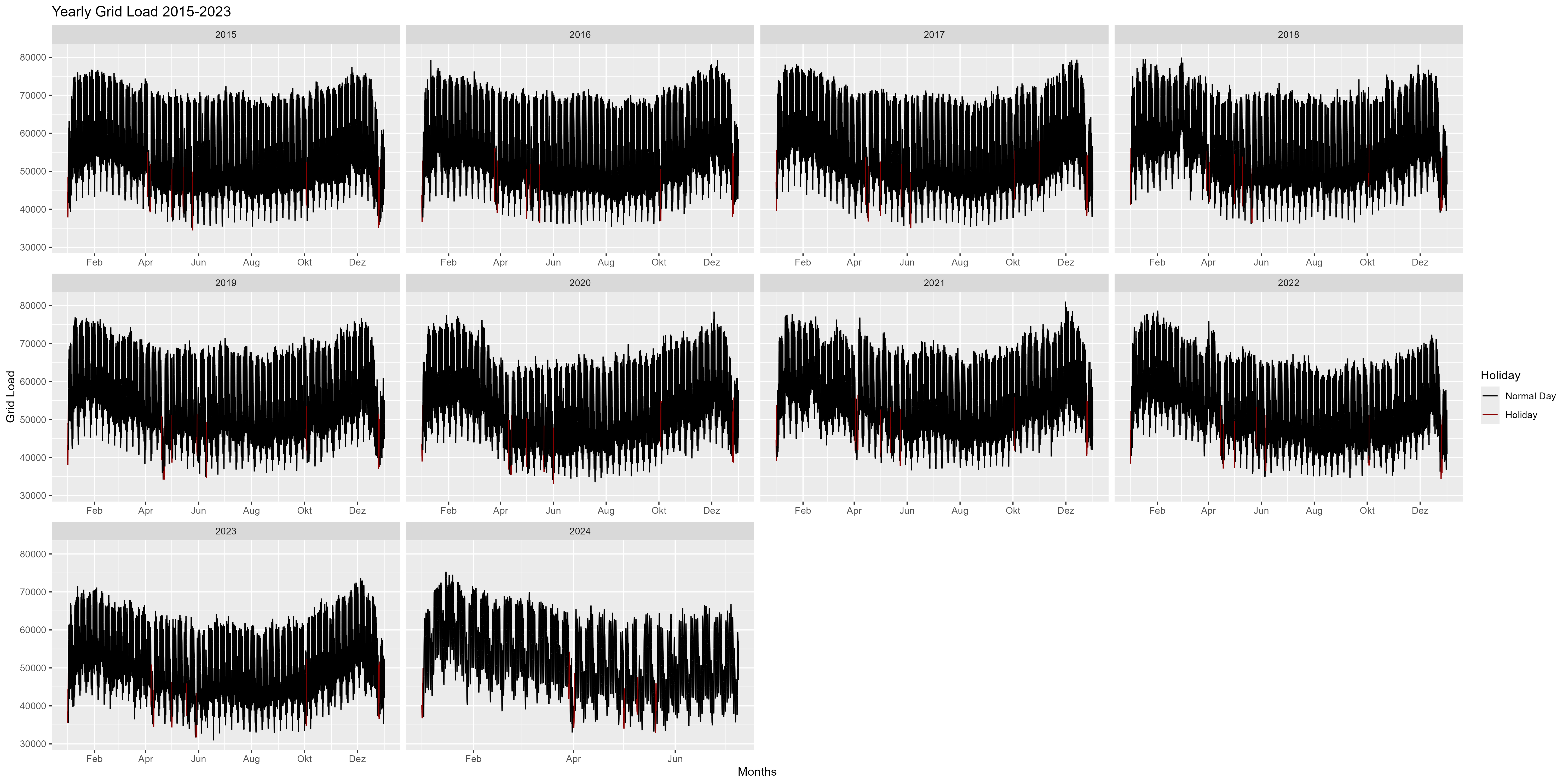Abbildung 2 Stromverbrauch, jedes Jahr als einzelne Facette
Versuchen wir, alle Jahre zusammenzufassen und in Wochen aufzuteilen. Die Boxplots in Abbildung 3 kombinieren alle Jahre. Wir können das Muster detaillierter sehen. Der Beginn und das Ende eines Jahres werden in Rot dargestellt und zeigen eine Abweichung von der regulären „Lächelnform“.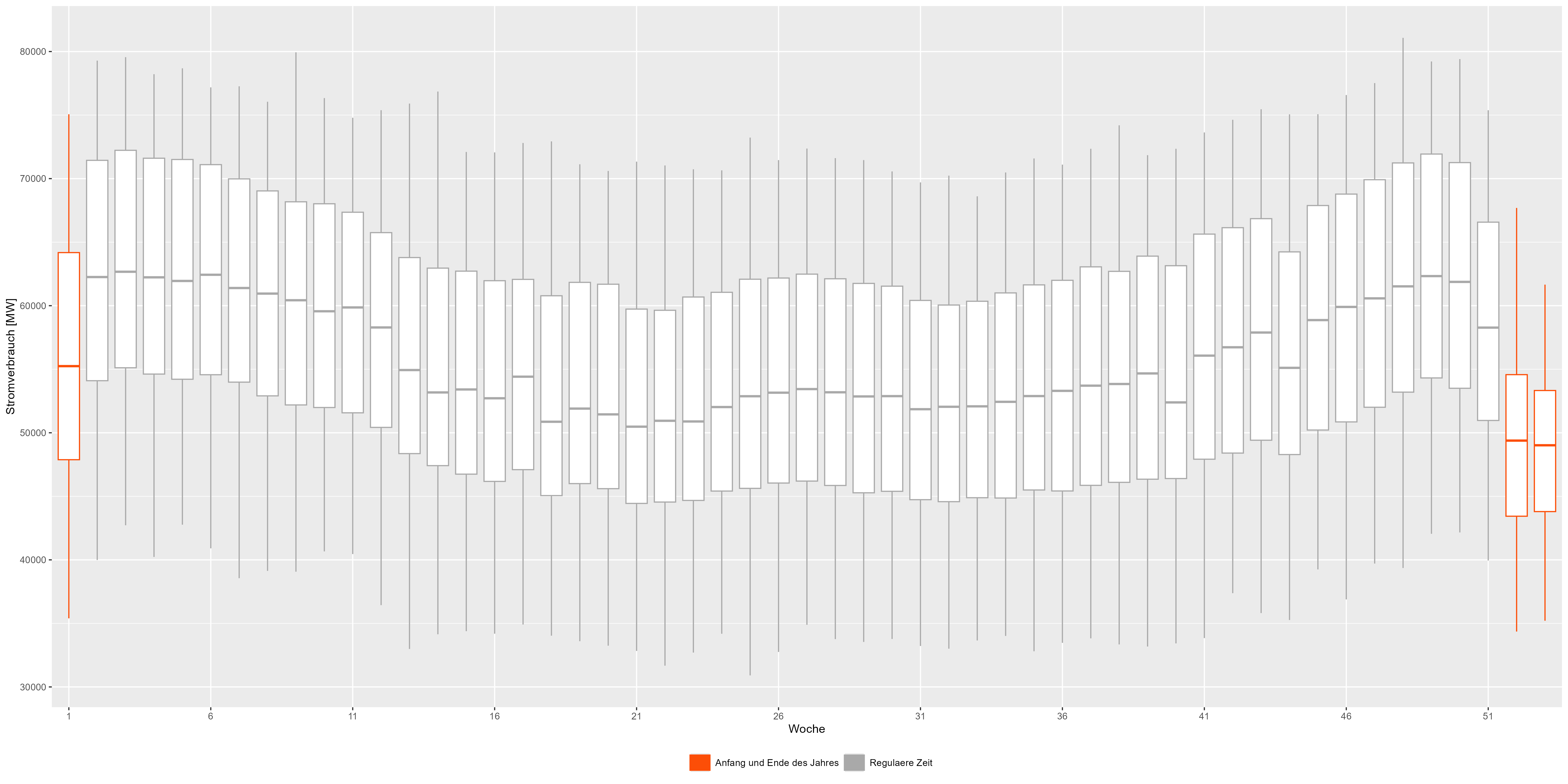
Abbildung 3 Wöchentliche aggregierte Daten zum Stromverbrauch
Gehen wir etwas detaillierter vor und blicken beispielsweise auf das Jahr 2018. Abbildung 4 ist die Monatsdarstellung des Jahres 2018. Hier können wir das Jahresende genauer beobachten. Um den 24. Dezember herum ist ein Rückgang des Stromverbrauchs zu verzeichnen. Bemerkenswert sind hier auch die Wochenenden und die Feiertage (rot). Eine Ermäßigung gilt für alle Wochenenden und alle Feiertage.
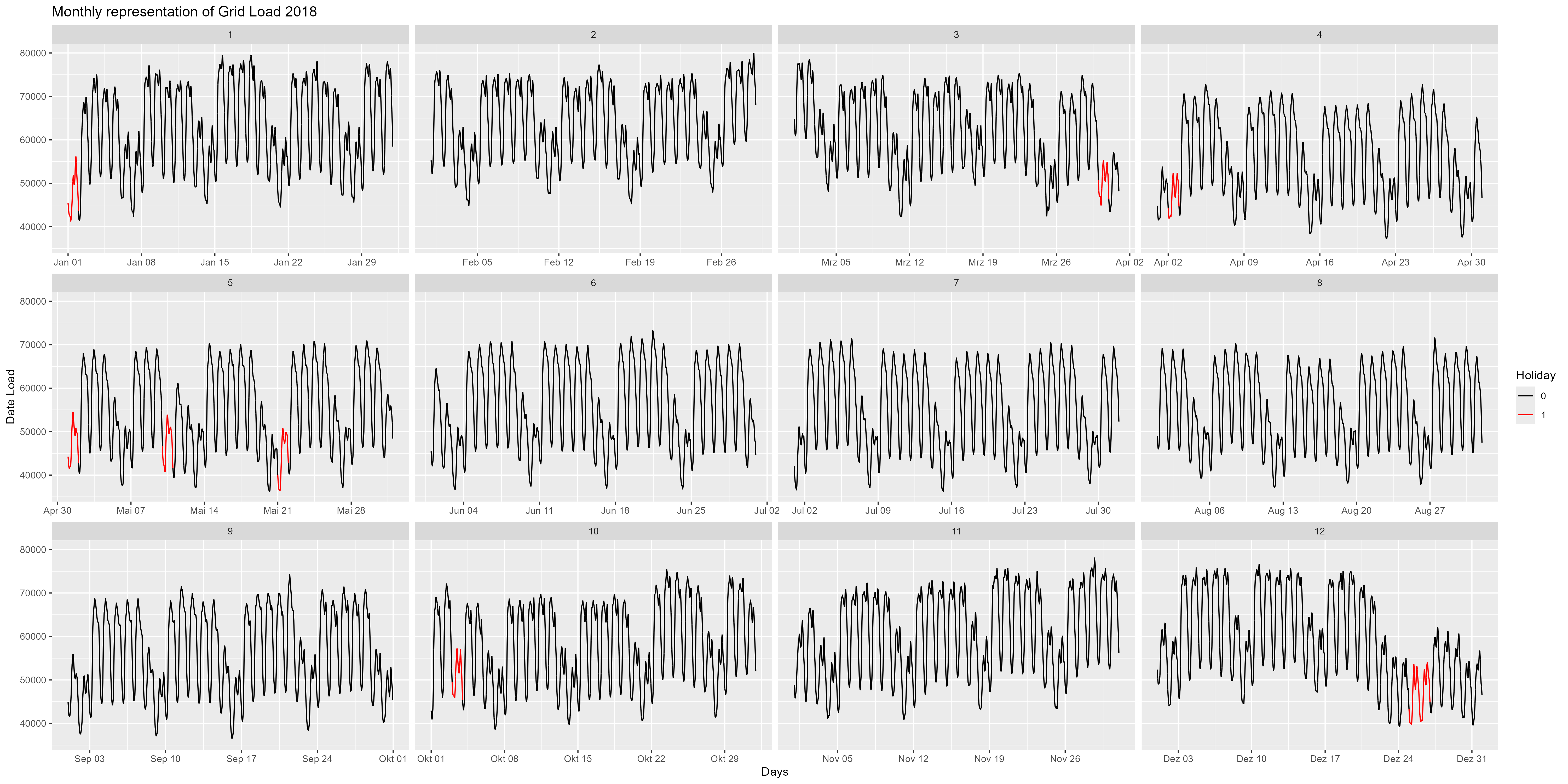Abbildung 4 Stromverbrauch, jeden Monat als einzelne Facette
Wir könnten sogar noch weiter gehen und uns die stündliche Darstellung der Daten ansehen. Abbildung 5 zeigt den aggregierten Boxplot für jede Stunde. Es gibt auch eine Verringerung der Nachtzeit (21:00–06:00 Uhr) und eine Zunahme der Tages-/Arbeitszeit (06:00–21:00 Uhr). Auch ein Muster, das in das Modell aufgenommen werden muss.
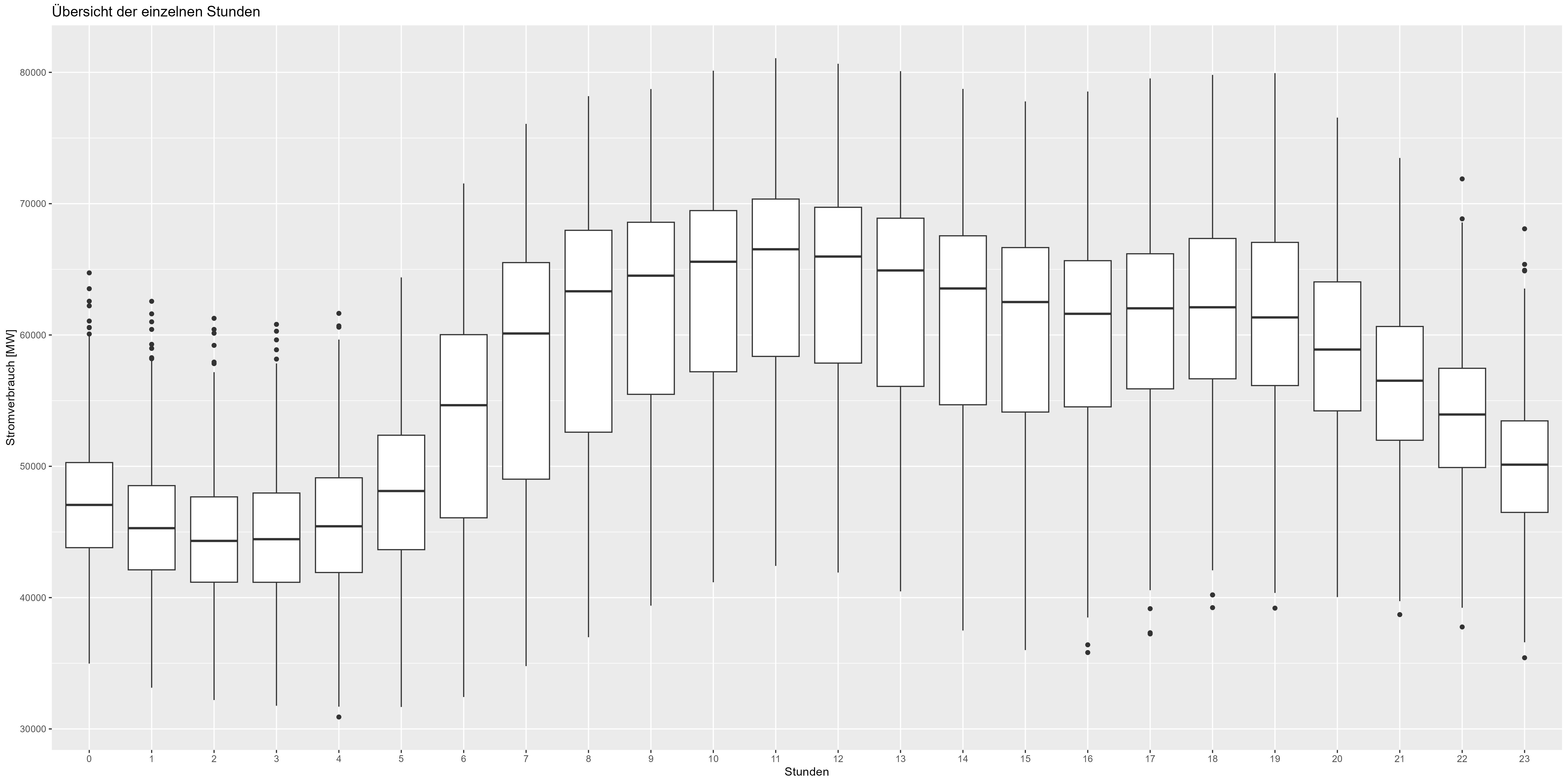Abbildung 5: Stündliche aggregierte Daten zum Stromverbrauch
Reden wir über Wochentage. Wie am Wochenende angenommen, sinkt der Stromverbrauch. „Durchschnitt“ ist der Mittelwert. Abbildung 6 zeigt alle Wochentage (aggregiert) über die Jahre. An Wochenenden gibt es einen Rückgang von ~10.000 MW.
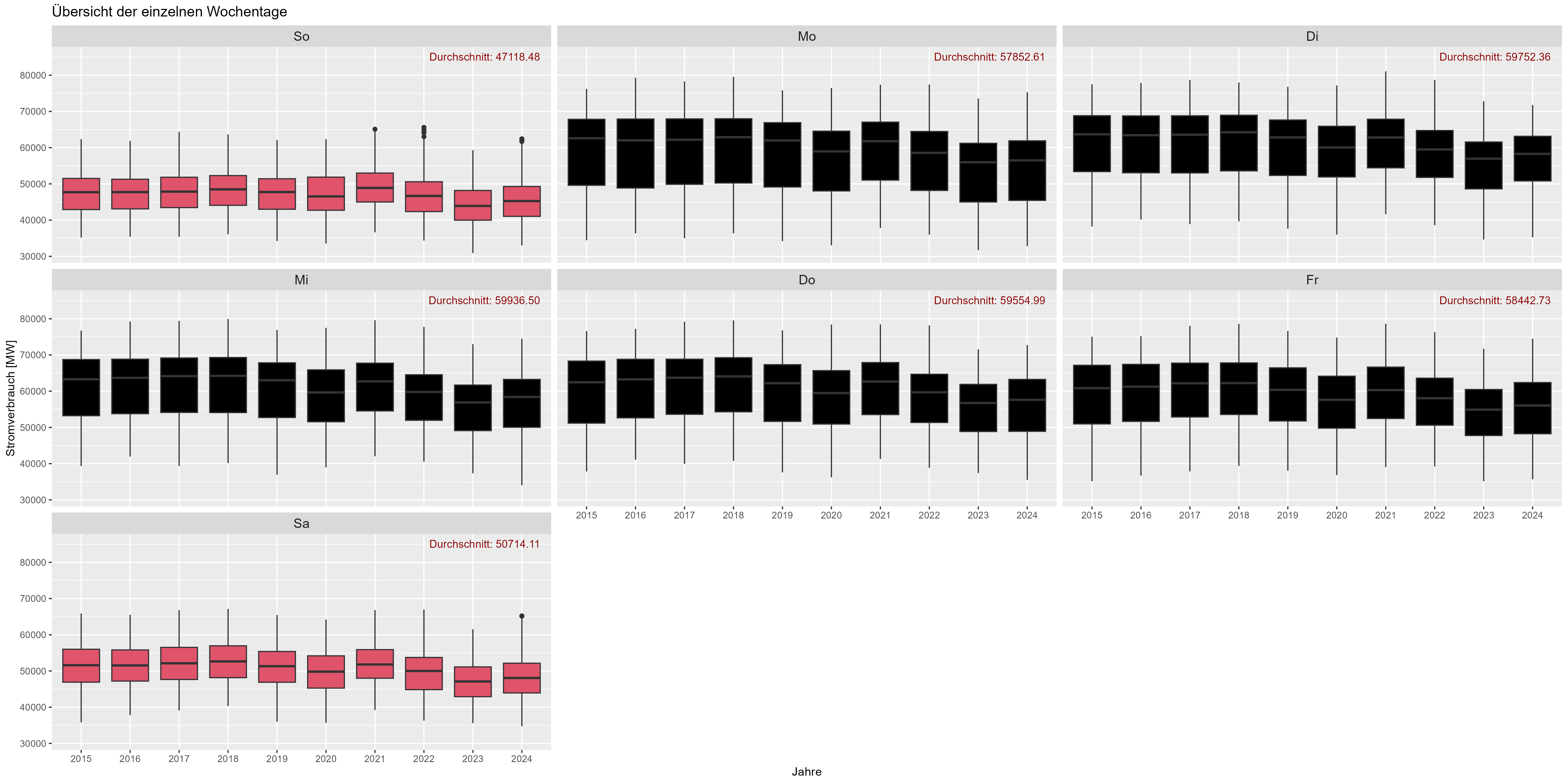Abbildung 6 Stromverbrauch „Wochentagseffekt“
Abbildung 8 zeigt den Feiertagseffekt. „Durchschnitt“ ist der mittlere Stromverbrauch über Jahre hinweg. An „Arbeitstagen“ (dunkelgrau) ist im Vergleich zu Feiertagen (rot) ein deutlicher Anstieg des Stromverbrauchs zu verzeichnen. Wir könnten hier davon ausgehen, dass Feiertage für den Stromverbraucher wie Wochenenden wirken.“
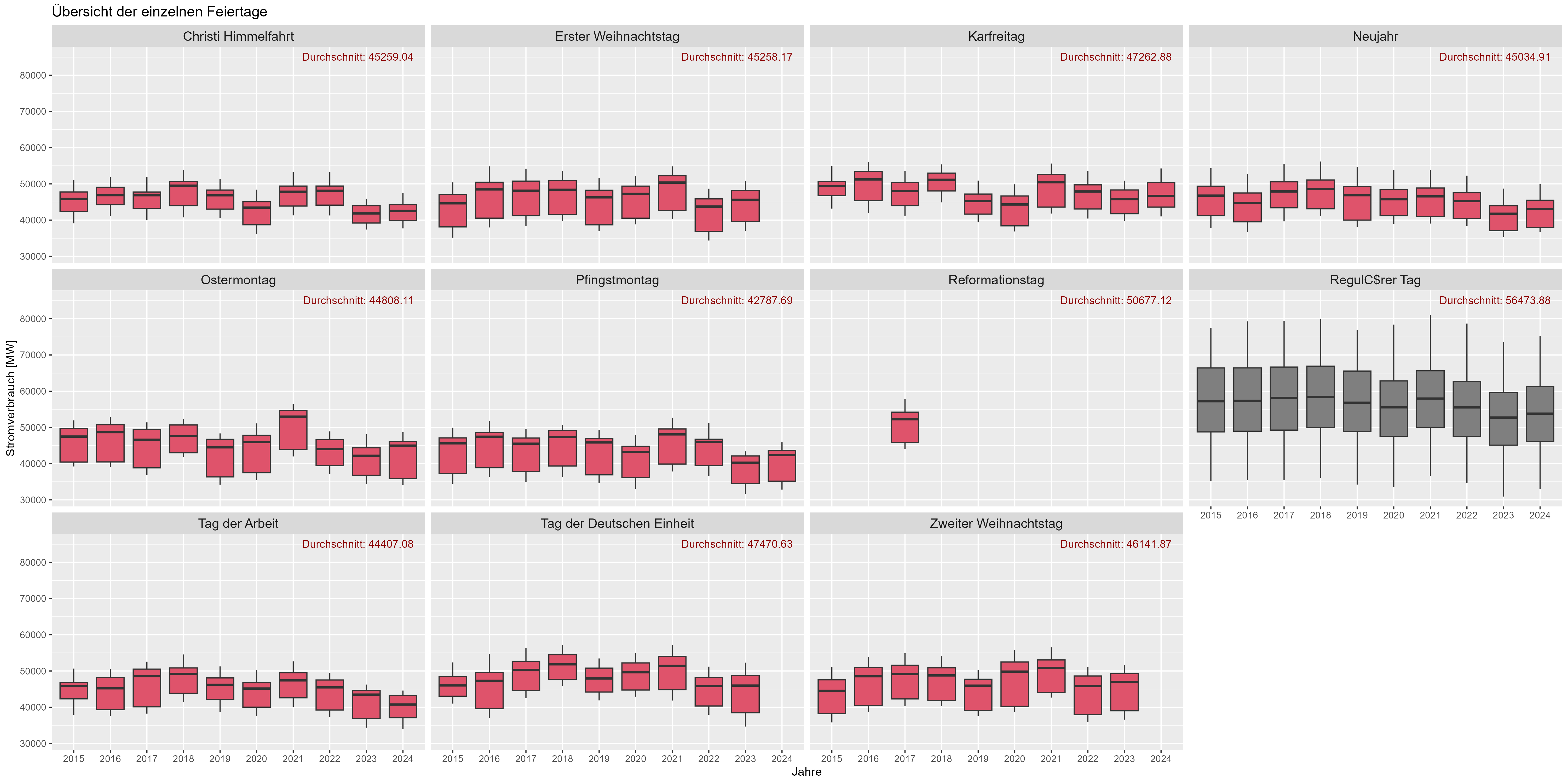Abbildung 6 Stromverbrauch „Urlaubseffekt“
Abbildung 7 zeigt unterschiedliche Verhaltensweisen für verschiedene Tage. Es gibt 4 Kategorien. „Feiertag Kein Wochenende“ bedeutet, dass es ein Feiertag ist, aber kein Wochenende. „Feiertag Wochenende“ bedeutet, dass es sich um einen Feiertag und ein Wochenende handelt. „Kein Feiertag Kein Wochenende“ bedeutet, dass es sich um einen regulären Arbeitstag handelt und „Kein Feiertag Wochenende“ bedeutet, dass es nur das Wochenende ist. Wir können ähnliche Verteilungen wie angenommen für nicht reguläre Arbeitstage beobachten.
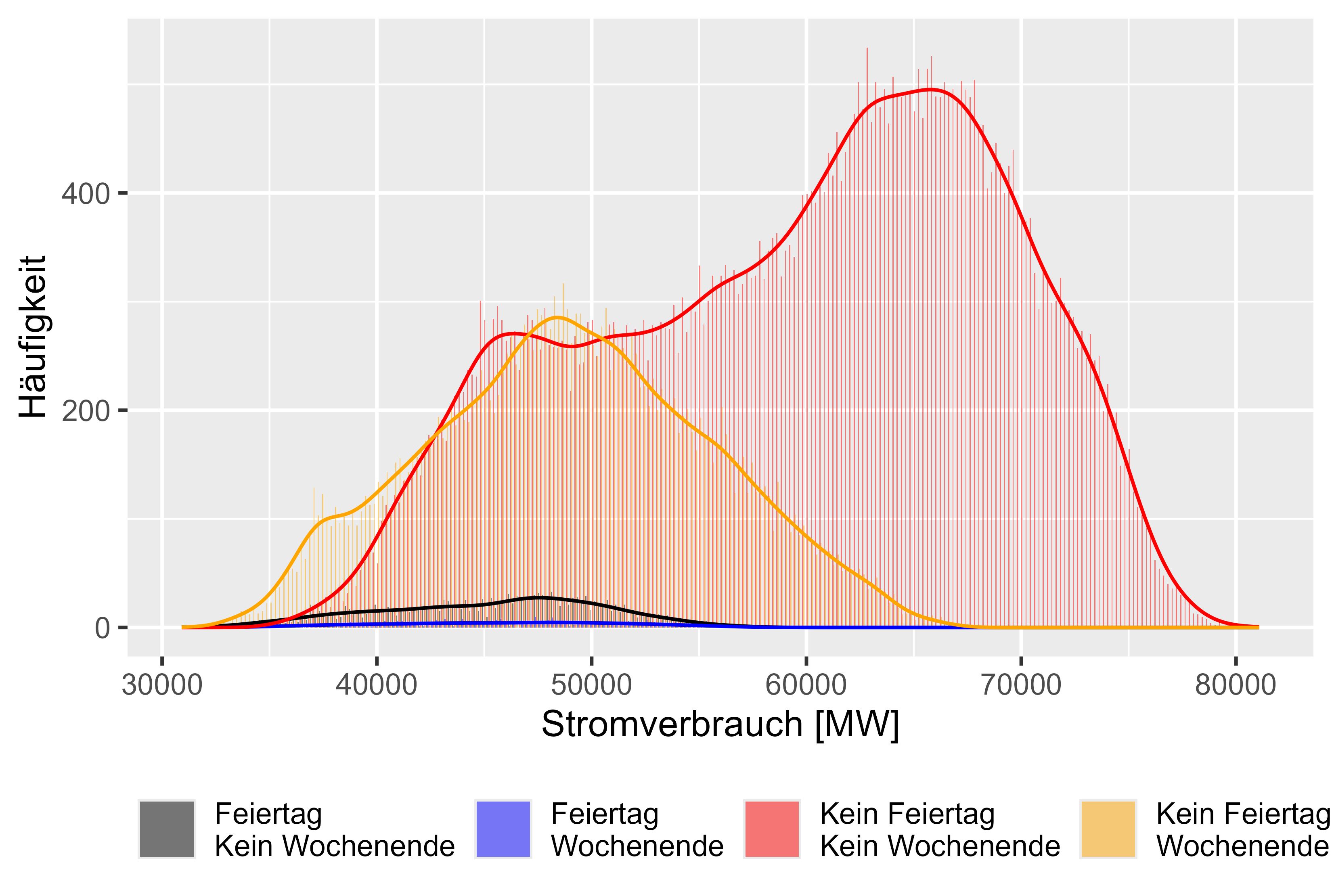Abbildung 7 Stromverbrauch „Different-Effects“ im Vergleich
Verzögerte Werte wie MeanLastTwoDays, MeanLastWeek, MaxLastOneDay und MinLastOneDay sind generierte Features.
Ähnlich wie in DOI besprochen: 10.1109/TPWRS.2011.2162082 – Kurzfristige Lastprognose basierend auf einem semiparametrischen additiven Modell
Die Abbildungen 8–11 (rot sind keine Arbeitstage) stellen diese verzögerten Werte im Vergleich zum tatsächlichen Stromverbrauch dar.
Für diese generierten Merkmale besteht eine leichte Korrelation.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| Besonderheit | Korrelation mit PowerConsum |
|---|---|
| UrlaubGeglättet | -0,556194 |
| MeanLastWeek | 0,389044 |
| MeanLastTwoDays | 0,201253 |
| MaxLastOneDay | 0,320193 |
| MinLastOneDay | 0,348583 |
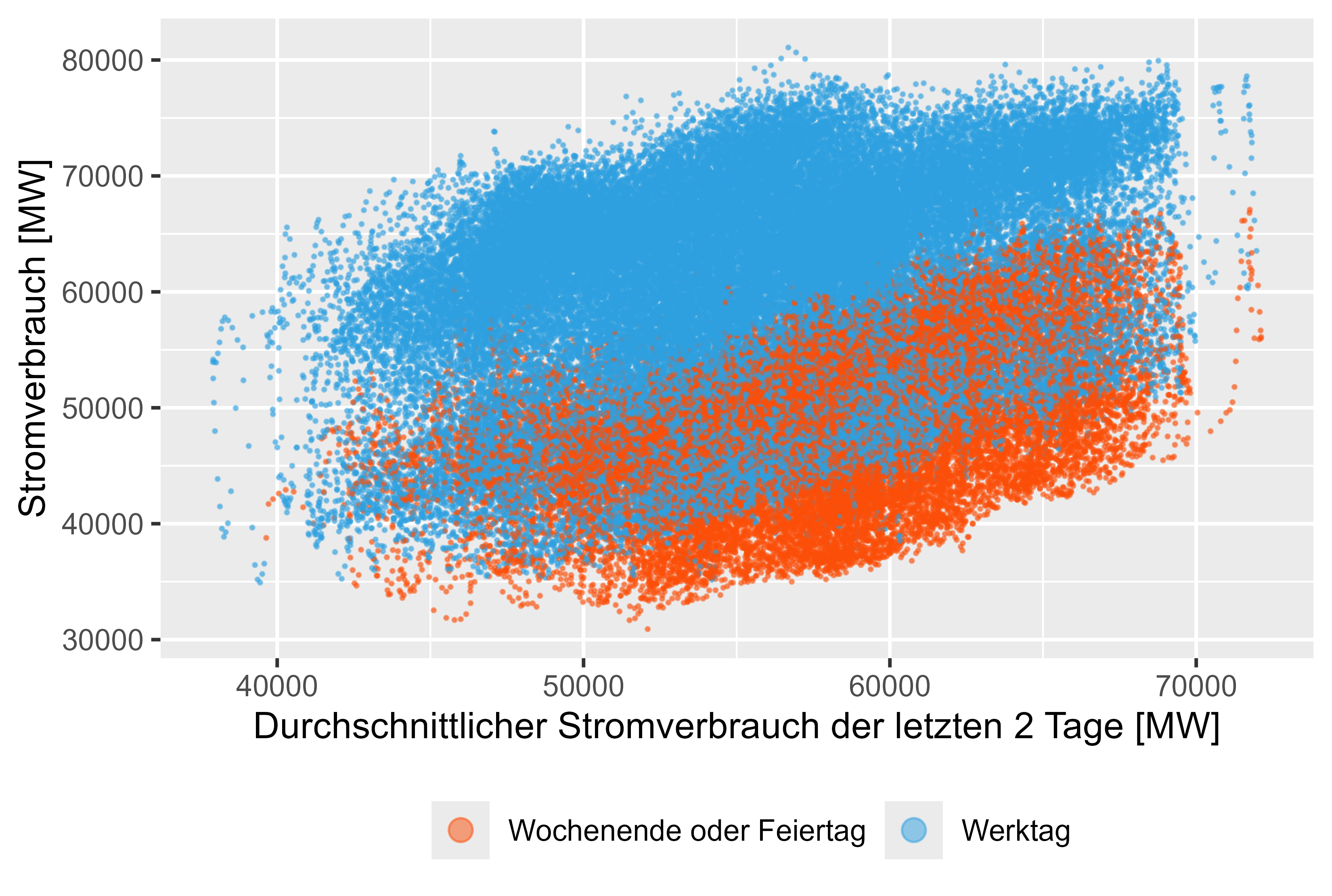Abbildung 8 Stromverbrauch – MeanLastTwoDays
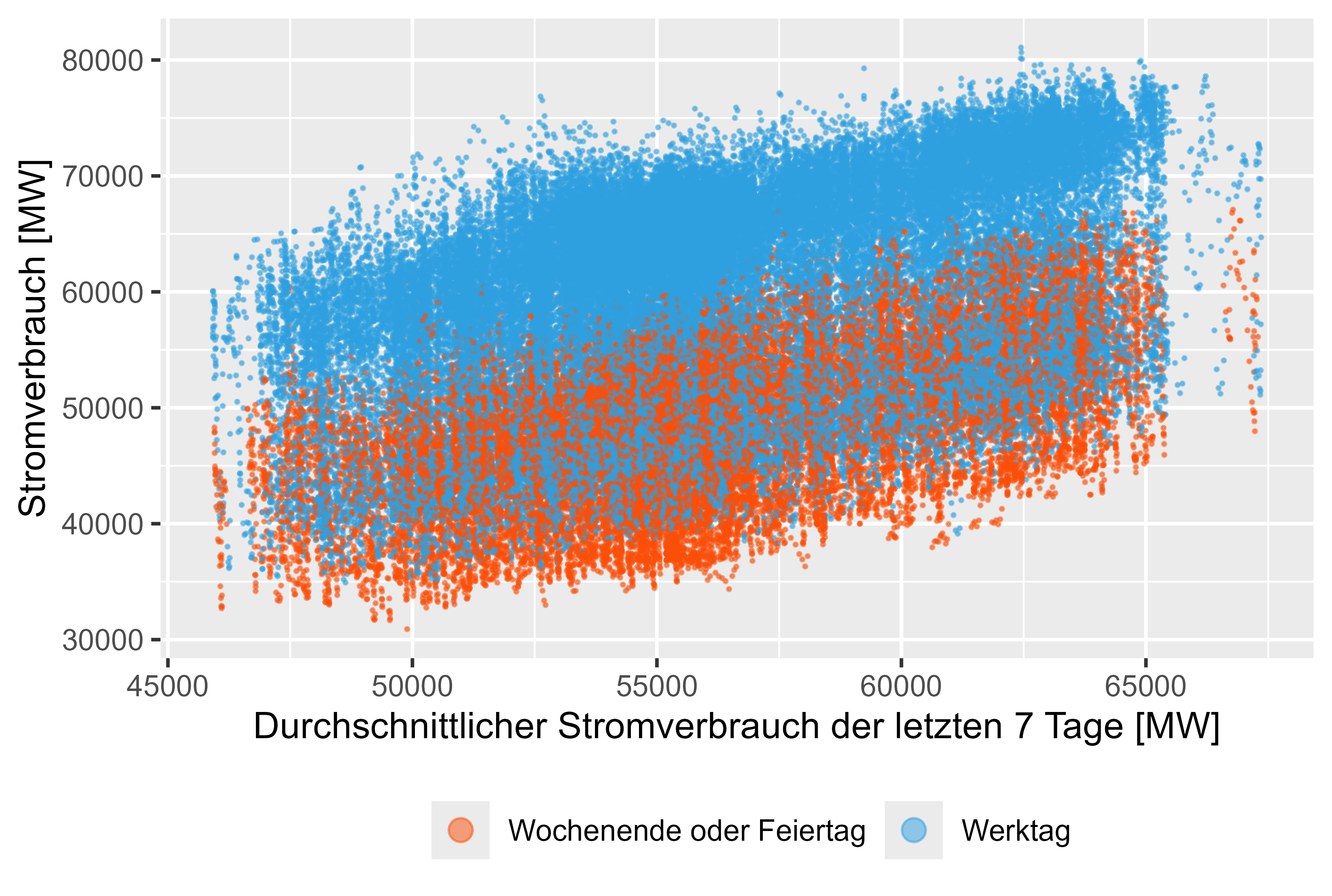Abbildung 9 Stromverbrauch – MeanLastWeek
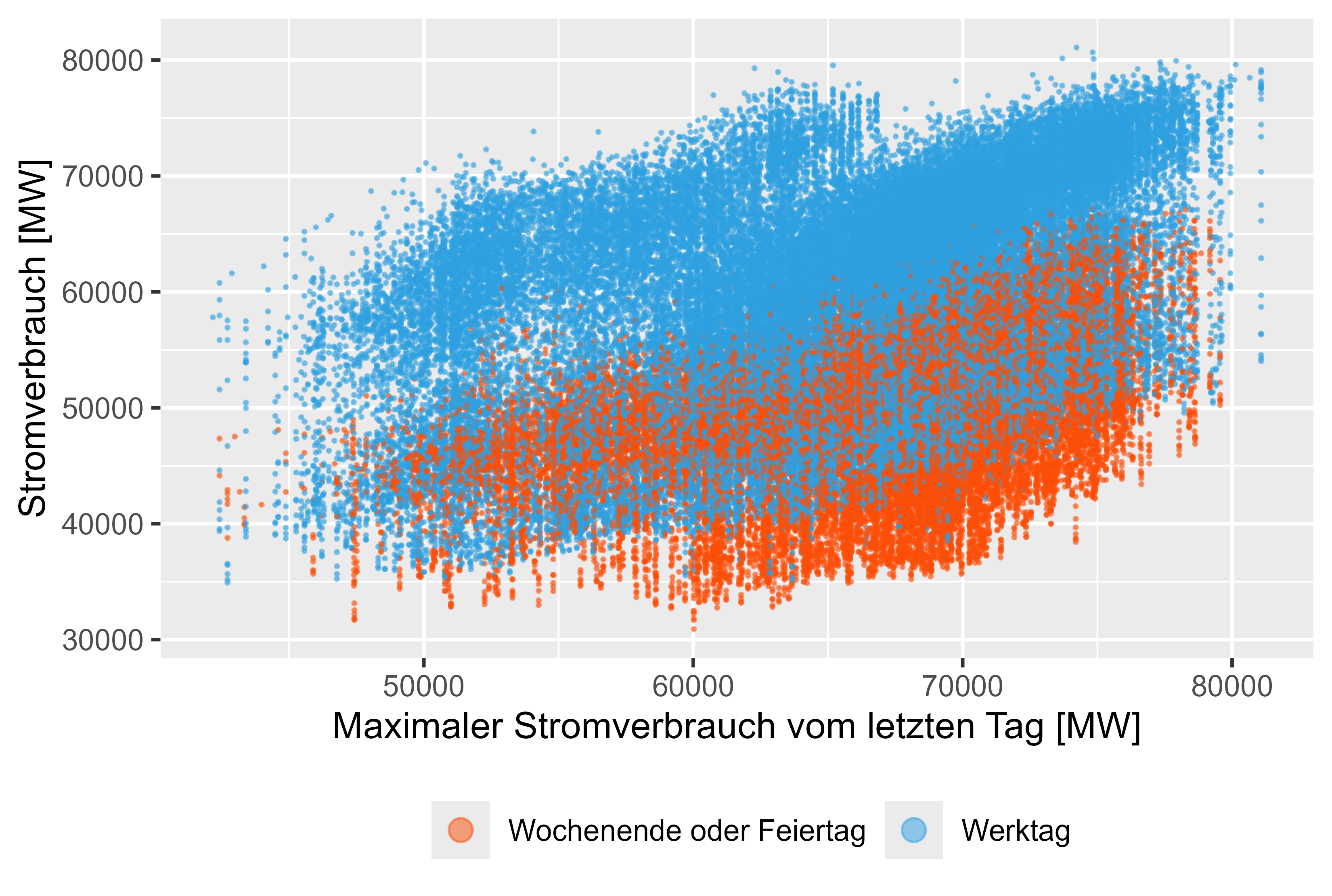Abbildung 10 Stromverbrauch – MaxLastOneDay
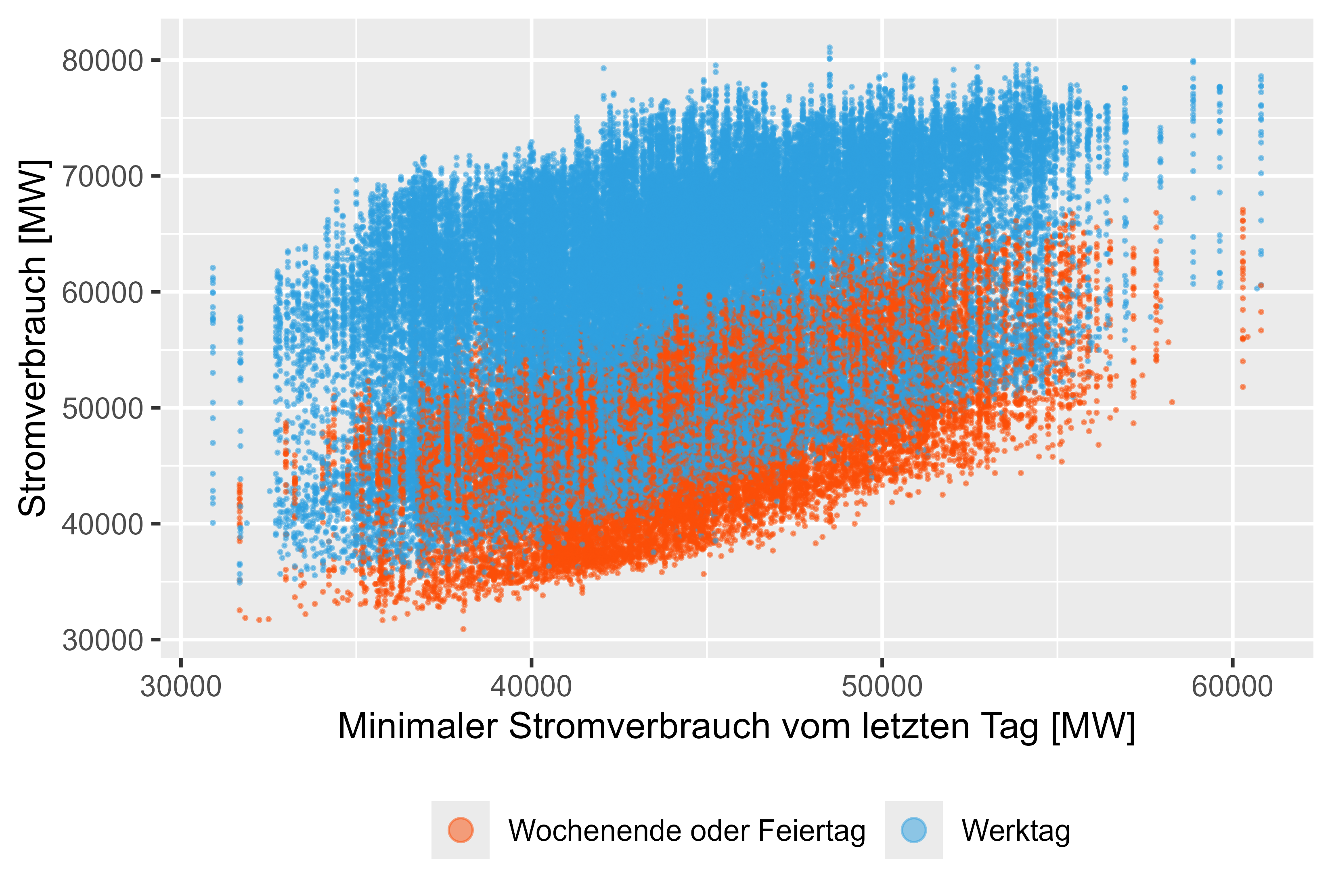Abbildung 11 Stromverbrauch – MinLastOneDay
Es gibt eine komplexe Saisonalität. Für die stündliche Auflösung gibt es eine jährliche, wöchentliche und eine tägliche Saisonalität. Was vom Modell verfolgt werden muss. Die Lösung hier ist, wie in „Prognose: Prinzipien und Praxis“, Kapitel 12.1 „Komplexe Saisonalität“, besprochen, Fourier-Terme zu verwenden, um die komplexe Saisonalität über cos() und sin() darzustellen und zusammenzusetzen.
Wir können einen kleinen Blick auf das ACF- und PACF-Diagramm werfen, es gibt nur wenige signifikante Spitzen, aber es ist nur die Darstellung von 96 verzögerten Werten. Wenn wir die etwa 9.000 verzögerten Beobachtungen über ein Jahr hinweg betrachten, gäbe es eine komplexe Saisonalität. Aus diesem Grund ist es einfacher, den Fourier-Term zu verwenden. Es hat auch nicht gut funktioniert, nur PDQ und PDQ-Komponenten zu finden
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
selbst. Auch die Trainingszeit erhöht sich ohne die Fourier-Terme dramatisch.
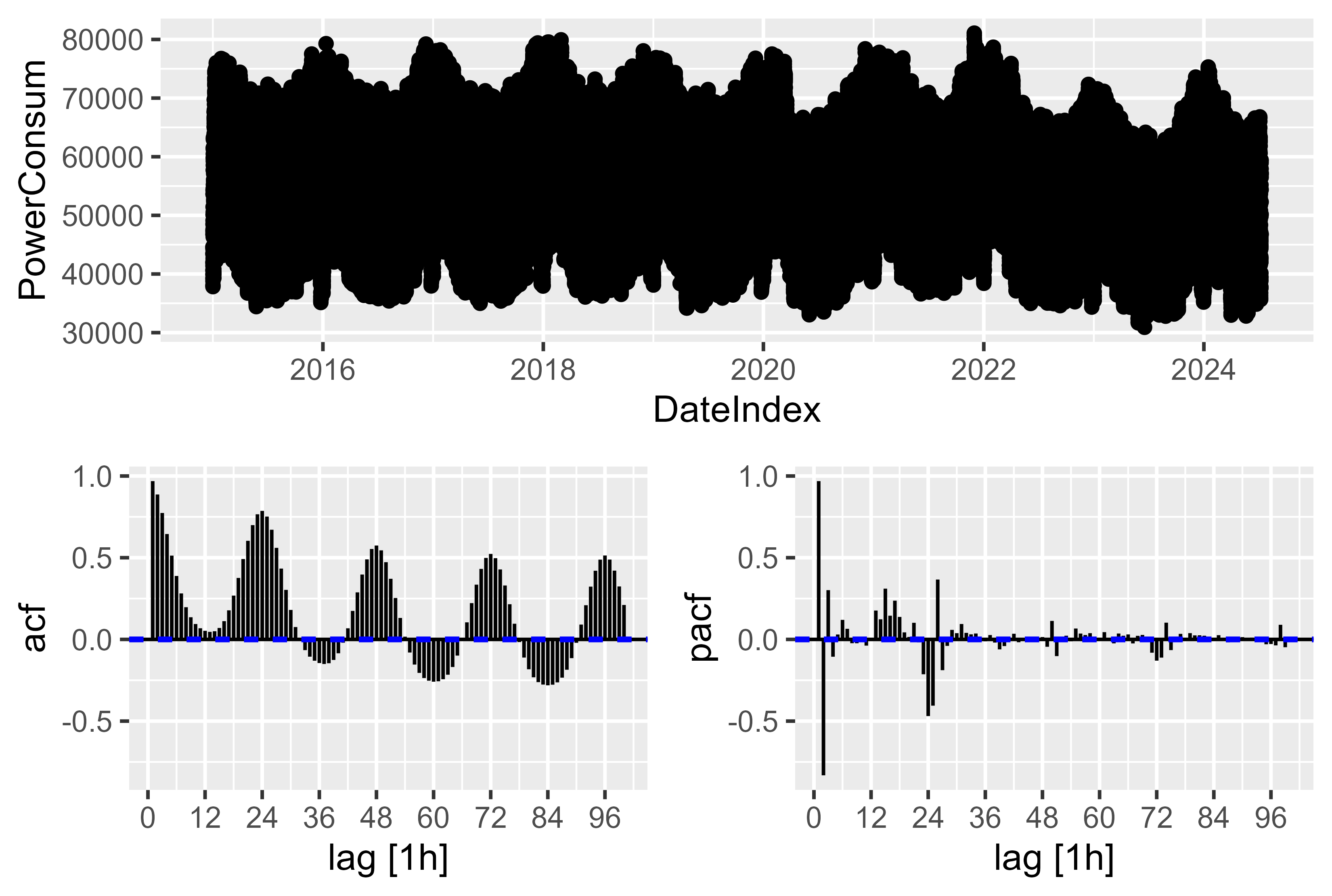Abbildung 12 Stromverbrauch – ACF PACF Diagramm des Rohstromverbrauchs
Die besten in dieser Arbeit gefundenen Funktionskombinationen sind:
Zum Vergleich der Modelle verwenden wir die Metriken MAE und MAPE. SMARD ist das Modell der Bundesnetzagentur auf der SMARD-Seite. Das Prophet-Modell wurde ebenfalls ausprobiert und funktionierte solide, aber nicht gut genug.
Die von SMARD prognostizierten Werte erreichten einen MAPE von 3,6 %. <- NICHT IN DIESER STUDIE.
Trainingsdaten:
Das beste bisher gefundene Modell war LHM + DHR (linear-harmonisches Modell + dynamische-harmonische Regression)
Die Idee besteht darin, ein lineares Modell mit dem ARIMA-Modell zu kombinieren. Weil es für das ARIMA-Modell schwierig war, mit Dummy-Variablen für Feiertage umzugehen. Das Ensemble-Modell hat also geholfen.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
Wir konnten den Effekt und die Funktionsweise des Modells visualisieren. Abbildung 13 zeigt die Idee hinter diesem Modell. Zunächst passen wir das LHM-Modell an und berechnen die Residuen. Trainieren Sie das DHR-Modell anhand der Residuen und fassen Sie beide zusammen. Es ist sozusagen ein Spiegelbild des LHM und treibt die Werte wieder nach oben.
Für das LHM-Modell verwenden wir hier einen einfachen Ansatz, eine Sinuskurve, die sich alle 24 Stunden wiederholt und an Feiertagen oder Werktagen abnimmt oder ansteigt.
Durch die Vorhersage von LHM für neue Daten können wir die Residuen für neue Daten vorhersagen. Residuen + LHM verschieben die Werte zurück in die „richtige“ Position.
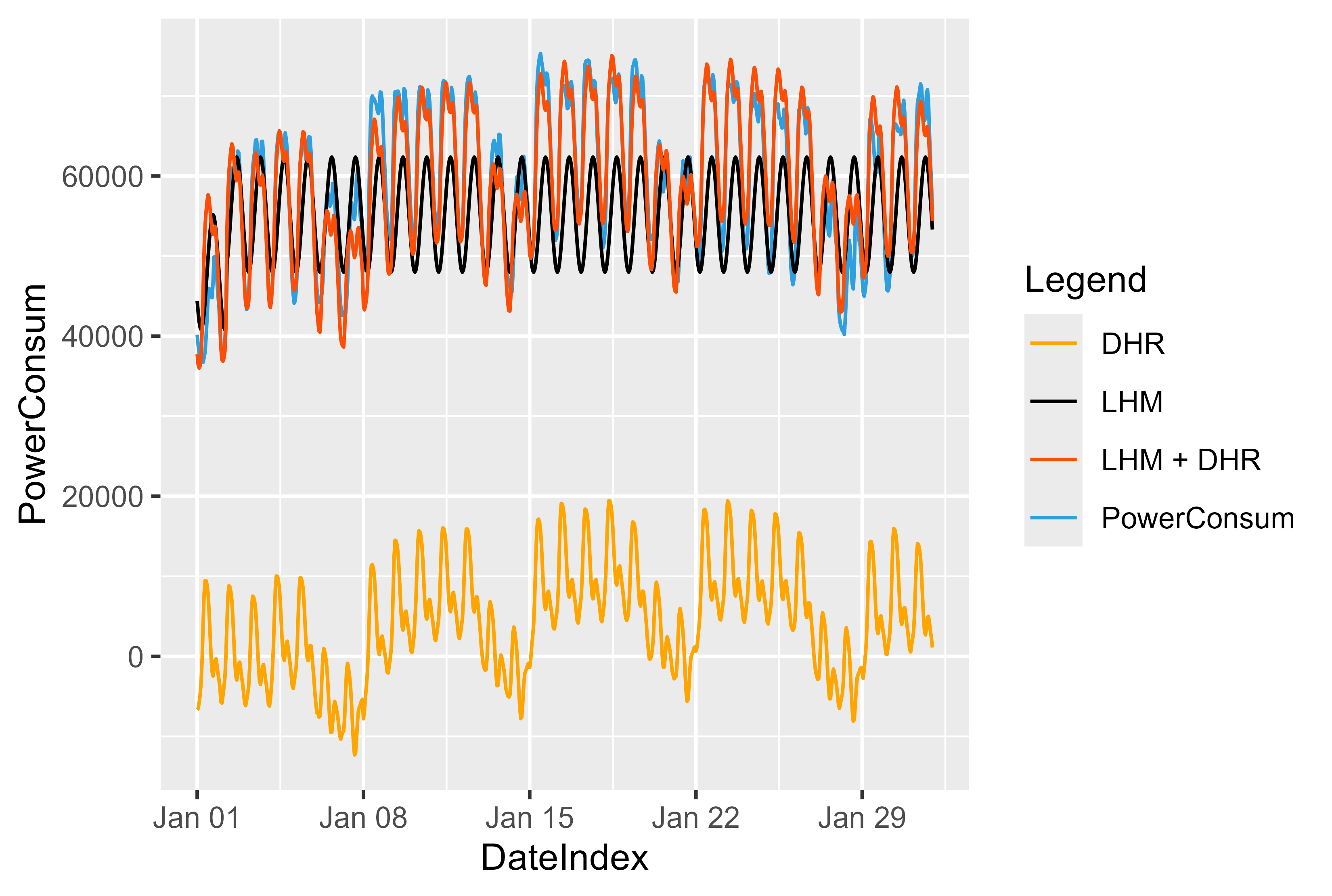Abbildung 13 Darstellung des LHM + DHR-Modells
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
Ein solider MAPE-Wert von 3,8 % für Version_5 (LHM + DHR-Modell).
Werfen wir einen genaueren Blick darauf, ob wir nur das ARIMA-Modell (arima_14) verwenden würden. Abbildung 14 zeigt die Ergebnisse für dieses Modell. Wir können die Feiertage (orange), das Wochenende (rot) und den regulären Tag (blau) sehen. Es gibt erhebliche Ausreißer für die Feiertage, obwohl es eine Dummy-Variable für das ARIMA-Modell gab, konnte diese die Feiertage nicht korrekt erfassen.
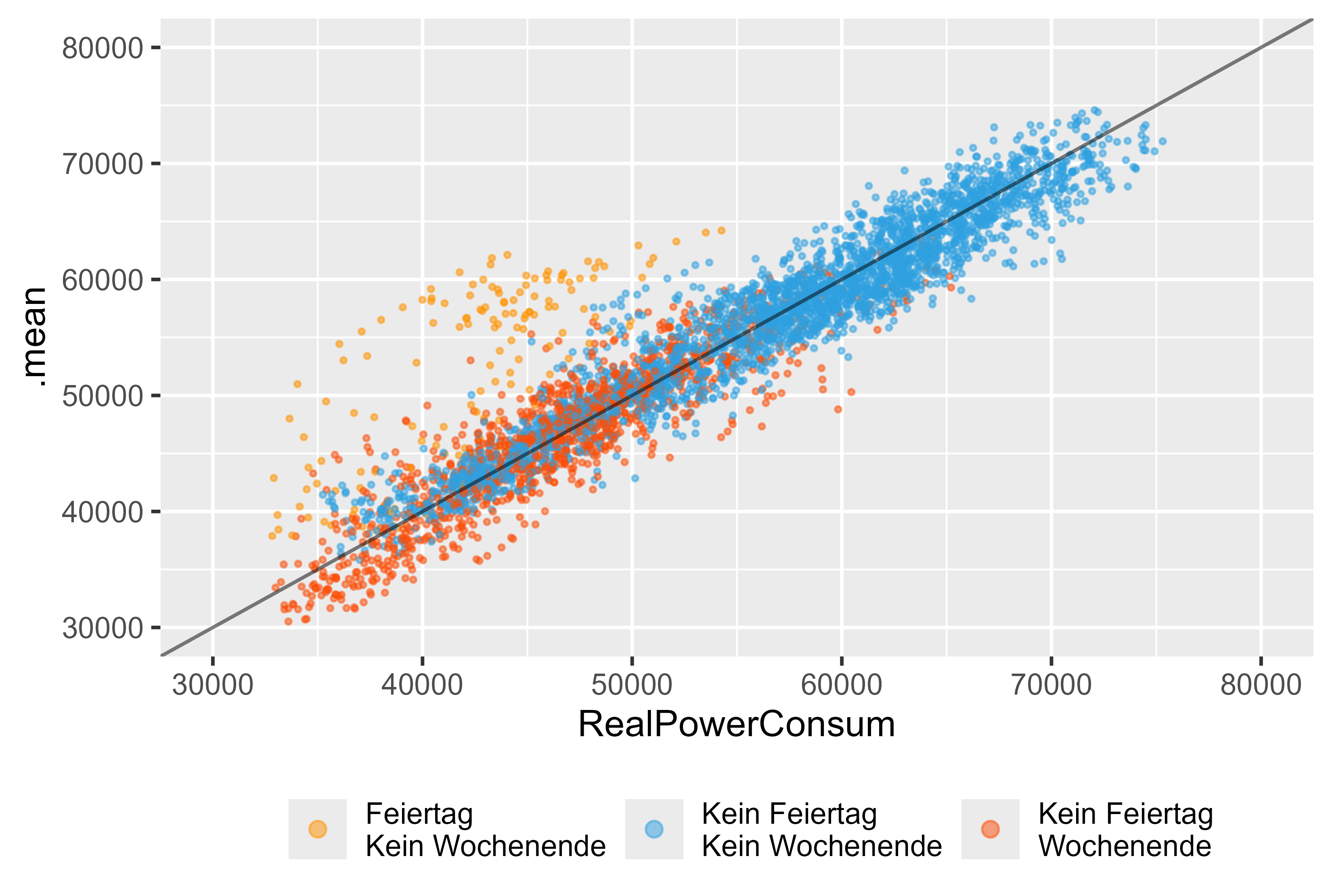Abbildung 14 Prognose vs. tatsächliche Werte ARIMA (DHR, arima_14), als einzelnes Modell
Andererseits zeigt das LHM + DHR-Modell eine bessere Leistung für die Feiertage. Abbildung 15 stellt es dar.
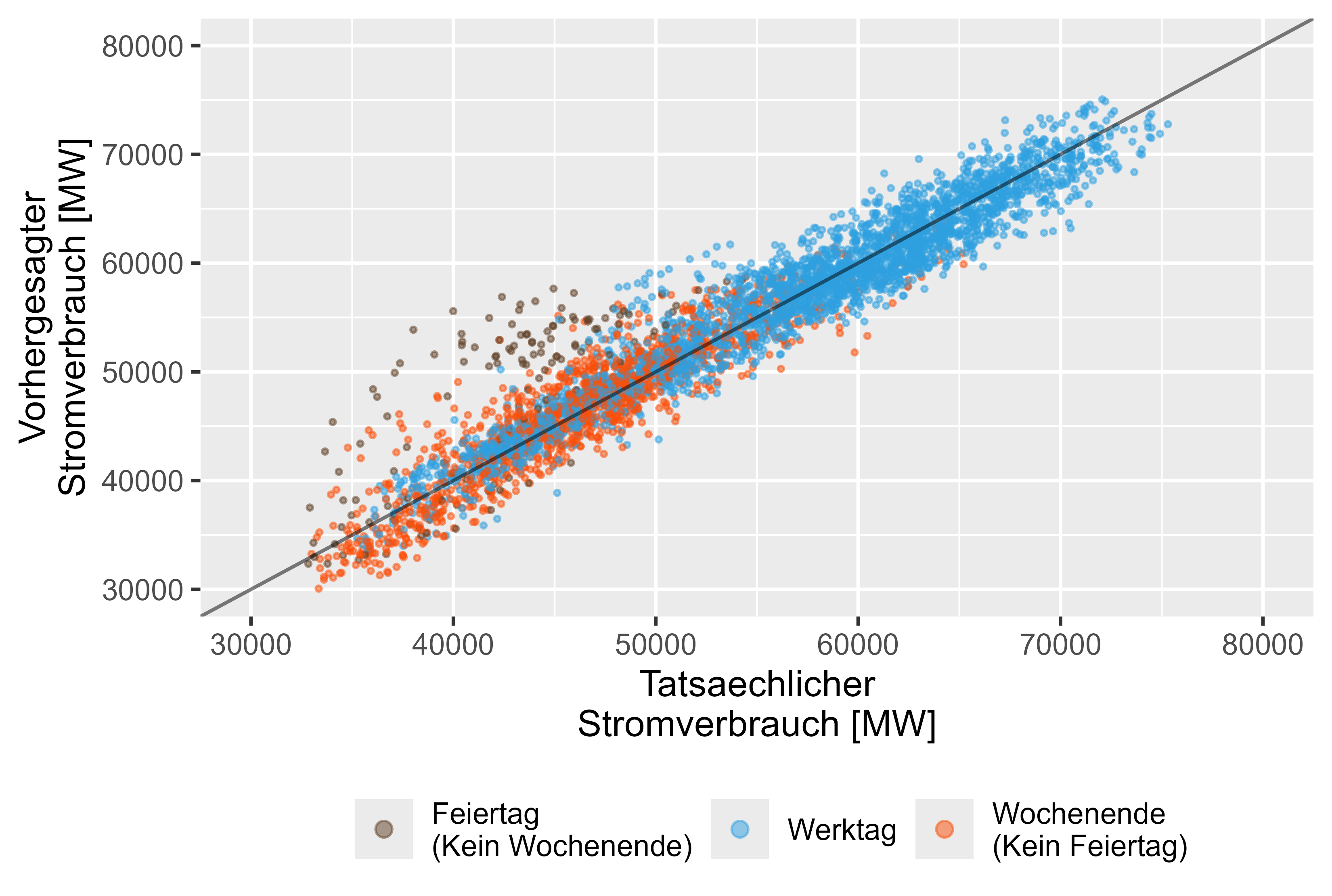Abbildung 15 Prognose vs. tatsächliche Werte LHM + DHR, Ensemblemodell
Abbildung 16 zeigt die Prognose für Januar 2024. Sie sieht vernünftig aus.
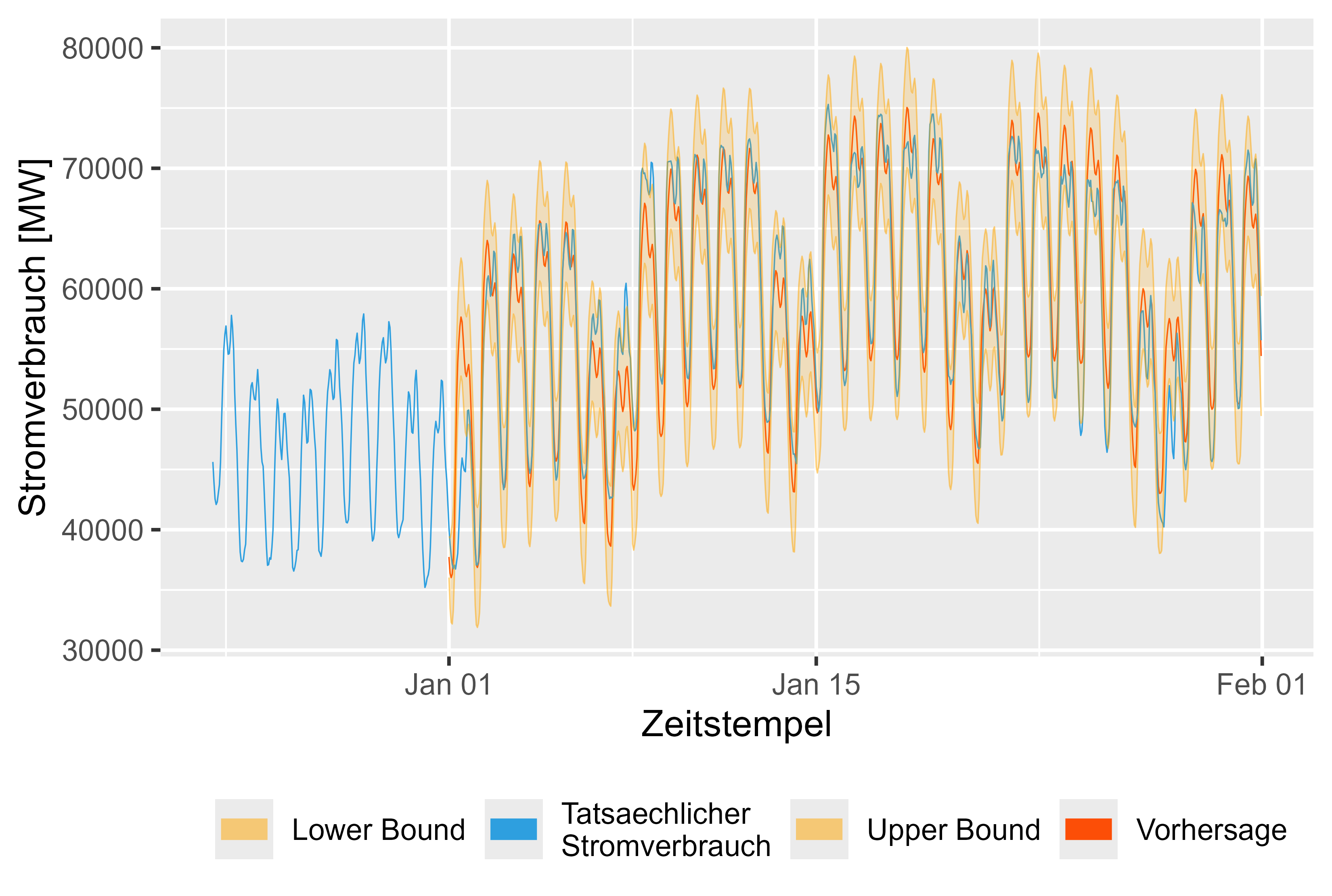Abbildung 16 Prognose vs. tatsächliche Werte LHM + DHR für Januar 2024
Auch die Residuen für das Modell im Vergleich zum SMARD-Modell sehen gut aus. Es gibt wenige Spitzen, die von Bedeutung sein könnten und durch Modellierung besser vorbereitet werden können. Aber insgesamt ein solides Ergebnis.
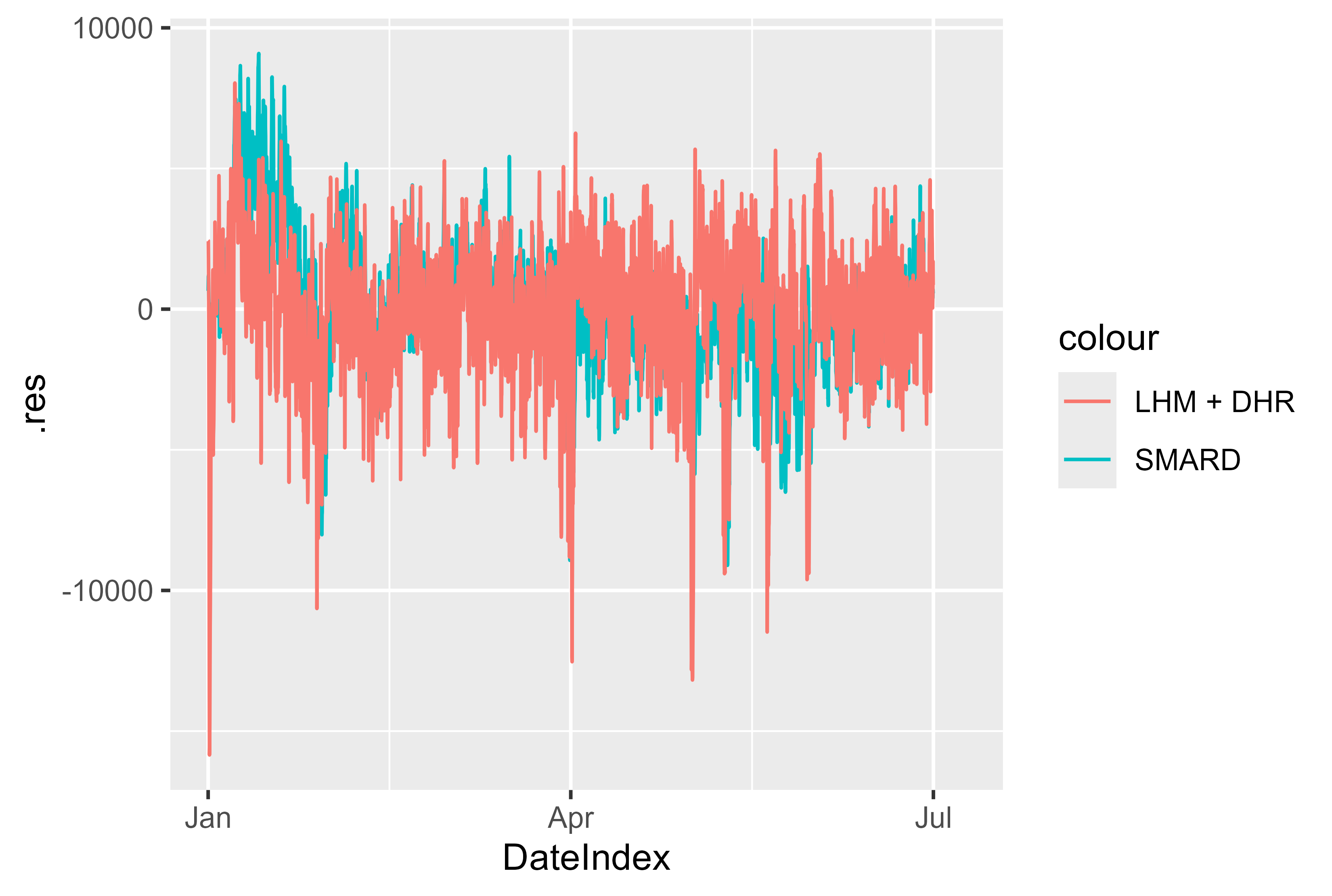Abbildung 17 Residuen LHM + DHR für Januar – Juli 2024
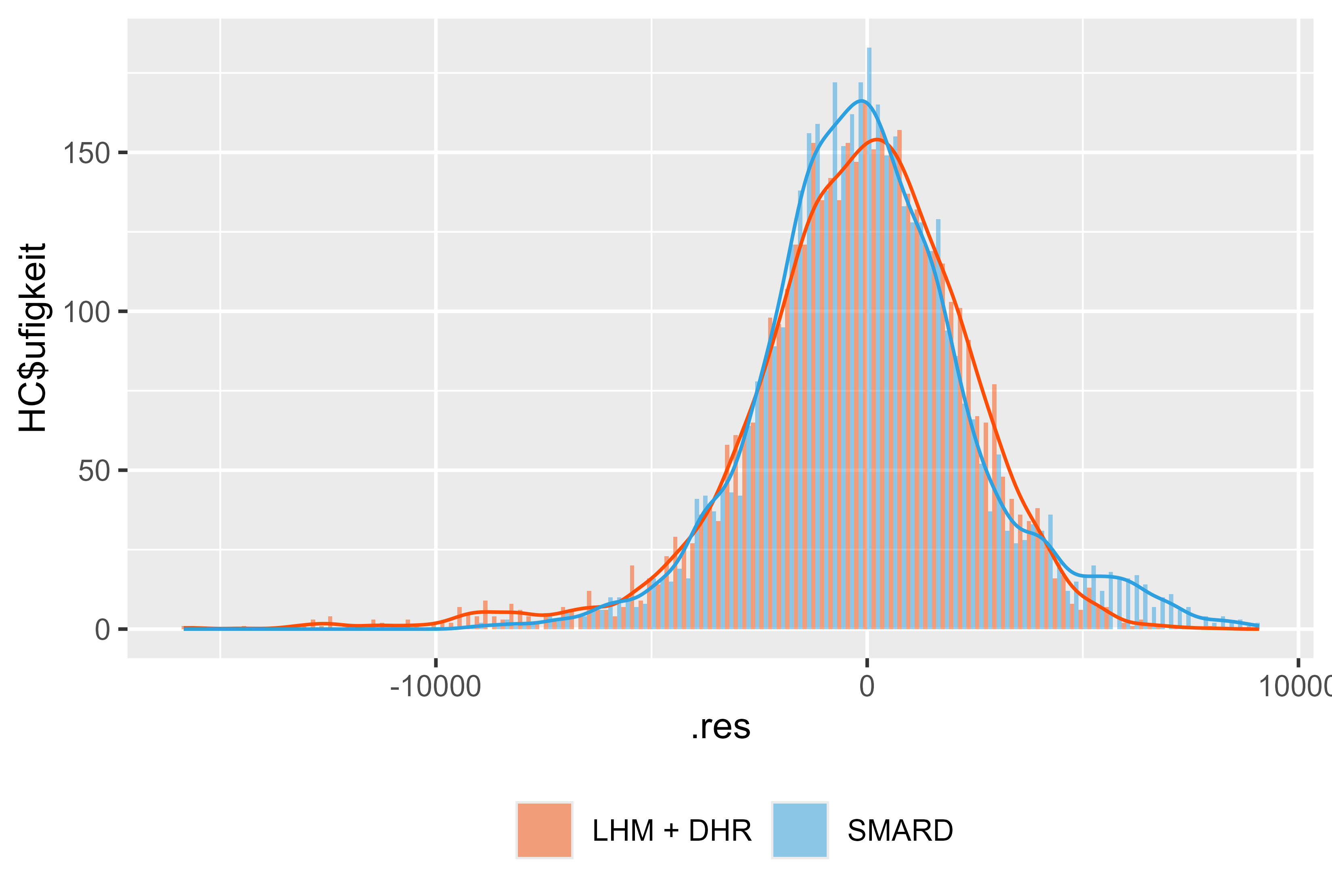Abbildung 18 Residuen LHM + DHR für Januar – Juli 2024
| Index | Modellname | RMSE | KARTE | MAE | Ensembleliert |
|---|---|---|---|---|---|
| 2 | Echte Beobachtungen | 0,000 | 0,000000 | 0,000 | WAHR |
| 3 | SMARD | 2480.693 | 3.602140 | 1869.466 | FALSCH |
| 4 | SMARD | 2480.693 | 3.602140 | 1869.466 | WAHR |
| 5 | Version_5 | 2626.807 | 3.816012 | 1937.670 | WAHR |
| 6 | version_0 | 2613.258 | 3,846888 | 1946.314 | WAHR |
| 7 | Version_7 | 2770.359 | 4.107272 | 2076.045 | WAHR |
| 8 | Version_8 | 2775.441 | 4.146788 | 2091.153 | WAHR |
| 9 | Version_9 | 2887.179 | 4.177841 | 2100.381 | WAHR |
| 10 | Version_6 | 2906.242 | 4.216517 | 2142.092 | WAHR |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSCH |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSCH |
| 13 | Version_4 | 2875.929 | 4.535388 | 2255.645 | WAHR |
| 14 | Version_2 | 2905.990 | 4.580770 | 2279.624 | WAHR |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | FALSCH |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSCH |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSCH |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSCH |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | FALSCH |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | FALSCH |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSCH |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSCH |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | FALSCH |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | FALSCH |
| 24 | prophet_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | FALSCH |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | FALSCH |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | FALSCH |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | FALSCH |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | FALSCH |
| 29 | Version_3 | 3546.729 | 5.064654 | 2570.530 | WAHR |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | FALSCH |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | FALSCH |
| 32 | version_1 | 4495.568 | 6.483477 | 3229.647 | WAHR |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | FALSCH |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | FALSCH |
| 35 | mean_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | FALSCH |
| 36 | naiv_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | FALSCH |
| 37 | drift_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | FALSCH |
NOTIZ:
Überprüfen Sie example/ensemble_model_2022_forecast oder example/ensemble_model_2023_forecast
Wir könnten weitere Faktoren einbeziehen wie:
