Löst das Turm-von-Hanoi-Rätsel durch Verstärkungslernen.
Führen Sie in einer Python-Umgebung mit installierten Numpy und Pandas das Skript hanoi.py aus, um die drei im Abschnitt „Ergebnisse“ angezeigten Diagramme zu erstellen. Das Skript kann leicht angepasst werden, um das Spiel beispielsweise mit einer anderen Anzahl an Scheiben N zu spielen.
Reinforcement Learning hat kürzlich neues Interesse geweckt, als AlphaGo von Google Deepmind einen professionellen menschlichen Go-Spieler besiegte. Hier wird ein einfacheres Rätsel gelöst: das Spiel Tower of Hanoi. Die Implementierung folgt dem Q-Learning-Algorithmus, wie er ursprünglich von Watkins & Dayan [1] vorgeschlagen wurde.
Das Spiel „Turm von Hanoi“ besteht aus drei Stiften und mehreren Scheiben unterschiedlicher Größe, die auf die Stifte geschoben werden können. Das Rätsel beginnt damit, dass alle Scheiben in aufsteigender Reihenfolge auf dem ersten Stift gestapelt werden, wobei die größte unten und die kleinste oben liegt. Ziel des Spiels ist es, alle Scheiben auf den dritten Stift zu bringen. Die einzigen zulässigen Züge sind solche, bei denen die oberste Scheibe von einem Stift auf einen anderen gebracht wird, mit der Einschränkung, dass eine Scheibe niemals auf eine kleinere Scheibe gelegt werden darf. Abbildung 1 zeigt die optimale Lösung für 4 Festplatten.

Abbildung 1. Eine animierte Lösung des Tower of Hanoi-Puzzles für 4 Scheiben. (Quelle: Wikipedia).
In Anlehnung an Anderson [2] stellen wir den Stand des Spiels durch Tupel dar, wobei das i -te Element angibt, auf welchem Stift sich die i -te Scheibe befindet. Die Festplatten sind in der Reihenfolge zunehmender Größe beschriftet. Somit ist der Anfangszustand (111) und der gewünschte Endzustand ist (333) (Abbildung 2).
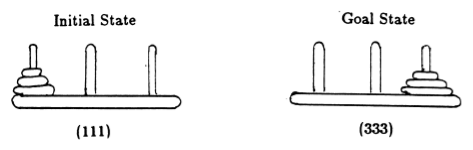
Abbildung 2. Anfangs- und Zielzustand des Tower of Hanoi-Puzzles mit 3 Scheiben. (Aus [2]).
Die Zustände des Puzzles und die Übergänge zwischen ihnen, die legalen Zügen entsprechen, bilden den Zustandsübergangsgraphen des Puzzles, der in Abbildung 3 dargestellt ist.
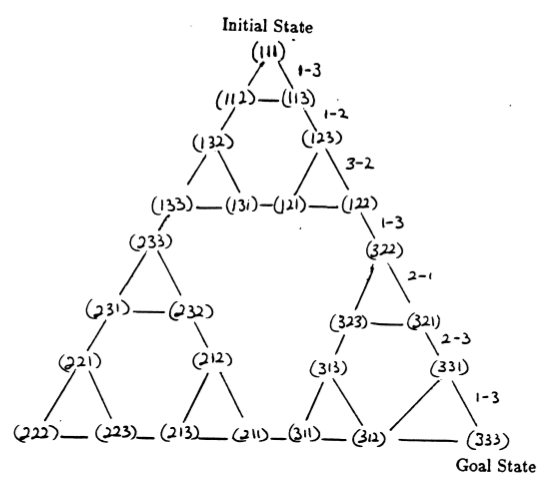
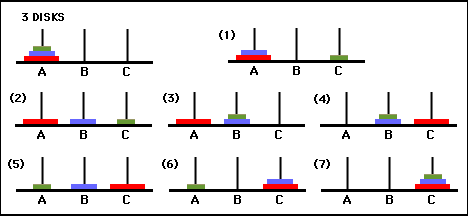
Abbildung 3. Zustandsübergangsdiagramm für das Drei-Scheiben-Puzzle „Turm von Hanoi“ (oben) und die entsprechende optimale 7-Züge-Lösung (unten), die dem Pfad auf der rechten Seite des Diagramms folgt. (Aus [2] und Mathforum.org).
Die Mindestanzahl an Zügen, die zum Lösen eines Turm-von-Hanoi-Rätsels erforderlich sind, beträgt 2 N - 1, wobei N die Anzahl der Scheiben ist. Für N = 3 kann das Rätsel also in 7 Zügen gelöst werden, wie in Abbildung 3 dargestellt. Im folgenden Abschnitt skizzieren wir, wie dies durch Q-Learning erreicht wird.
R und die „Aktionswert“-Matrix Q für 2 Festplatten Der erste Schritt im Programm besteht darin, eine Belohnungsmatrix R zu generieren, die die Spielregeln erfasst und eine Belohnung für den Sieg ausgibt. Der Einfachheit halber ist die Belohnungsmatrix in Abbildung 4 für N = 2 Festplatten dargestellt.
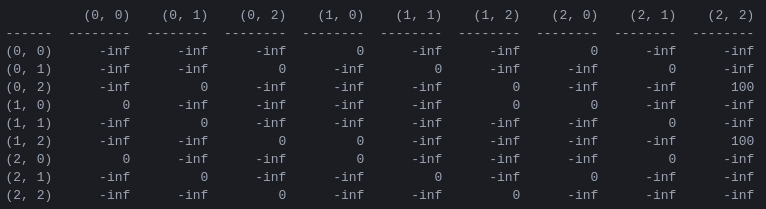
Abbildung 4. Belohnungsmatrix R für ein Tower of Hanoi-Puzzle mit N = 2 Scheiben. Das ( i , j )-te Element stellt die Belohnung für den Übergang vom Zustand i zum j dar. Die Zustände werden wie in den Abbildungen 2 und 3 durch Tupel gekennzeichnet, mit dem Unterschied, dass die Stifte „pythonisch“ von 0 bis 2 und nicht von 1 bis 3 indiziert werden. Bewegungen, die zum Zielzustand (2,2) führen, erhalten eine Belohnung von 100, illegale Züge von und alle anderen Züge von 0.
Die Belohnungsmatrix R beschreibt nur unmittelbare Belohnungen: Eine Belohnung von 100 kann nur aus den vorletzten Zuständen (0,2) und (1,2) erreicht werden. In den anderen Staaten hat jeder der 2 oder 3 möglichen Züge die gleiche Belohnung von 0, und es gibt keinen offensichtlichen Grund, einen der anderen vorzuziehen.
Letztendlich versuchen wir, jeder möglichen Bewegung in jedem Zustand einen „Wert“ zuzuordnen, sodass wir durch Maximierung dieser Werte eine Richtlinie definieren können, die zur optimalen Lösung führt. Die Matrix der „Werte“ für jede Aktion in jedem Zustand wird Q genannt und kann auf stochastische Weise rekursiv gelöst oder „gelernt“ werden, wie von Watkins & Dayan [1] beschrieben. Das Ergebnis für 2 Festplatten ist in Abbildung 5 dargestellt.
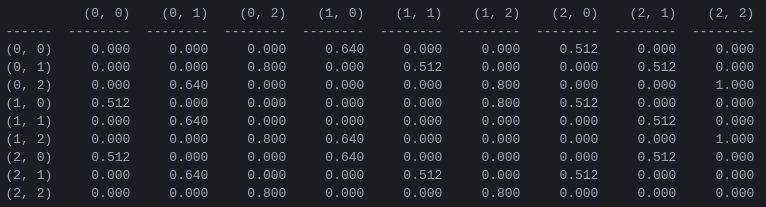
Abbildung 5. „Aktionswert“-Matrix Q für das Spiel „Tower of Hanoi“ mit 2 Scheiben, gelernt mit einem Abzinsungsfaktor = 0,8, einem Lernfaktor = 1,0 und 1000 Trainingsepisoden.
Die Werte der Matrix Q sind im Wesentlichen Gewichte, die den Eckpunkten des Zustandsübergangsgraphen in Abbildung 3 zugewiesen werden können und den Agenten auf dem kürzesten Weg vom Anfangszustand zum Zielzustand führen. In diesem Beispiel kann sich der Leser davon überzeugen, dass die Q Matrix den Agenten durch die Folge der Zustände (0,0) – (1) führt, indem er bei Zustand (0,0) beginnt und nacheinander die Bewegung mit dem höchsten Wert von Q auswählt ,0) - (1,2) - (2,2), was der optimalen 3-Züge-Lösung des 2-Scheiben-Spiels Tower of Hanoi entspricht (Abbildung 6).
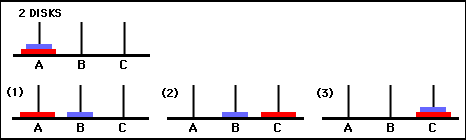
Abbildung 6. Lösung des Spiels „Turm von Hanoi“ mit 2 Scheiben. Die aufeinanderfolgenden Zustände werden durch (0,0), (1,0), (1,2) bzw. (2,2) dargestellt. (Quelle: mathforum.org).
In diesem Beispiel, in dem die Matrix Q ihrem optimalen Wert angenähert ist, definiert sie eine stationäre Richtlinie: Jede Zeile enthält eine Aktion mit einem eindeutigen Maximalwert. Während des Lernprozesses können jedoch verschiedene Aktionen denselben Wert von Q haben. (Dies ist insbesondere zu Beginn des Trainings der Fall, wenn Q auf eine Matrix aus Nullen initialisiert wird.) In den im folgenden Abschnitt vorgestellten Simulationen werden solche Situationen mit der folgenden stochastischen Richtlinie behandelt: In Fällen, in denen der maximale Q-Wert auf mehrere Aktionen verteilt ist, wählen Sie zufällig eine dieser Aktionen aus.
Die Leistung des Q-Learning-Algorithmus kann gemessen werden, indem die Anzahl der Züge gezählt wird, die (im Durchschnitt) erforderlich sind, um das Rätsel „Turm von Hanoi“ zu lösen. Diese Zahl nimmt mit der Anzahl der Trainingsepisoden ab, bis sie schließlich den optimalen Wert 2 N – 1 erreicht, wobei N die Anzahl der Festplatten ist, wie in Abbildung 7 für N = 2, 3 und 4 dargestellt.
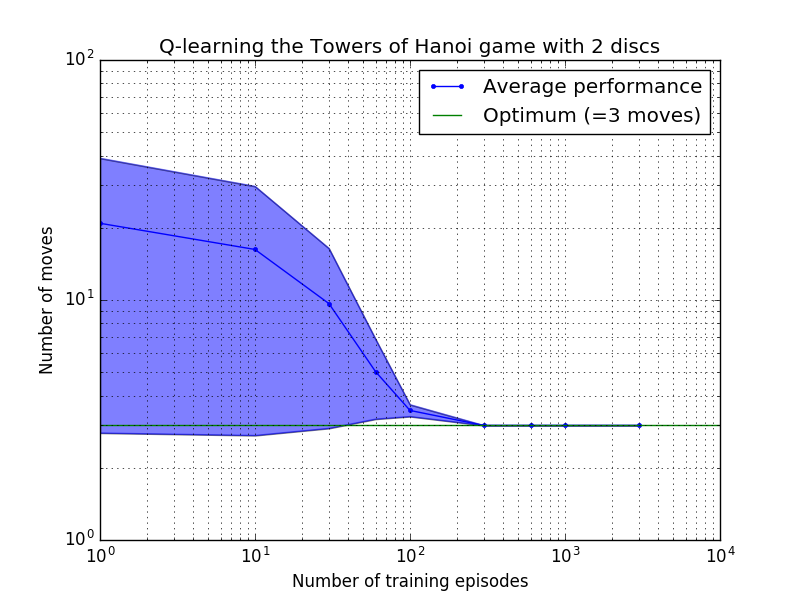
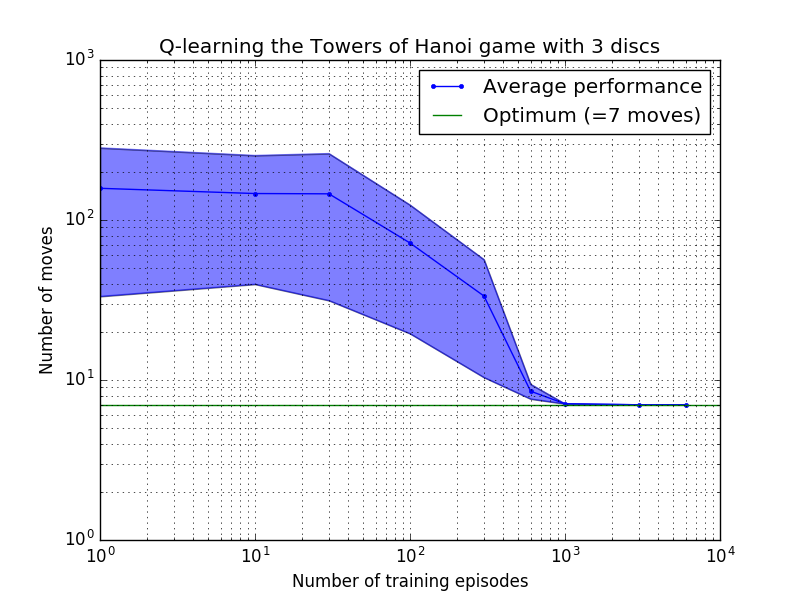
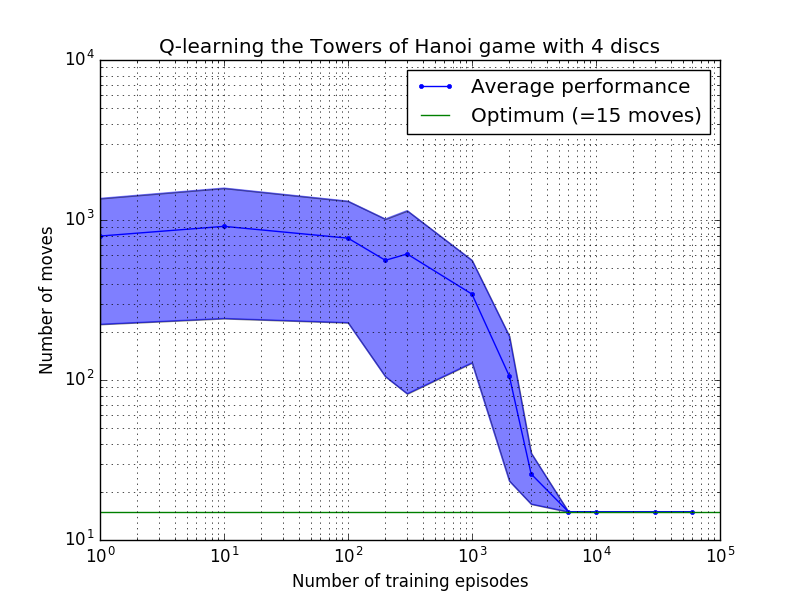
Abbildung 7. Leistung des Q-Learning-Algorithmus für das Spiel „Tower of Hanoi“ mit (von oben nach unten) 2, 3 und 4 Festplatten. In allen Fällen wurde mit einem Abzinsungsfaktor von = 0,8 und einem Lernfaktor von = 1,0 gelernt. Die durchgezogene blaue Kurve stellt die durchschnittliche Leistung über 100 Trainingsepochen und 100 Spiele des Spiels für jede resultierende stochastische Richtlinie dar. Die Ober- und Untergrenzen des blau schattierten Bereichs sind um die geschätzte Standardabweichung vom Mittelwert versetzt. (Für N = 3 und N = 4 wurden die Anzahl der Trainingsepisoden und die Spieldauer aufgrund rechnerischer Einschränkungen auf 10 bzw. 10 reduziert.)
Ein interessantes Merkmal der Lerneigenschaften in Abbildung 7 besteht darin, dass das Lernen in allen Fällen anfangs langsam ist und der Agent kaum besser abschneidet als die „Null-Training“-Politik, bei der Züge nach dem Zufallsprinzip ausgewählt werden. Irgendwann erreicht das Lernen einen „Wendepunkt“ und nähert sich dann in beschleunigtem Tempo der optimalen Anzahl von Zügen an (obwohl dies durch die logarithmische Skala etwas übertrieben ist).
Ein Python-Skript löst das Turm-von-Hanoi-Rätsel erfolgreich und optimal für eine beliebige Anzahl von Datenträgern durch Q-Learning. Das Skript kann leicht an andere Probleme mit einer anderen Belohnungsmatrix R angepasst werden.
Die Anzahl der Trainingsepisoden, die erforderlich sind, um zu einer optimalen Lösung zu konvergieren, steigt stark mit der Anzahl der Festplatten N : Für N=2 Festplatten sind etwa 300 Episoden erforderlich, während für N=4 etwa 6.000 erforderlich sind. Eine mögliche Verbesserung des Lernalgorithmus bestünde darin, ihm die automatische Suche nach rekursiven Lösungen zu ermöglichen, wie es von Hengst [3] durchgeführt wurde.
[ 1 ] Watkins & Dayan, Q-Learning , Machine Learning, 8, 279-292 (1992). (PDF).
[2] Anderson, Lernen und Problemlösung mit mehrschichtigen konnektionistischen Systemen , Ph.D. Dissertation (1986). (PDF).
[ 3 ] Hengst, Discovering Hierarchy in Reinforcement Learning with HEXQ , Proceedings on the Nineteenth International Conference on Machine Learning (2002). (PDF).