ai simplest network
1.0.0
Dies ist das einfachste künstliche neuronale Netzwerk, das erklärt und demonstriert werden kann.
Künstliche neuronale Netze sind vom Gehirn inspiriert, indem miteinander verbundene künstliche Neuronen Muster speichern und miteinander kommunizieren. Die einfachste Form eines künstlichen Neurons verfügt über einen oder mehrere Eingänge 
jedes hat ein bestimmtes Gewicht 
und ein Ausgang 
.
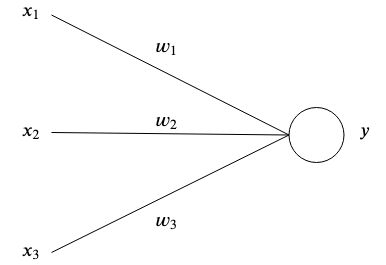
Auf der einfachsten Ebene ist der Output die Summe seiner Inputs multipliziert mit seinen Gewichten.
Der Zweck eines Netzwerks besteht darin, eine bestimmte Ausgabe zu lernen bestimmte Eingabe(n) gegeben 
durch Approximation einer komplexen Funktion mit vielen Parametern 
dass wir uns das nicht ausdenken konnten.
Angenommen, wir haben ein Netzwerk mit zwei Eingängen 
Und 
und zwei Gewichte 
Und 
.
Die Idee besteht darin, die Gewichte so anzupassen, dass die gegebenen Eingaben die gewünschte Ausgabe erzeugen.
Gewichte werden normalerweise zufällig initialisiert, da wir ihren optimalen Wert nicht im Voraus kennen können. Der Einfachheit halber werden wir sie jedoch beide initialisieren 
.
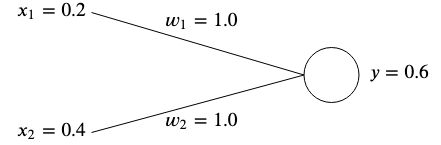
Wenn wir die Ausgabe dieses Netzwerks berechnen, erhalten wir
Wenn die Ausgabe nicht mit dem erwarteten Zielwert übereinstimmt, liegt ein Fehler vor.
Wenn wir beispielsweise einen Zielwert von erhalten wollten 
dann hätten wir einen Unterschied von
Eine gängige Methode zur Messung des Fehlers (auch als Kostenfunktion bezeichnet) ist die Verwendung des mittleren quadratischen Fehlers:
Wenn wir mehrere Zuordnungen von Eingaben und Zielwerten hätten, wird der Fehler zur durchschnittlichen Summe jeder Zuordnung.
Wir verwenden den mittleren quadratischen Fehler, um zu messen, wie weit die Ergebnisse von unserem gewünschten Ziel entfernt sind. Durch die Quadrierung werden negative Vorzeichen entfernt und größere Unterschiede zwischen Ausgabe und Ziel werden stärker gewichtet.
Um den Fehler zu beheben, müssten wir die Gewichte so anpassen, dass die Ausgabe unserem Ziel entspricht. In unserem Beispiel Tieferlegung aus 
Zu 
würde den Zweck erfüllen, da
Um jedoch die Gewichte unserer neuronalen Netze für viele verschiedene Eingaben und Zielwerte anzupassen, benötigen wir einen Lernalgorithmus, der dies automatisch für uns erledigt.
Die Idee besteht darin, anhand des Fehlers zu verstehen, wie jedes Gewicht angepasst werden sollte, damit der Fehler minimiert wird. Zunächst müssen wir jedoch etwas über Gradienten lernen.
Es handelt sich im Wesentlichen um einen Vektor, der auf die Richtung des steilsten Anstiegs einer Funktion zeigt. Der Gradient wird mit bezeichnet 
und ist einfach die partielle Ableitung jeder Variablen einer als Vektor ausgedrückten Funktion.
Für eine Funktion mit zwei Variablen sieht das so aus:
Lassen Sie uns einige Zahlen eingeben und den Gradienten anhand eines einfachen Beispiels berechnen. Angenommen, wir haben eine Funktion 
, dann wäre der Gradient
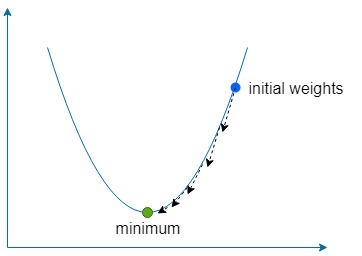
Der Abstiegsteil bedeutet einfach, den Gradienten zu verwenden, um die Richtung des steilsten Anstiegs unserer Funktion zu ermitteln, und dann mehrmals um einen kleinen Betrag in die entgegengesetzte Richtung zu gehen, um das globale (oder manchmal lokale) Minimum der Funktion zu ermitteln.
Wir verwenden eine Konstante namens Lernrate , die mit bezeichnet wird 
um zu definieren, wie klein der Schritt in diese Richtung sein soll.
Wenn zu groß ist, besteht die Gefahr, dass wir das Funktionsminimum überschreiten. Wenn es jedoch zu niedrig ist, dauert das Lernen des Netzwerks länger und wir laufen Gefahr, in einem flachen lokalen Minimum stecken zu bleiben.
Für unsere beiden Gewichte Und Wir müssen den Gradienten dieser Gewichte in Bezug auf die Fehlerfunktion ermitteln 
Für beides Und , können wir den Gradienten mithilfe der Kettenregel ermitteln
Von nun an bezeichnen wir die 
als die 
Bezeichnung für Einfachheit.
Sobald wir den Gradienten haben, können wir unsere Gewichte aktualisieren, indem wir den berechneten Gradienten multipliziert mit der Lernrate subtrahieren.
Und wir wiederholen diesen Vorgang, bis der Fehler minimiert ist und nahe genug bei Null liegt.
Das enthaltene Beispiel lehrt den folgenden Datensatz einem neuronalen Netzwerk mit zwei Eingaben und einer Ausgabe mithilfe eines Gradientenabstiegs:
Sobald das Netzwerk gelernt hat, sollte es ~0 ausgeben, wenn zwei gegeben sind s und ~ wenn gegeben a und a 
.
docker build -t simplest-network .
docker run --rm simplest-network
