7 einfache JavaScript-Funktionen, die Ihnen ein Gefühl dafür vermitteln, wie Maschinen tatsächlich „lernen“ können.
In anderen Sprachen: Русский, Português
Vielleicht interessiert Sie auch ? Interaktive Experimente zum maschinellen Lernen
NanoNeuron ist eine stark vereinfachte Version des Neuron-Konzepts von Neural Networks. NanoNeuron ist darauf trainiert, Temperaturwerte von Celsius in Fahrenheit umzuwandeln.
Das NanoNeuron.js-Codebeispiel enthält 7 einfache JavaScript-Funktionen (die sich mit Modellvorhersage, Kostenberechnung, Vorwärts-/Rückwärtsausbreitung und Training befassen), die Ihnen ein Gefühl dafür vermitteln, wie Maschinen tatsächlich „lernen“ können. Keine Bibliotheken von Drittanbietern, keine externen Datensätze oder Abhängigkeiten, nur reine und einfache JavaScript-Funktionen.
☝?Diese Funktionen sind keineswegs eine vollständige Anleitung zum maschinellen Lernen. Viele Konzepte des maschinellen Lernens werden übersprungen und zu stark vereinfacht! Diese Vereinfachung erfolgt mit Absicht, um dem Leser ein wirklich grundlegendes Verständnis und Gefühl dafür zu vermitteln, wie Maschinen lernen können, und um dem Leser letztendlich zu ermöglichen, zu erkennen, dass es sich nicht um „Magie des maschinellen Lernens“, sondern um „Mathematik des maschinellen Lernens“ handelt.
Sie haben wahrscheinlich schon von Neuronen im Zusammenhang mit neuronalen Netzen gehört. NanoNeuron ist genau das, aber einfacher und wir werden es von Grund auf implementieren. Der Einfachheit halber werden wir nicht einmal ein Netzwerk auf NanoNeurons aufbauen. Wir werden alles von selbst funktionieren lassen und einige magische Vorhersagen für uns treffen. Wir werden diesem einzigartigen NanoNeuron nämlich beibringen, die Temperatur von Celsius in Fahrenheit umzurechnen (vorherzusagen).
Die Formel zur Umrechnung von Celsius in Fahrenheit lautet übrigens wie folgt:
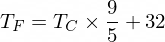
Aber im Moment weiß unser NanoNeuron nichts davon ...
Lassen Sie uns unsere NanoNeuron-Modellfunktion implementieren. Es implementiert eine grundlegende lineare Abhängigkeit zwischen x und y , die wie folgt aussieht: y = w * x + b . Einfach ausgedrückt ist unser NanoNeuron ein „Kind“ in einer „Schule“, dem beigebracht wird, die gerade Linie in XY -Koordinaten zu zeichnen.
Die Variablen w , b sind Parameter des Modells. NanoNeuron kennt nur diese beiden Parameter der linearen Funktion. Diese Parameter wird NanoNeuron während des Trainingsprozesses „lernen“.
Das Einzige, was NanoNeuron tun kann, ist, lineare Abhängigkeiten zu imitieren. In seiner predict() Methode akzeptiert es eine Eingabe x und sagt die Ausgabe y voraus. Hier gibt es keine Magie.
function NanoNeuron ( w , b ) {
this . w = w ;
this . b = b ;
this . predict = ( x ) => {
return x * this . w + this . b ;
}
}(... warte... lineare Regression, bist du es?) ?
Der Temperaturwert in Celsius kann mit der folgenden Formel in Fahrenheit umgerechnet werden: f = 1.8 * c + 32 , wobei c eine Temperatur in Celsius und f die berechnete Temperatur in Fahrenheit ist.
function celsiusToFahrenheit ( c ) {
const w = 1.8 ;
const b = 32 ;
const f = c * w + b ;
return f ;
} ; Letztendlich wollen wir unserem NanoNeuron beibringen, diese Funktion zu imitieren (um zu lernen, dass w = 1.8 und b = 32 ), ohne diese Parameter im Voraus zu kennen.
So sieht die Umrechnungsfunktion von Celsius in Fahrenheit aus:
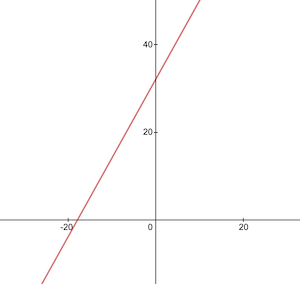
Vor dem Training müssen wir Trainings- und Testdatensätze basierend auf der Funktion celsiusToFahrenheit() generieren. Datensätze bestehen aus Paaren von Eingabewerten und korrekt beschrifteten Ausgabewerten.
Im wirklichen Leben würden diese Daten in den meisten Fällen gesammelt und nicht generiert. Beispielsweise könnten wir eine Reihe von Bildern mit handgezeichneten Zahlen und den entsprechenden Zahlensatz haben, der erklärt, welche Zahl auf jedem Bild steht.
Wir werden TRAINING-Beispieldaten verwenden, um unser NanoNeuron zu trainieren. Bevor unser NanoNeuron wachsen und selbstständig Entscheidungen treffen kann, müssen wir ihm anhand von Trainingsbeispielen beibringen, was richtig und was falsch ist.
Wir werden TEST-Beispiele verwenden, um zu bewerten, wie gut unser NanoNeuron mit den Daten umgeht, die es während des Trainings nicht gesehen hat. An diesem Punkt konnten wir sehen, dass unser „Kind“ erwachsen geworden ist und selbstständig Entscheidungen treffen kann.
function generateDataSets ( ) {
// xTrain -> [0, 1, 2, ...],
// yTrain -> [32, 33.8, 35.6, ...]
const xTrain = [ ] ;
const yTrain = [ ] ;
for ( let x = 0 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTrain . push ( x ) ;
yTrain . push ( y ) ;
}
// xTest -> [0.5, 1.5, 2.5, ...]
// yTest -> [32.9, 34.7, 36.5, ...]
const xTest = [ ] ;
const yTest = [ ] ;
// By starting from 0.5 and using the same step of 1 as we have used for training set
// we make sure that test set has different data comparing to training set.
for ( let x = 0.5 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTest . push ( x ) ;
yTest . push ( y ) ;
}
return [ xTrain , yTrain , xTest , yTest ] ;
} Wir benötigen eine Metrik, die uns zeigt, wie nahe die Vorhersage unseres Modells an den korrekten Werten liegt. Die Berechnung der Kosten (des Fehlers) zwischen dem korrekten Ausgabewert von y und prediction , die unser NanoNeuron erstellt hat, erfolgt anhand der folgenden Formel:
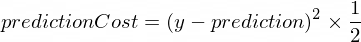
Dies ist ein einfacher Unterschied zwischen zwei Werten. Je näher die Werte beieinander liegen, desto geringer ist der Unterschied. Wir verwenden hier eine Potenz von 2 nur um negative Zahlen loszuwerden, sodass (1 - 2) ^ 2 dasselbe wäre wie (2 - 1) ^ 2 . Die Division durch 2 erfolgt nur, um die Formel für die Rückwärtsausbreitung weiter zu vereinfachen (siehe unten).
Die Kostenfunktion ist in diesem Fall so einfach wie:
function predictionCost ( y , prediction ) {
return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
} Eine Vorwärtsausbreitung durchzuführen bedeutet, eine Vorhersage für alle Trainingsbeispiele aus xTrain und yTrain -Datensätzen zu erstellen und die durchschnittlichen Kosten dieser Vorhersagen auf dem Weg zu berechnen.
Wir lassen an dieser Stelle einfach unser NanoNeuron seine Meinung äußern, indem wir es einfach raten lassen, wie die Temperatur umgerechnet werden soll. Hier könnte es dummerweise falsch sein. Die durchschnittlichen Kosten werden uns zeigen, wie falsch unser Modell derzeit ist. Dieser Kostenwert ist wirklich wichtig, da die NanoNeuron-Parameter w und b geändert werden und die Vorwärtsausbreitung erneut durchgeführt wird. Wir werden in der Lage sein zu beurteilen, ob unser NanoNeuron intelligenter geworden ist oder nicht, nachdem sich diese Parameter geändert haben.
Die durchschnittlichen Kosten werden nach folgender Formel berechnet:
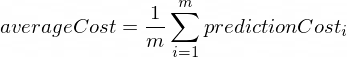
Wobei m eine Anzahl von Trainingsbeispielen ist (in unserem Fall: 100 ).
So können wir es im Code implementieren:
function forwardPropagation ( model , xTrain , yTrain ) {
const m = xTrain . length ;
const predictions = [ ] ;
let cost = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
cost += predictionCost ( yTrain [ i ] , prediction ) ;
predictions . push ( prediction ) ;
}
// We are interested in average cost.
cost /= m ;
return [ predictions , cost ] ;
}Was sollten wir tun, um die Vorhersagen präziser zu machen, wenn wir wissen, wie richtig oder falsch die Vorhersagen unseres NanoNeurons sind (basierend auf den durchschnittlichen Kosten zu diesem Zeitpunkt)?
Die Rückwärtsausbreitung gibt uns die Antwort auf diese Frage. Bei der Rückwärtsausbreitung werden die Kosten einer Vorhersage bewertet und die Parameter w und b des NanoNeurons angepasst, damit die nächsten und zukünftigen Vorhersagen präziser sind.
Hier sieht maschinelles Lernen wie Magie aus ?♂️. Das Schlüsselkonzept hier ist die Ableitung , die zeigt, welcher Schritt unternommen werden muss, um dem Kostenfunktionsminimum näher zu kommen.
Denken Sie daran, dass das ultimative Ziel des Trainingsprozesses das Finden der minimalen Kostenfunktion ist. Wenn wir solche Werte für w und b finden, dass unsere Durchschnittskostenfunktion klein ist, würde das bedeuten, dass das NanoNeuron-Modell wirklich gute und präzise Vorhersagen macht.
Derivate sind ein großes und separates Thema, das wir in diesem Artikel nicht behandeln werden. MathIsFun ist eine gute Ressource, um ein grundlegendes Verständnis davon zu erlangen.
Eine Sache bei Ableitungen, die Ihnen helfen wird zu verstehen, wie die Rückwärtsausbreitung funktioniert, ist, dass die Ableitung ihrer Bedeutung nach eine Tangente an die Funktionskurve ist, die in die Richtung des Funktionsminimums zeigt.
Bildquelle: MathIsFun
Im Diagramm oben können Sie beispielsweise sehen, dass die Steigung uns sagt, dass wir left und down gehen müssen, um zum Funktionsminimum zu gelangen, wenn wir uns am Punkt (x=2, y=4) befinden. Beachten Sie auch, dass wir uns umso schneller zum Minimum bewegen sollten, je größer die Steigung ist.
Die Ableitungen unserer averageCost -Funktion für die Parameter w und b sehen folgendermaßen aus:
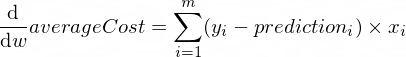
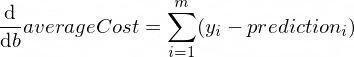
Wobei m eine Anzahl von Trainingsbeispielen ist (in unserem Fall: 100 ).
Weitere Informationen zu Ableitungsregeln und zur Ableitung komplexer Funktionen finden Sie hier.
function backwardPropagation ( predictions , xTrain , yTrain ) {
const m = xTrain . length ;
// At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
// Therefore we're setting up the changing steps for each parameters to 0.
let dW = 0 ;
let dB = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
dB += yTrain [ i ] - predictions [ i ] ;
}
// We're interested in average deltas for each params.
dW /= m ;
dB /= m ;
return [ dW , dB ] ;
} Jetzt wissen wir, wie wir die Korrektheit unseres Modells für alle Trainingssatzbeispiele bewerten können ( Vorwärtsausbreitung ). Wir wissen auch, wie wir kleine Anpassungen an den Parametern w und b unseres NanoNeuron-Modells vornehmen können ( Rückwärtsausbreitung ). Das Problem ist jedoch, dass es für unser Modell nicht ausreicht, Gesetze/Trends aus den Trainingsdaten zu lernen, wenn wir die Vorwärtsausbreitung und dann die Rückwärtsausbreitung nur einmal ausführen. Man kann es damit vergleichen, dass das Kind einen Tag lang die Grundschule besucht. Er/sie sollte nicht nur einmal, sondern Tag für Tag und Jahr für Jahr zur Schule gehen, um etwas zu lernen.
Daher müssen wir die Vorwärts- und Rückwärtsausbreitung für unser Modell viele Male wiederholen. Genau das macht die Funktion trainModel() . Es ist wie ein „Lehrer“ für unser NanoNeuron-Modell:
epochs ) mit unserem etwas dummen NanoNeuron-Modell verbringen und versuchen, es zu trainieren/zu lehren,xTrain und yTrain -Datensätze) für das Training verwendet.alpha verwendet Ein paar Worte zur Lernrate alpha . Dies ist lediglich ein Multiplikator für dW und dB -Werte, die wir während der Rückwärtsausbreitung berechnet haben. Die Ableitung zeigte uns also die Richtung, die wir einschlagen müssen, um ein Minimum der Kostenfunktion zu finden ( dW und dB Vorzeichen), und sie zeigte uns auch, wie schnell wir in diese Richtung gehen müssen (absolute Werte von dW und dB ). Jetzt müssen wir diese Schrittgrößen mit alpha multiplizieren, um unsere Bewegung schneller oder langsamer auf das Minimum anzupassen. Wenn wir große Werte für alpha verwenden, überspringen wir manchmal einfach das Minimum und finden es nie.
Die Analogie zum Lehrer wäre, dass unser „Nano-Kind“ umso schneller lernt, je mehr er/sie unser „Nano-Kind“ fordert. Wenn der Lehrer jedoch zu viel Druck ausübt, erleidet das „Kind“ einen Nervenzusammenbruch und gewinnt. Ich kann nichts lernen?
So aktualisieren wir die w und b -Parameter unseres Modells:
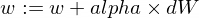
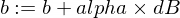
Und hier ist unsere Trainerfunktion:
function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
// The is the history array of how NanoNeuron learns.
const costHistory = [ ] ;
// Let's start counting epochs.
for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
// Forward propagation.
const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
costHistory . push ( cost ) ;
// Backward propagation.
const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
// Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
nanoNeuron . w += alpha * dW ;
nanoNeuron . b += alpha * dB ;
}
return costHistory ;
}Nun nutzen wir die Funktionen, die wir oben erstellt haben.
Erstellen wir unsere NanoNeuron-Modellinstanz. Zu diesem Zeitpunkt weiß das NanoNeuron nicht, welche Werte für die Parameter w und b eingestellt werden sollen. Also lasst uns w und b zufällig einrichten.
const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;Generieren Sie Trainings- und Testdatensätze.
const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ; Lassen Sie uns das Modell mit kleinen inkrementellen Schritten ( 0.0005 ) für 70000 Epochen trainieren. Mit diesen Parametern kann man spielen, sie werden empirisch definiert.
const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;Sehen wir uns an, wie sich die Kostenfunktion während des Trainings verändert hat. Wir gehen davon aus, dass die Kosten nach der Schulung deutlich niedriger sein werden als vorher. Das würde bedeuten, dass NanoNeuron intelligenter geworden wäre. Auch das Gegenteil ist möglich.
console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024 Auf diese Weise ändern sich die Schulungskosten im Laufe der Epochen. Auf der x Achse ist die Epochenzahl x1000 angegeben.
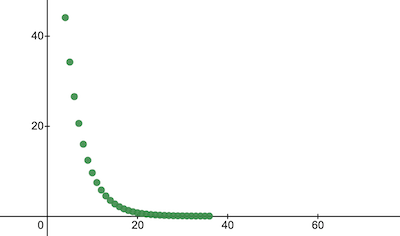
Werfen wir einen Blick auf die Parameter von NanoNeuron, um zu sehen, was es gelernt hat. Wir gehen davon aus, dass die NanoNeuron-Parameter w und b denen ähneln, die wir in der Funktion celsiusToFahrenheit() haben ( w = 1.8 und b = 32 ), da unser NanoNeuron versucht hat, sie zu imitieren.
console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}Bewerten Sie die Modellgenauigkeit für den Testdatensatz, um zu sehen, wie gut unser NanoNeuron mit neuen unbekannten Datenvorhersagen umgeht. Es wird erwartet, dass die Kosten für Vorhersagen auf Testsätzen nahe an den Trainingskosten liegen. Dies würde bedeuten, dass unser NanoNeuron bei bekannten und unbekannten Daten eine gute Leistung erbringt.
[ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023Da wir nun sehen, dass unser NanoNeuron-„Kind“ in der „Schule“ während des Trainings gute Leistungen erbracht hat und dass er Temperaturen von Celsius in Fahrenheit korrekt umrechnen kann, selbst für die Daten, die es nicht gesehen hat, können wir es als „intelligent“ bezeichnen. und stelle ihm ein paar Fragen. Dies war das ultimative Ziel des gesamten Trainingsprozesses.
const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158So nah! Wie wir alle Menschen ist unser NanoNeuron gut, aber nicht ideal :)
Viel Spaß beim Lernen!
Sie können das Repository klonen und lokal ausführen:
git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuronnode ./NanoNeuron.jsDie folgenden Konzepte des maschinellen Lernens wurden zur Vereinfachung der Erklärung übersprungen und vereinfacht.
Aufteilung von Trainings-/Testdatensätzen
Normalerweise haben Sie einen großen Datensatz. Abhängig von der Anzahl der Beispiele in diesem Satz möchten Sie ihn möglicherweise im Verhältnis 70/30 für Zug-/Testsätze aufteilen. Die Daten im Satz sollten vor der Aufteilung zufällig gemischt werden. Wenn die Anzahl der Beispiele groß ist (z. B. Millionen), kann die Aufteilung bei Trainings-/Testdatensätzen in Verhältnissen erfolgen, die eher bei 90/10 oder 95/5 liegen.
Das Netzwerk bringt die Kraft
Normalerweise werden Sie die Verwendung nur eines eigenständigen Neurons nicht bemerken. Die Kraft liegt im Netzwerk solcher Neuronen. Das Netzwerk könnte viel komplexere Funktionen lernen. NanoNeuron allein ähnelt eher einer einfachen linearen Regression als einem neuronalen Netzwerk.
Eingabenormalisierung
Vor dem Training wäre es besser, die Eingabewerte zu normalisieren.
Vektorisierte Implementierung
Bei Netzwerken funktionieren die vektorisierten (Matrix-)Berechnungen viel schneller als for Schleifen. Normalerweise funktioniert die Vorwärts-/Rückwärtsausbreitung viel schneller, wenn sie in vektorisierter Form implementiert und beispielsweise mithilfe der Numpy-Python-Bibliothek berechnet wird.
Minimum der Kostenfunktion
Die Kostenfunktion, die wir in diesem Beispiel verwendet haben, ist zu stark vereinfacht. Es sollte logarithmische Komponenten haben. Durch eine Änderung der Kostenfunktion ändern sich auch deren Ableitungen, sodass auch im Rückwärtsausbreitungsschritt andere Formeln verwendet werden.
Aktivierungsfunktion
Normalerweise sollte die Ausgabe eines Neurons durch eine Aktivierungsfunktion wie Sigmoid oder ReLU oder andere geleitet werden.