Matrix mit einem neuronalen Netzwerk umkehren.
Inverting Matrices stellt neuronale Netzwerke vor, hauptsächlich aufgrund der inhärenten Einschränkungen bei der Durchführung präziser arithmetischer Operationen wie Multiplikation und Aufteilung auf Aktivierungen. Herkömmliche dichte Netzwerke benötigen häufig Hilfe bei diesen Aufgaben, da sie nicht explizit für die Komplexität der Matrixinversion ausgelegt sind. Experimente mit einfachen dichten neuronalen Netzwerken haben signifikante Schwierigkeiten gezeigt, genaue Matrixinversionen zu erreichen. Trotz verschiedener Versuche, den Architektur und den Trainingsprozess zu optimieren, müssen die Ergebnisse häufig verbessert werden. Der Übergang zu einer komplexeren Architektur-einem 7-Schicht-Restnetzwerk (RESNET)-kann jedoch zu deutlichen Verbesserungen der Leistung führen.
Die RESNET -Architektur, die für ihre Fähigkeit bekannt ist, tiefe Darstellungen durch verbleibende Verbindungen zu lernen, hat sich als wirksam bei der Anpassung der Matrixinversion als wirksam erwiesen. Bei Millionen von Parametern kann dieses Netzwerk komplizierte Muster innerhalb der Daten erfassen, die einfachere Modelle nicht können. Diese Komplexität hat jedoch Kosten: Für eine effektive Verallgemeinerung sind erhebliche Schulungsdaten erforderlich.
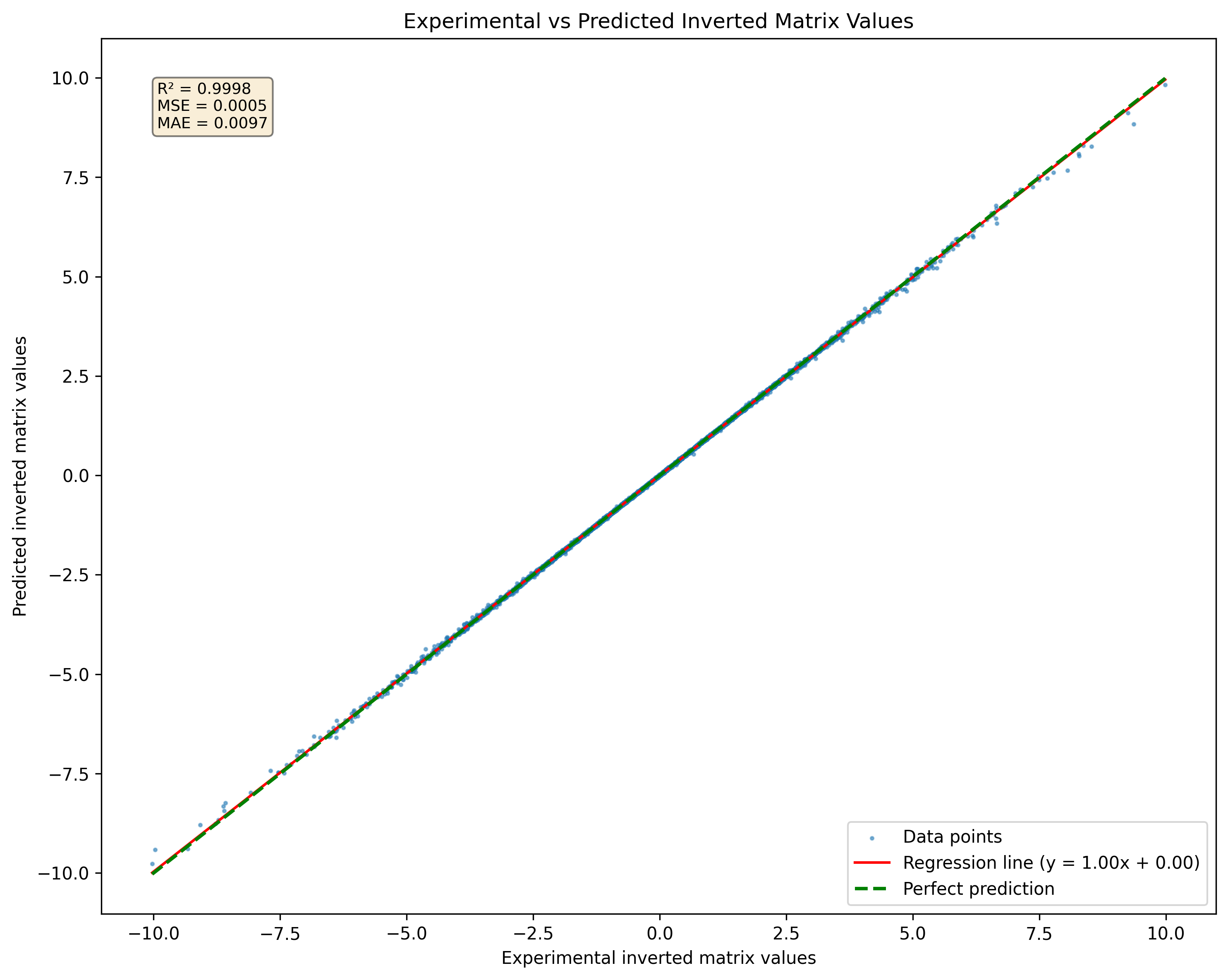Abbildung 1: Visualisierung eines neuronalen Netzwerks vorhergesagt invertierte Matrix für eine Reihe von Matrizen 3x3, die im Datensatz noch nie gesehen wurden
Um die Leistung des neuronalen Netzwerks bei der Vorhersage von Matrixinversionen zu bewerten, wird eine spezifische Verlustfunktion verwendet:
In dieser Gleichung:
Ziel ist es, die Differenz zwischen der Identitätsmatrix und dem Produkt der ursprünglichen Matrix und ihrer vorhergesagten Umkehrung zu minimieren. Diese Verlustfunktion misst effektiv, wie nahe die vorhergesagte Inverse an genau ist.
Zusätzlich, wenn
Diese Verlustfunktion bietet unterschiedliche Vorteile gegenüber herkömmlichen Verlustfunktionen wie dem mittleren quadratischen Fehler (MSE) oder dem mittleren absoluten Fehler (MAE).
Direkte Messung der Inversiongenauigkeit Das Hauptziel der Matrixinversion besteht darin, sicherzustellen, dass das Produkt einer Matrix und ihre Inverse die Identitätsmatrix ergibt. Die Verlustfunktion erfasst diese Anforderung direkt, indem die Abweichung von der Identitätsmatrix gemessen wird. Im Gegensatz dazu konzentrieren sich MSE und MAE auf die Unterschiede zwischen vorhergesagten Werten und wahren Werten, ohne die grundlegende Eigenschaft der Matrixinversion explizit zu beheben.
Betonung der strukturellen Integrität durch Verwendung einer Verlustfunktion, die bewertet, wie nahe das Produkt AA - 1AA - 1 an II ist, betont es die Aufrechterhaltung der strukturellen Integrität der beteiligten Matrizen. Dies ist besonders wichtig in Anwendungen, bei denen die Konservierung linearer Beziehungen von entscheidender Bedeutung ist. Traditionelle Verlustfunktionen wie MSE und MAE berücksichtigen diesen strukturellen Aspekt nicht, was möglicherweise zu Lösungen führt, die den Fehler minimieren, aber die mathematischen Anforderungen der Matrixinversion nicht erfüllen.
Anwendbarkeit auf nicht singuläre Matrizen Diese Verlustfunktion geht von Natur aus davon aus, dass die invertierten Matrizen nicht singulär sind (dh invertierbar). In Szenarien, in denen einzigartige Matrizen vorhanden sind, können traditionelle Verlustfunktionen irreführende Ergebnisse erzielen, da sie nicht die Unmöglichkeit berücksichtigen, eine gültige Inverse zu erhalten. Die vorgeschlagene Verlustfunktion unterstreicht diese Einschränkung, indem sie größere Fehler erzeugen, wenn versucht wird, einzelne Matrizen zu invertieren.
Eine signifikante Einschränkung bei der Verwendung neuronaler Netzwerke zur Matrixinversion ist ihre Unfähigkeit, Singularmatrizen effektiv zu bewältigen. Eine einzigartige Matrix hat keine Umkehrung; Jeder Versuch eines neuronalen Netzwerks, eine Umkehrung für solche Matrizen vorherzusagen, liefert daher falsche Ergebnisse. In der Praxis kann das Netzwerk weiterhin ein Ergebnis ausgeben, wenn eine einzigartige Matrix während des Trainings oder in Bezug auf Inferenz vorgestellt wird. Diese Ausgabe ist jedoch nicht gültig oder aussagekräftig. Diese Einschränkung unterstreicht, wie wichtig es ist, dass die Schulungsdaten nach Möglichkeit aus nicht-singulären Matrizen bestehen.
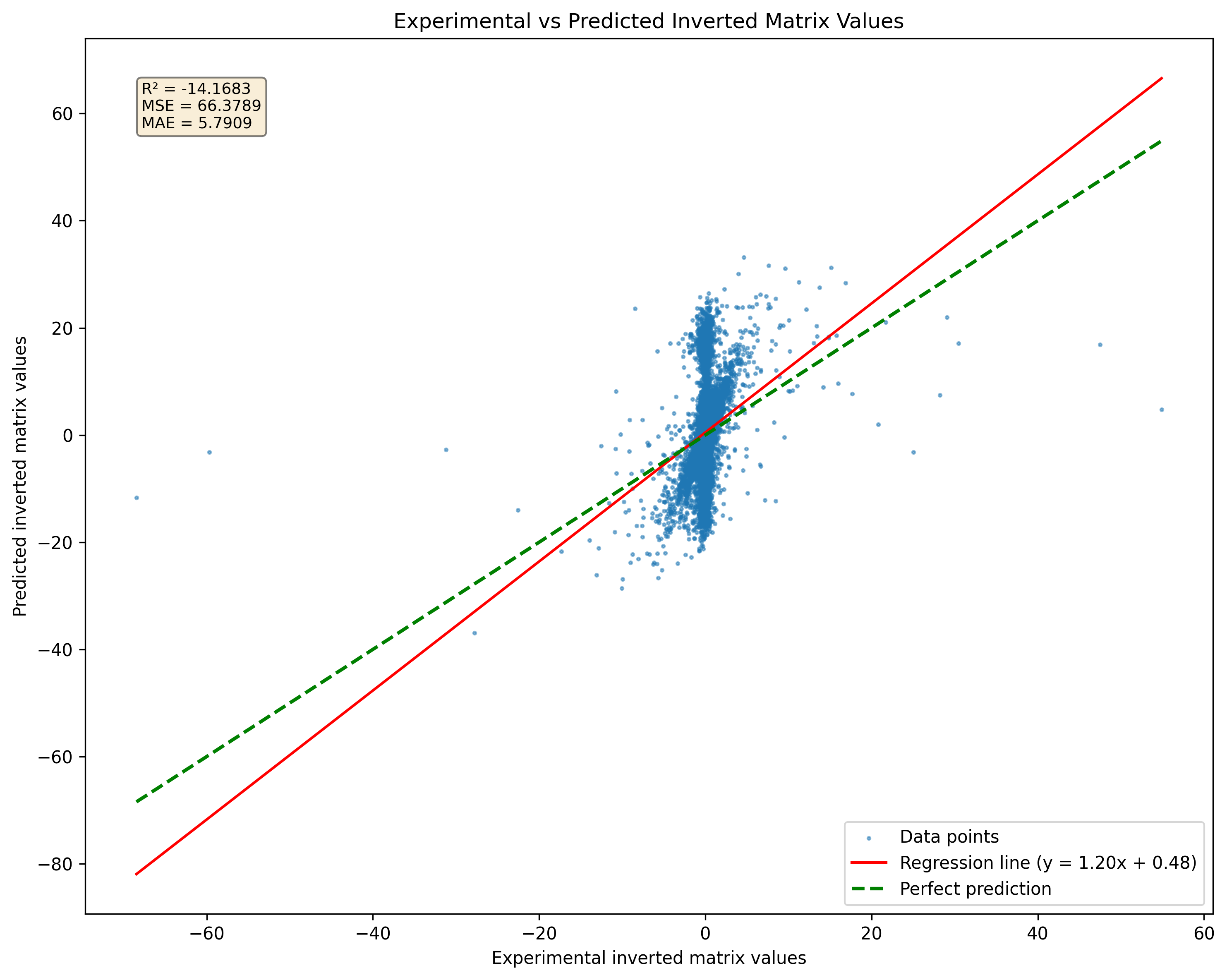Abbildung 2: Vergleich der Modellvorhersage für Singularmatrizen mit Pseudoinversionen. Beachten Sie, dass das Modell unabhängig von der Matrix -Singularität Ergebnisse erzeugt.
Untersuchungen zeigen, dass ein Resnet -Modell eine gute Anzahl von Proben ohne einen signifikanten Genauigkeitsverlust auswendig lernte. Eine Erhöhung der Datensatzgröße auf 10 Millionen Proben kann jedoch zu einer schweren Überanpassung führen. Diese Überanpassung tritt trotz des großen Datenvolumens auf, was hervorgehoben wird, dass die ledigliche Erhöhung der Datensatzgröße keine verbesserte Verallgemeinerung für komplexe Modelle garantiert. Um diese Herausforderung anzugehen, kann eine kontinuierliche Strategie zur Datenerzeugung angewendet werden. Anstatt sich auf einen statischen Datensatz zu verlassen, können Beispiele im laufenden Fliegen generiert und dem Netzwerk gespeist werden, während sie erstellt werden. Dieser Ansatz, der für die Minderung von Überanpassung von entscheidender Bedeutung ist, stellt nicht nur eine Vielzahl von Schulungsbeispielen, sondern stellt auch sicher, dass das Modell einem sich ständig weiterentwickelnden Datensatz ausgesetzt ist.
Zusammenfassend lässt sich sagen, dass die Matrix -Inversion aufgrund von Einschränkungen bei arithmetischen Operationen von Natur aus für neuronale Netze eine Herausforderung darstellt. Durch die Nutzung fortschrittlicher Architekturen wie ResNet können bessere Ergebnisse erzielt werden. Die Datenanforderungen und die Überanpassungsrisiken müssen jedoch sorgfältige Überlegungen berücksichtigt werden. Durch kontinuierliches Generieren von Trainingsmuster kann der Lernprozess des Modells und die Leistung bei Matrixinversionsaufgaben verbessert werden. Diese Version behält einen unpersönlichen Ton bei und diskutiert die Herausforderungen und Strategien bei der Ausbildung neuronaler Netzwerke für die Matrixinversion.
DeepMatrixinversion wird unter LGPLV3 -Lizenz verteilt
Um weitere Informationen zu erfahren, wie die Lizenzarbeiten funktionieren
DeepMatrixinversion ist derzeit Eigentum von Giuseppe Marco Randazzo.
Um das DeepMatrixInversion -Repository zu installieren, können Sie die Verwendung von Poesie, PIP oder PIPX unten auswählen, die die Anweisungen für beide Methoden finden.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Dadurch wird Ihre Umgebung mit allen erforderlichen Paketen eingerichtet, um DeepMatrixinversion auszuführen.
Erstellen Sie eine virtuelle Umgebung und installieren Sie Deppmatrixinversion mit PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Wenn Sie PIPX bevorzugen, sodass Sie Python -Anwendungen in isolierten Umgebungen installieren können, befolgen Sie die folgenden Schritte:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
PIPX Installieren Sie GIT+https: //github.com/gmrandazzo/deepmatrixinversion.git
Um ein Modell zu trainieren, das die Matrixinversion durchführen kann, verwenden Sie den Befehl dmxTrain. Mit diesem Befehl können Sie verschiedene Parameter angeben, die den Trainingsprozess steuern, z. B. die Größe der Matrizen, den Wertebereich und die Trainingsdauer.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
Sobald Sie Ihr Modell trainiert haben, können Sie es verwenden, um die Matrixinversion auf neuen Eingangsmatrizen durchzuführen. Der Befehl für Inferenz ist dmxinvert, der eine Eingangsmatrix aufnimmt und seine Umkehrung ausgibt.
Warnung: Dmxinvert kann eine Matrix, die größer ist als die, mit der das Modell über die Sherman-Morrison-Woodbury-Matrix-Blockinversionsformel trainiert wird. Diese Funktion funktioniert nur mit Matrizen, deren Blockgröße ohne Erinnerung durch die Modell -Trainingsblockgröße geteilt werden kann. Die Funktion ist sehr experimentell und muss möglicherweise überarbeitet werden.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Generieren eines künstlichen Datensatzes mit Eingangsmatrix und invertierter Ausgabe wird fertig mit DMX DMXDATASETGENERATOR SCHNAGE
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Dies erzeugt 10 Matrizen der Größe 3x3 mit Zahlen in einem Bereich von -1 bis +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Anschließend kann der Datensatz mit DMXDataSeTverify validiert werden
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
Die Eingabematrixdatei sollte wie folgt formatiert werden:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Jeder Zahlenblock stellt eine separate Matrix dar, gefolgt von einem Endmarker, das das Ende dieser Matrix angibt.
