Rubik's Cube Solver für sehr große Würfel.
Löst jeden Würfel einer beliebigen Größe von 1 bis 65536. Der Code kann leicht geändert werden, um noch größere Würfel zu verarbeiten. Die primäre Einschränkung ist jedoch die Menge des Speichers auf einem System und die Zeitdauer, die zur Lösung erforderlich ist. Lösen Sie die Zeit wächst ~ n^2, was bedeutet, dass es 4-5-mal länger dauert, um einen Würfel zu lösen, der in jeder Dimension 2x größer ist.
Ein 1024 geschichteter Würfel kann in etwa 1,5 Sekunden gelöst werden. Ein 16384 geschichteter Würfel kann in etwa 20 Minuten gelöst werden.
YouTube: Lösen von 65536 Ebenen YouTube: Lösen von 32768 Schichten
Bild der Vorderseite eines 32768 Würfels
Löst die Zentren und dann die Ecken und Kanten
Die Zentren werden in 15 Stadien gelöst, in denen jede Stufe alle Teile einer bestimmten Farbe von einem Gesicht zum gewünschten Gesicht bewegt. Zum Beispiel: Eine Bühne bewegt alle grünen Stücke auf das weiße Gesicht zum grünen Gesicht. Wiederholen Sie dies für alle Farben und Gesichter.
Der Löser verwendet den hier beschriebenen Kommutator, mit dem die Mittelstücke von einem Quadranten eines Gesichts zu einem Quandranten auf einem anderen Gesicht pendeln können. Eine sehr wichtige Eigenschaft dieses Kommutators ist, dass sie modifiziert werden kann, um viele Teile gleichzeitig in einzelnen Zeile zu bewegen. Für sehr große Würfel kann dies in einer einzigen Operation Hunderte, wenn nicht Tausende von Teilen bewegen. Die durchschnittliche Anzahl der Bewegungen k = (2 * p + 5) / p, wobei P die Anzahl der Teile ist, die pro Betrieb bewegt werden können. K nähert sich schnell 2, wenn die Würfelgröße zunimmt.
Die Ecken werden unter Verwendung einer grundlegenden Brute -Kraft -Methode gelöst, um die Ecke einzustellen und dann zu rotieren, bis die Gesichter korrekt ausgerichtet waren. Will Smith kann erklären: https://www.youtube.com/watch?v=wbzkdrc9vqs
Die Kanten werden gelöst, indem alle Kanten an die vordere Gesichtsanlage bewegt werden, und dann die gewünschten Stücke von der linken Kante zur rechten Kante auszutauschen. Eine Reihe von Funktionen, sofern dies erforderlich ist, um Paritätsprobleme zu beheben oder zu verhindern.
Gesichtsrotationen sind im Wesentlichen frei. Anstatt alle Teile auf ein bestimmtes Gesicht (n^2 Teile) zu bewegen, um eine Rotation durchzuführen, ändert der Löser einfach das Koordinatensystem, mit dem es zum Lesen/Schreiben auf das Gesicht verwendet wird. Dies spart eine enorme Menge an Datenaustausch.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}Dieser Code enthält einen einfachen Bildexporteur, der verwendet wird, um jedes Gesicht in ein Bild zu rendern.
https://www.nayuki.io/page/tiny-png-output
https://github.com/nayuki/nayuki-web-veröffentlichte-code
Tiny PNG Output ist eine kleine eigenständige Bibliothek, die in C und C ++ erhältlich ist, die RGB8.8.8 Pixel benötigt und eine PNG -Datei schreibt.
Die Gesamtzahl der Bewegungen kann anhand einer einfachen Formel geschätzt werden. Angenommen, der Würfel ist ausreichend randomisiert, können wir erwarten, dass das erste Gesicht 1/6 gelöst wird, und daher müssen 5/6 der Teile bewegt werden. Das zweite Gesicht wird 1/5 gelöst und erfordert, dass 4/5 der Teile bewegt werden. Das dritte Gesicht 3/4, das vierte Gesicht 2/3, das fünfte Gesicht 1/2 und das letzte Gesicht wird vollständig gelöst. Die durchschnittliche Anzahl der Bewegungen (k), um ein Stück zu bewegen, kann experimentell als ~ 2,1 geschätzt werden. Der Wert von k nimmt mit zunehmender Größe des Würfels ab. Der Wert kann niemals weniger als 2 betragen, da der Kommutator für jedes Stück mindestens zweimal bewegt werden muss.
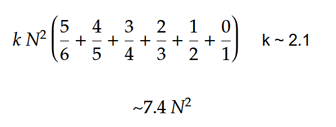
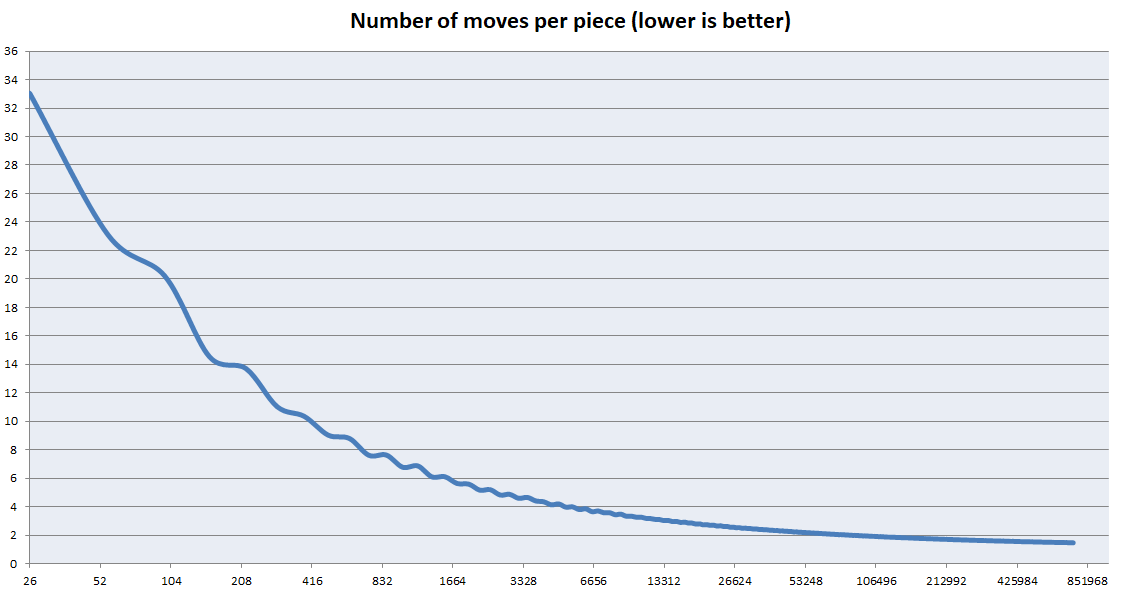
Dieser Algorithmus ist für sehr große Würfel optimiert. Es ist jedoch schrecklich für kleine Würfel. Die Hauptoptimierungen konzentrierten sich darauf, die Zentren so schnell wie möglich zu lösen, und es wurde keine Überlegung für die Lösung der Kanten gegeben. Die Größe der Kanten ist jedoch im Vergleich zu den Zentren mit zunehmender Würfelgröße unbedeutend. Die folgende Grafik zeigt, wie die durchschnittliche Anzahl der Bewegungen pro Stück mit größeren Würfeln abnimmt. Hinweis: Dies ist kein Diagramm von k. Es ist ein Diagramm von (Gesamtbewegungen) / (Anzahl der Stücke)
cmake -B build -S .
cd build
cmake --build .
RCube/RCube