Die russische Version der Aufgabe finden Sie im Repository.

Ladestufe 2…
Ladehalle…
Sie waren kürzlich in einer ähnlichen Halle. Oder war es schon lange her? Es ist schwer zu sagen. Alles ist durcheinander gebracht. Noch einmal können Sie Stimmen aus der hinteren Ecke der Halle hören. Es bedeutet, dass Sie nicht wieder allein sind. Heute ist die Halle hell beleuchtet und in perfekter Reihenfolge. Abwechslung ist gut.
Plötzlich hören Sie eine klare, perfekt hörbare Stimme von den Lautsprechern:
Hallo.
Lassen Sie mich mich vorstellen. Ich bin das kontemplative und analysierende Modul M-53. Aus unbekannten Gründen habe ich mich in dieser ziemlich langweiligen Halle befand. Es ist eine ziemlich große Verantwortung und so, aber hier gibt es nichts zu betrachten.
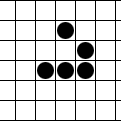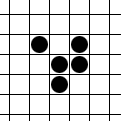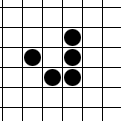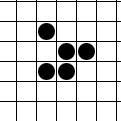
Als ich entwickelt wurde, lernte ich unter anderem aus einem bestimmten unterhaltsamen Artikel. Die Papierkopie befindet sich in der Box A1B18. Ja, genau hier. Ich habe eine kleine Anfrage für Sie: Entwickeln Sie das Spiel des Lebens aus dem Artikel; Hoffentlich wird es mich ein wenig unterhalten. Und in Frieden gehen. Die Grafiken können super einfach sein: Ich bin sehr aufgeschlossen. Pseudo-Graphics im Terminal werden in Ordnung sein. Es wäre großartig, wenn es möglich wäre, einen Zustand mithilfe einer Matrix zu initialisieren und nachzudenken. Es ist auch eine gute Idee, mindestens 5 ursprüngliche Initialisierungen mit Zuständen aus dem klassischen Set vorzubereiten (stabile Figuren, Methuselahs, periodische Zahlen, bewegliche Zahlen, Waffen, Kugelzüge, Esser, Reflektoren, Züchter usw.).
Ich freue mich darauf zu sehen, was Sie sich einfallen lassen!
Danke schön.
== Quest erhalten. Entwickeln Sie ein SRC/Game_of_Life.c -Programm in C - Eine Visualisierung des Lebensspiels. Verwenden Sie zur Anzeige der Grafiken nur ASCII -Zeichen (mit Ausgabe an das Terminal). Sie müssen eine interaktive Version des Game of Life implementieren. Erstellen Sie auch die Option zum Anpassen der Geschwindigkeit des "Spiels". ==
Behandeln Sie das Spielfeld - ein Rechteck von 80 mal 25 Zellen - als eine Matrix des Zustands des "Spiels". Es wird angenommen, dass das Feld "für sich selbst geschlossen" ist, zum Beispiel im unteren rechten Quadrat, der Nachbar auf der rechten Seite ist das untere linke Quadrat und der Nachbar unten rechts. Bereitstellung für die ursprüngliche Initialisierung des "Spiels" -Sstatus über Stdin. Bereiten Sie mindestens 5 Dateien mit anfänglichen Zuständen für die schnelle Start und Initialisierung durch Eingabeumleitung vor.
Das Spiel muss in C geschrieben werden, einen strukturierten Stil haben und vom Terminal aus verlaufen;
Ihr Quellcode wird vom statischen Analysator cppcheck sowie vom Style Linter cpplint getestet.
Anweisungen zum Ausführen dieser Tests auf Ihrem Computer finden Sie im materials .
Verwenden Sie keine umständlichen Funktionen, beschränken Sie sie auf 40 Zeilen (ohne main ).
Überprüfen Sie Ihr Programm auf Speicherlecks!
Befolgen Sie bei der Entwicklung des Spiels den Prinzipien der strukturierten Programmierung von E. dijkstra.
LADEN...
Das Spiel des Lebens, auch einfach als Leben bekannt, ist ein zellulärer Automat, der 1970 vom britischen Mathematiker John Horton Conway entwickelt wurde. Es handelt sich um ein Spiel mit Null-Player, was bedeutet, dass seine Entwicklung durch den ursprünglichen Zustand bestimmt wird und keine weiteren Eingaben erfordert. Man interagiert mit dem Spiel des Lebens, indem man eine anfängliche Konfiguration erstellt und beobachtet, wie es sich weiterentwickelt. Es ist vollständig und kann einen universellen Konstruktor oder eine andere Turing -Maschine simulieren.
Das Universum des Lebensspiels ist ein unendliches, zweidimensionales orthogonales Gitter von quadratischen Zellen, von denen jeweils in einem von zwei möglichen Zuständen lebt, lebend oder tot (oder besiedelt und unpopuliert). Jede Zelle interagiert mit ihren acht Nachbarn, die die Zellen sind, die horizontal, vertikal oder diagonal benachbart sind. Zu jedem Zeitschritt treten die folgenden Übergänge auf:
Jede lebende Zelle mit weniger als zwei lebenden Nachbarn stirbt, wie durch Unterbeamte. Jede lebende Zelle mit zwei oder drei lebenden Nachbarn lebt in der nächsten Generation. Jede lebende Zelle mit mehr als drei lebenden Nachbarn stirbt, wie durch Überbevölkerung. Jede tote Zelle mit genau drei lebenden Nachbarn wird zu einer lebenden Zelle, wie durch Fortpflanzung. Diese Regeln, die das Verhalten des Automatiks mit dem wirklichen Leben vergleichen, können in Folgendes kondensiert werden:
Jede lebende Zelle mit zwei oder drei lebenden Nachbarn überlebt. Jede tote Zelle mit drei lebenden Nachbarn wird zu einer lebenden Zelle. Alle anderen lebenden Zellen sterben in der nächsten Generation. In ähnlicher Weise bleiben alle anderen toten Zellen tot. Das anfängliche Muster bildet den Samen des Systems. Die erste Generation wird erstellt, indem die obigen Regeln gleichzeitig auf jede Zelle im Samen angewendet werden. Geburten und Todesfälle treten gleichzeitig auf, und der diskrete Moment, in dem dies geschieht, wird manchmal als Zecken bezeichnet. Jede Generation ist eine reine Funktion der vorhergehenden. Die Regeln werden weiterhin wiederholt angewendet, um weitere Generationen zu erstellen.
Ende 1940 definierte John von Neumann das Leben als eine Schöpfung (als Wesen oder Organismus), die sich selbst reproduzieren und eine Turing -Maschine simulieren kann. Von Neumann dachte über eine technische Lösung nach, die elektromagnetische Komponenten verwenden würde, die zufällig in Flüssigkeit oder Gas schweben. Dies stellte sich heraus, dass die zu dieser Zeit verfügbare Technologie nicht realistisch war. Stanislaw Ulam erfand die Mobilfunk -Automaten, die von Neumanns theoretischen elektromagnetischen Konstruktionen simulieren sollten. Ulam diskutierte mit Computern, um seine mobile Automata in einem zweidimensionalen Gitter in mehreren Papieren zu simulieren. Parallel dazu versuchte von Neumann, Ulams zellulärem Automat zu konstruieren. Obwohl er erfolgreich war, war er mit anderen Projekten beschäftigt und ließ einige Details unvollendet. Sein Bau war kompliziert, weil es versuchte, sein eigenes technisches Design zu simulieren. Im Laufe der Zeit wurden einfachere Lebenskonstruktionen von anderen Forschern bereitgestellt und in Papieren und Büchern veröffentlicht.
Motiviert durch Fragen in der mathematischen Logik und zum Teil durch Arbeiten an Simulationsspielen von Ulam, unter anderem, begann John Conway 1968 Experimente mit einer Vielzahl verschiedener zweidimensionaler Zellautomaton-Regeln. Das ursprüngliche Ziel von Conway bestand darin, eine interessante und unvorhersehbare Zelle zu definieren Automat. Zum Beispiel wollte er, dass einige Konfigurationen lange dauern, bis das Sterben und andere Konfigurationen für immer weitergehen, ohne Zyklen zuzulassen. Es war eine bedeutende Herausforderung und ein offenes Problem seit Jahren, bevor Experten für Cellular Automata beweisen konnten, dass das Lebensspiel des Lebens einer Konfiguration zugelassen wurde, die im Sinne der Befriedigung von Neumanns beiden allgemeinen Anforderungen lebte. Während die Definitionen vor dem Spiel des Lebens mit Prooden orientiert waren, zielte Conways Konstruktion auf Einfachheit ab, ohne dass ein Priori Beweis dafür lieferte, dass der Automat am Leben war.
Conway wählte seine Regeln nach beträchtlichem Experimentieren sorgfältig aus, um diese Kriterien zu erfüllen:
Es sollte kein explosives Wachstum geben. Es sollten kleine anfängliche Muster mit chaotischen, unvorhersehbaren Ergebnissen existieren. Von Neumann Universal Constructors sollte Potenzial geben. Die Regeln sollten so einfach wie möglich sein, während sie sich an die oben genannten Einschränkungen halten. Das Spiel trat in der Ausgabe von Scientific American in der Oktober 1970 in der Spalte "Mathematical Games" von Martin Gardner zu. Theoretisch hat das Spiel des Lebens die Kraft einer universellen Turing -Maschine: Alles, was algorithmisch berechnet werden kann, kann im Spiel des Lebens berechnet werden. Gardner schrieb: "Aufgrund der Analogien des Lebens mit dem Aufstieg, dem Fall und den Veränderungen einer Gesellschaft lebender Organismen gehört es zu einer wachsenden Klasse von sogenannten" Simulationsspielen "(Spiele, die realen Prozessen ähneln)."
Seit seiner Veröffentlichung hat das Spiel des Lebens aufgrund der überraschenden Möglichkeiten, wie sich die Muster entwickeln können, großes Interesse geweckt. Es bietet ein Beispiel für Entstehung und Selbstorganisation. Wissenschaftler in verschiedenen Bereichen wie Informatik, Physik, Biologie, Biochemie, Wirtschaft, Mathematik, Philosophie und generative Wissenschaften haben die Art und Weise verwendet, wie komplexe Muster aus der Implementierung der einfachen Regeln des Spiels hervorgehen können. Das Spiel kann auch als didaktische Analogie dienen, mit der die etwas kontraintuitive Vorstellung vermittelt wird, dass Design und Organisation in Ermangelung eines Designers spontan entstehen können. Zum Beispiel hat der kognitive Wissenschaftler Daniel Dennett die Analogie des Spiels des Lebens "Universum" ausführlich verwendet, um die mögliche Entwicklung komplexer philosophischer Konstrukte wie Bewusstsein und freier Wille aus den relativ einfachen Satz deterministischer physischer Gesetze zu veranschaulichen, die unsere regieren könnten Universum.
Die Popularität des Lebensspiels wurde durch die gleiche Zeit wie immer kostengünstigerer Computerzugang unterstützt. Das Spiel könnte stundenlang auf diesen Maschinen ausgeführt werden, was sonst nachts ungenutzt geblieben wäre. In dieser Hinsicht machte es die spätere Popularität computergenerierter Fraktale an. Für viele war das Spiel des Lebens einfach eine Programmierherausforderung: eine unterhaltsame Möglichkeit, ansonsten verschwendete CPU -Zyklen zu verwenden. Für einige hatte das Spiel des Lebens jedoch mehr philosophische Konnotationen. Es entwickelte einen Kult, der in den 1970er Jahren und darüber hinaus folgt; Aktuelle Entwicklungen sind so weit gegangen, um theoretische Emulationen von Computersystemen innerhalb der Grenzen eines Spiels der Lebensdauer zu schaffen.
LADEN...