Practical series of introduction to computing with engineer Mollo.

Exercises 1,2,3,4. Generate the table of arithmetic operations of n... terms:
Public Function SelectTable(n As Double , operatorString As String ) As String
Dim result, symbol As String
Dim index As Integer
Dim res As Double
result = "" : symbol = ""
For index = 0 To 10
Select Case operatorString
Case "*"
symbol = " *"
res = (index * n)
Case "/"
symbol = " /"
res = (index / n)
Case "+"
symbol = " +"
res = (index + n)
Case "-"
symbol = " -"
res = (index - n)
End Select
result = result + Str(index) + symbol + Str(n) + " = " + Str(res) + Chr( 13 ) + Chr( 10 )
Next
Return result
End Function # Output: SelectTable(TextBox1.Text, "+")
0 + 5 = 5
1 + 5 = 6
2 + 5 = 7
3 + 5 = 8
4 + 5 = 9
5 + 5 = 10
6 + 5 = 11
7 + 5 = 12
8 + 5 = 13
9 + 5 = 14
10 + 5 = 15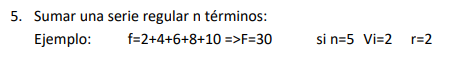
Add a regular series of n terms:
Public Function RegularSerie(n As UInt16, initialValue As Single , razon As Single , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As UInt32
Dim t, total As Single
For index = 1 To n
t = initialValue + (index - 1 ) * razon
If sumTotal Then
total += t
result = Str(total)
Else
If index = n Then
result += Str(t)
Else
result = result + Str(t) + " + "
End If
End If
Next
Return "F = " + result
End Function # Output: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 30
# Output string: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 2 + 4 + 6 + 8 + 10
F = (ln(10)+1)/1.7 + (ln(100)+2)/1.9... The Log10 argument is multiplying. X10, X10,..use multiplier accumulator.
Public Function LogarithmSerie(n As Integer , initialValue As Double , razon As Double , arg As Double , sumTotal As Boolean ) As String
Dim result As String = ""
Dim count As Double
Dim index As Integer
Dim t, f, total As Double
count = arg
t = initialValue
For index = 1 To n
If sumTotal Then
f = (Math.Log10(count) + index) / t
total += f
result = Str(total)
Else
If index.Equals(n) Then
result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t)
Else
result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t) + "+ "
End If
End If
count *= 10
t = Math.Round(t + razon, 2 )
Next
Return "F = " + result
End Function # Output: LogarithmSerie(TextBox1.Text, vi, r, arg, True)
F = 13.617137472838102
# Output string: LogarithmSerie(TextBox1.Text, vi, r, arg, False)
F = (ln(10)+1)/1.7 + (ln(100)+ 2)/ 1.9 + (ln(1000)+3)/2.1 + (ln(10000)+4)/2.3 + (ln(100000)+5)/2.5
F = 100/1 + 99/2 + 97/4... the numerator reduces the term by 1, 2, 3... while the denominator increases by 1,2,3..., it must have the initial value of the numerator VIN= 100, and initial value of the denominator VID=1.
Public Function IncreaseAndDecrease(n As Integer , initialValueNumerator As Integer , initialValueDenominator As Integer , isSumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim f, total As Double
For index = 1 To n
If isSumTotal Then
f = (initialValueNumerator / initialValueDenominator)
total += f
result = Str(total)
Else
If index = n Then
result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator)
Else
result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator) + " + "
End If
End If
initialValueNumerator -= index
initialValueDenominator += index
Next
Return "F =" + result
End Function # Output: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 195.3603896103896
# Output string: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 100/ 1 + 99/ 2 + 97/ 4 + 94/ 7 + 90/ 11
F = 5.25/0!+0 + 5.24/1!+1 + 5.22/2!+2... Both elements are regular series and for the denominator you only have to call the factorial function, of course you must learn to do the algorithm to the exam.
Public Function Factorial(number As Double ) As Double
Dim fac As Double
Dim index As Integer
If number <> 0 Then
fac = 1
For index = Math.Abs(number) To 1 Step - 1
fac *= index
Next
If number < 0 Then
fac = -fac
End If
Else
fac = 1
End If
Return fac
End Function
Public Function RegularSerieWithFactorial(n As Integer , initialValueNum As Double , initialValueDen As Double , sumTotal As Double ) As String
Dim result As String = ""
Dim index As Integer
Dim t, f, total As Double
For index = 0 To n
If sumTotal Then
If initialValueDen = 0 Then
f = 0
Else
f = initialValueNum / (Factorial(initialValueDen) + initialValueDen)
End If
total += f
result = Str(total)
Else
t = index + 1
If index = n Then
result = result + Str(Math.Round(initialValueNum, 2 )) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ")"
Else
result = result + Str(Math.Round(initialValueNum, 2 )) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ") + "
End If
End If
initialValueNum -= (t / 100 )
initialValueDen += 1
Next
Return "F = " + result
End Function # Output: RegularSerieWithFactorial(TextBox1.Text, vi, r, True)
F = 4.750333333333333
# Output string: RegularSerieWithFactorial(TextBox1.Text, vi, r, False)
F = 5.25/( ! 0+0) + 5.24/( ! 1+1) + 5.22/( ! 2+2) + 5.19/( ! 3+3) + 5.15/( ! 4+4) + 5.1/( ! 5+5)
F = X^2/2! + X^4/4! + X^6/6!+… X, is just an input variable that must be taken in the term
Public Function SumFactorial(n As Integer , x As Single , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim formule As Double
If n = 0 Then
result = Str( 0 )
End If
For index = 1 To n
If sumTotal Then
formule = Math.Pow(x, index * 2 ) / Factorial(index * 2 )
result = Str(formule)
Else
If index = n Then
result = result + "(" + Str(x) + "^" + Str(index * 2 ) + ")/" + Str(index * 2 ) + "!"
Else
result = result + "(" + Str(x) + "^" + Str(index * 2 ) + ")/" + Str(index * 2 ) + "! + "
End If
End If
Next
Return "F = " + result
End Function # Output: SumFactorial(TextBox1.Text, TextBox2.Text, True)
F = 0.0002821869488536155
# Output string: SumFactorial(TextBox1.Text, TextBox2.Text, False)
F = (2^2)/ 2 ! + (2^4)/ 4 ! + (2^6)/ 6 ! + (2^8)/ 8 ! + (2^10)/ 10 ! 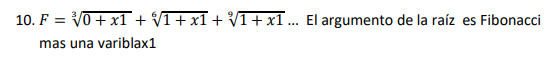
3√(0+x1) + 6√(1+x1) + 9√(1+x1)... The root argument is Fibonacci plus a variable x1.
Public Function SerieProgresiveFibonacci(n As Integer , x As Double , viRoot As Integer , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index, a, b, c, root As Integer
Dim formule, total As Double
a = - 1 : b = 1 : root = viRoot
For index = 1 To n
c = a + b
If sumTotal Then
formule = (c + x) ^ ( 1 / root)
total += formule
result = Str(total)
Else
If index = n Then
result = result + Str(index * 3 ) + "√(" + Str(c) + "+" + Str(x) + ")"
Else
result = result + Str(index * 3 ) + "√(" + Str(c) + "+" + Str(x) + ") + "
End If
End If
a = b
b = c
root *= 3
Next
Return "F = " + result
End Function # Output: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 5.455187736786854
# Output string: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 3√(0+2) + 6√(1+2) + 9√(1+2) + 12√(2+2) + 15√(3+2)
20√cos(0.2) - 19√cos(0.4) + 18√cos(0.6)... “pimponea”, that is, add the term and subtract, add and subtract. THIS IS NOT N TERMS, BUT UNTIL THE ROOT IS 2, SO THE LAST ELEMENT WILL BE 2√cos(...).
Public Shared Function Pinponear(root As Double , vi As Double , razon As Double , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim count, total, formule As Double
count = vi
For index = root To 2 Step - 1
If sumTotal Then
If index Mod 2 <> 0 Then
formule = -Math.Pow(Math.Cos(count), 1 / index)
Else
formule = Math.Pow(Math.Cos(count), 1 / index)
End If
total += formule
result = Str(total)
Else
If index = 2 Then
result = result + Str(index) + "√cos(" + Str(count) + ")"
Else
If index Mod 2 <> 0 Then
result = result + Str(index) + "√cos(" + Str(count) + ") + "
Else
result = result + Str(index) + "√cos(" + Str(count) + ") - "
End If
End If
End If
count = Math.Round(count + razon, 2 )
Next
Return "F = " + result
End Function # Output: Pinponear(TextBox1.Text, vi, r, True)
F = 5.455187736786854
# Output string: Pinponear(TextBox1.Text, vi, r, False)
F = 3√(0+2) + 6√(1+2) + 9√(1+2) + 12√(2+2) + 15√(3+2)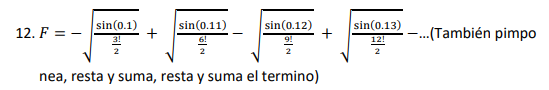
√(sin(0.1)/(3!/2)) + √(sin(0.11)/(3!/2))... It also pings, subtracts and adds, subtracts and adds the term.
Public Function ProgresiveSeriePinponear(n As Integer , initValue As Double , r As Double , arg As Double , sumTotal As Boolean )
Dim result As String = ""
Dim index As Integer
Dim total, formule, count As Double
count = initValue
For index = 1 To n
If sumTotal Then
formule = Math.Sqrt(Math.Sin(arg) / (Factorial(count) / 2 ))
total = -total + formule
result = Str(total)
Else
If index Mod 2 = 0 Then
result = result + "+ √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
Else
result = result + "- √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
End If
End If
arg = Math.Round(arg + r, 2 )
count += 3
Next
Return "F = " + result
End Function # Output: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, True)
F = -0.16574853902978934
# Output string: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, False)
F = - √sin( 0.1)/( 3 ! /2) + √sin( 0.11)/( 6 ! /2) - √sin( 0.12)/( 9 ! /2) + √sin( 0.13)/( 12 ! /2)
(π/2)/√(1000+0) + (π/1.9)/√(1001+1) + (π/1.8)/√(1003+1) The argument of the root increases in a progression: From 1st to 2nd 1; from 2nd to 3rd 2; from the 3rd to the 4th 3; …while the other is Fibonacci.
Public Function ProgresiveSerieFibonacci(n As Integer , initValue As Integer , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim count, a, b, c, total, formule As Double
count = 2 : a = - 1 : b = 1
For index = 1 To n
c = a + b
If sumTotal Then
formule = ( 3.14159 / count) / Math.Sqrt(initValue + c)
total += formule
result = Str(total)
Else
If index = n Then
result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ")"
Else
result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ") + "
End If
End If
a = b
b = c
count = Math.Round(count - 0.1 , 2 )
initValue += index
Next
Return "F = " + result
End Function # Output: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, True)
F = 0.27688777750129406
# Output string: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, False)
F = (π/ 2)/√( 1000+ 0) + (π/ 1.9)/√( 1001+ 1) + (π/ 1.8)/√( 1003+ 1) + (π/ 1.7)/√( 1006+ 2) + (π/ 1.6)/√( 1010+ 3)
2√x^2/100 + 4√x^4/50 + 8√x^8/25... The root multiplies, while the denominator within the root unfolds (divides).
Public Function SerieMultiplyAndUnfold(n As Integer , root As Double , num As Double , denom As Double , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim total, formule As Double
For index = 1 To n
If sumTotal Then
formule = Math.Pow(Math.Pow(num, root) / denom, 1 / root)
total += formule
result = Str(total)
Else
If index = n Then
result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ")"
Else
result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ") + "
End If
End If
root = Math.Round(root * 2 , 2 )
denom = Math.Round(denom / 2 , 2 )
Next
Return "F = " + result
End Function # Output: SerieMultiplyAndUnfold(TextBox1.Text, TextBox2.Text,TextBox3.Text, TextBox4.Text, True)
F = 1.9987716171427177
# Output string with params: SerieMultiplyAndUnfold(4, 2, 1, 100, False)
F = 2√( 1^ 2/ 100) + 4√( 1^ 4/ 50) + 8√( 1^ 8/ 25) + 16√( 1^ 16/ 12.5)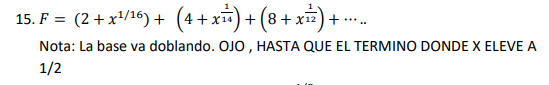
( 2+x^(1/16)) + (4+x^(1/14))... The base is doubling. BE CAREFUL, UNTIL THE TERM WHERE X RAISES TO 1/2
Public Function SerieBaseIsDoubling(n As Integer , base As Double , x As Double , denom As Double , sumTotal As Boolean ) As String
Dim result As String = ""
Dim index As Integer
Dim total, formule As Double
For index = 1 To n
If sumTotal Then
formule = base + Math.Pow(x, 1 / denom)
total += formule
result = total
Else
If denom >= 2 Then
If index = n Then
result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))"
Else
result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + ")) + "
End If
End If
End If
base *= 2
denom -= 2
Next
Return "F = " + result
End Function # Output: SerieBaseIsDoubling(TextBox1.Text, vi, r, arg, True)
F = 2056
# Output string with params: SerieBaseIsDoubling(10, 2, 1, 16, False)
F = ( 2+ 1^(1/ 16)) + ( 4+ 1^(1/ 14)) + ( 8+ 1^(1/ 12)) + ( 16+ 1^(1/ 10)) + ( 32+ 1^(1/ 8)) + ( 64+ 1^(1/ 6)) + ( 128+ 1^(1/ 4)) + ( 256+ 1^(1/ 2))