Greedy Gaussian Segmentation (GGS) es un solucionador de Python para segmentar eficientemente datos de series temporales multivariadas. Para obtener detalles sobre la implementación, consulte nuestro documento en http://stanford.edu/~boyd/papers/ggs.html.
El GGS Solver toma una matriz de datos n por T y divide las T marcas de tiempo en un vector de n dimensiones en segmentos sobre los cuales los datos se explican bien como muestras independientes de una distribución gaussiana multivariada. Lo hace formulando un problema de máxima verosimilitud regularizado por covarianza y resolviéndolo utilizando una heurística codiciosa, cuyos detalles completos se describen en el artículo.
git clone [email protected]:davidhallac/GGS.git
cd GGS
python helloworld.py
ggs.py esté en el mismo directorio que su nuevo archivo y luego agregue el siguiente código al comienzo de su script: from ggs import *
El paquete GGS tiene tres funciones principales:
bps, objectives = GGS(data, Kmax, lamb)
Encuentra K puntos de interrupción en los datos para un parámetro de regularización determinado lambda
Entradas
datos: una matriz de datos n por T, con T marcas de tiempo de un vector de n dimensiones
Kmax: el número de puntos de interrupción a encontrar
lamb - parámetro de regularización para la covarianza regularizada
Devoluciones
bps: Lista de listas, donde el elemento i de la lista más grande es el conjunto de puntos de interrupción que se encuentran en K = i en el algoritmo GGS
objetivos: lista de los valores objetivos en cada paso intermedio (para K = 0 a Kmax)
meancovs = GGSMeanCov(data, breakpoints, lamb)
Encuentra las medias y covarianzas regularizadas de cada segmento, dado un conjunto de puntos de interrupción.
Entradas
datos: una matriz de datos n por T, con T marcas de tiempo de un vector de n dimensiones
puntos de interrupción: una lista de ubicaciones de puntos de interrupción
lamb - parámetro de regularización para la covarianza regularizada
Devoluciones
meancovs: una lista de tuplas (media, covarianza) para cada segmento de los datos
cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])
Ejecuta una validación cruzada 10 veces y devuelve la probabilidad del conjunto de prueba y tren para cada par (K, lambda) hasta Kmax.
Entradas
datos: una matriz de datos n por T, con T marcas de tiempo de un vector de n dimensiones
Kmax: el número máximo de puntos de interrupción para ejecutar GGS
lambList: una lista de parámetros de regularización para probar
Devoluciones
cvResults: lista de tuplas (lamb, ([TrainLL],[TestLL])) para cada parámetro de regularización en lambList. Aquí, TrainLL y TestLL son la probabilidad logarítmica promedio por muestra en los 10 pliegues de validación cruzada para todas las K desde 0 hasta Kmax.
Parámetros opcionales adicionales (para las tres funciones anteriores):
características = [] - seleccione un determinado subconjunto de columnas en los datos para operar
verbose = False - Imprime los pasos intermedios al ejecutar el algoritmo
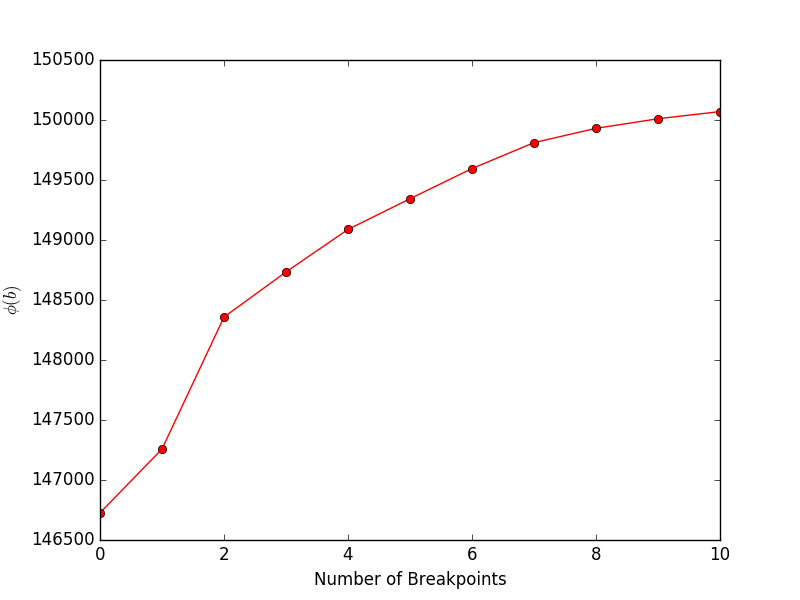
Al ejecutar financeExample.py se obtendrá el siguiente gráfico, que muestra el objetivo (Ecuación 4 en el documento) frente al número de puntos de interrupción:
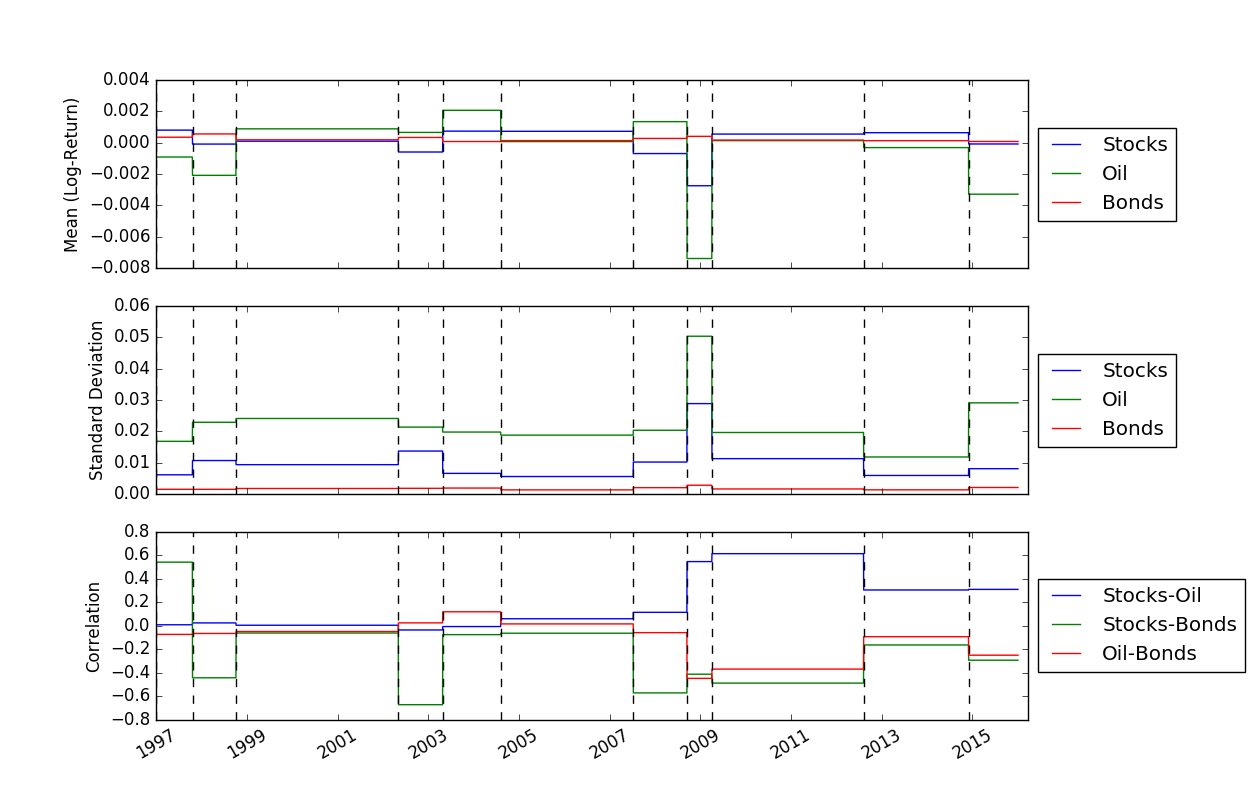
Una vez que hayamos resuelto las ubicaciones de los puntos de interrupción, podemos usar la función FindMeanCovs() para encontrar las medias y covarianzas de cada segmento. En el ejemplo de helloworld.py , al trazar las medias, varianzas y covarianzas de las tres señales se obtiene:
Para ejecutar una validación cruzada, que puede ser útil para determinar los valores óptimos de K y lambda, podemos usar el siguiente código para cargar los datos, ejecutar la validación cruzada y luego trazar la prueba y entrenar la probabilidad:
from ggs import *
import numpy as np
import matplotlib.pyplot as plt
filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]
#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)
trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()
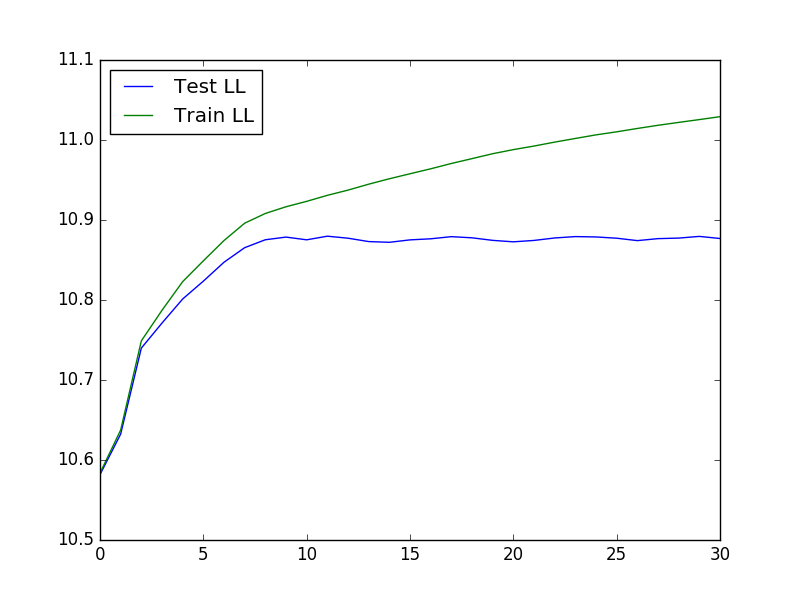
El gráfico resultante se parece a:
Segmentación gaussiana codiciosa de datos de series temporales: D. Hallac, P. Nystrup y S. Boyd
David Hallac, Peter Nystrup y Stephen Boyd.