Análisis de series temporales

Pronóstico de acciones de Tesla mediante modelos de series temporales Obteniendo la información bursátil de Tesla Company (NASDAQ: TSLA) a través de Yahoo Finance. Este proyecto aplicará los métodos de análisis de series de tiempo para investigar la información básica de TSLA y descomponer las series de tiempo de TLSA.
Los métodos de suavizado exponencial para pronosticar el precio del TSLA en los próximos 365 días, y luego utilizarán
El modelo ARIMA para predecir el precio. Este proyecto también comprobará la distribución de errores para comprobar el rendimiento del modelo.

Descomponer la serie temporal

Descomponer una serie temporal significa separarla en sus componentes constituyentes, que suelen ser un componente tendencial y un componente irregular, y si se trata de una serie temporal estacional, un componente estacional. Para la información de acciones de TSLA, en la figura del gráfico de tendencia de precios, podemos ver que no hay un componente estacional dentro de los datos. Pero estos datos de series temporales deberían incluir un componente de tendencia y un componente irregular. Descomponer la serie temporal implica intentar separar la serie temporal en estos componentes, es decir, estimar el componente tendencial y el componente irregular. Usaremos la función SMA() para suavizar los datos de TSLA. Elegiremos el orden diferente (n=8 y n=40) para comprobar el componente de tendencia. El objetivo es que intentemos suavizar los datos con una media móvil simple.

Modelo de pronóstico y evaluación: suavizado exponencial

Modelo de suavizado exponencial
El modelo de suavizado exponencial se puede utilizar para realizar pronósticos a corto plazo para datos de series de tiempo. A partir de los datos de TSLA, sabemos que puede describirse como el modelo aditivo sin estacionalidad. En el gráfico de tendencias, podemos ver que las fluctuaciones aleatorias en la serie temporal parecen tener un tamaño aproximadamente constante a lo largo del tiempo. Entonces usaremos la función HoltWinter() para ajustar una predicción de suavizado exponencial simple.

Modelo de Pronóstico y Evaluación: Modelo ARIMA

Modelo ARIMA

ARIMA (Promedio móvil integrado autorregresivo) es una herramienta importante utilizada en el análisis de series de tiempo para intentar pronosticar valores futuros de una variable en función de su valor actual. Ecuación de pronóstico ARIMA(p,d,q): Los modelos ARIMA son, en teoría, la clase más general de modelos para pronosticar una serie temporal que se puede convertir en “estacionaria” mediante diferenciación. Los modelos ARIMA están definidos para series temporales estacionarias. Por lo tanto, si comienza con una serie de tiempo no estacionaria, primero necesitará "diferenciar" la serie de tiempo hasta obtener una serie de tiempo estacionaria. Para diferenciar la serie de tiempo d veces para obtener una serie estacionaria, usamos la función diff(). Luego usaremos la Una prueba ADF formal no rechaza la hipótesis nula de no estacionariedad, confirmando nuestra inspección visual:

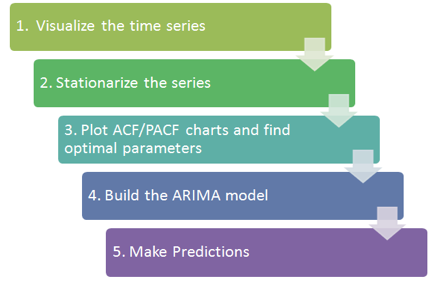
Resumen

En esta sección, utilizamos los datos de las acciones de TESLA como series de tiempo. Lo descomponemos y utilizamos el suavizado exponencial de HoltWinter y ARIMA para pronosticar el precio futuro de las acciones. Los procedimientos básicos son los que se muestran en la siguiente figura.

La otra cosa es que siempre debemos analizar los errores y ajustar los parámetros del modelo para lograr mejores resultados. resumen