smard power forecasting
1.0.0
Este repositorio es para pronosticar el consumo de energía alemán.
Basado e inspirado en:
Fuente de datos: SMARD
Coloque todos los archivos descargados en:
/example/dataset # there is already used dataset included if you pull, but you could update
Consulte el archivo Forecast.Rmd para ver cómo puede ejecutar este código en una versión actualizada de SMARD-Data.
Bibliotecas utilizadas:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
Intente trabajar en la carpeta ejemplo/para comenzar.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
Se generaron las siguientes funciones a partir del conjunto de datos y la API de vacaciones:
| Índice | Nombre de columna | Descripción |
|---|---|---|
| 1 | Fecha desde | Para validación de DateIndex (similar, pero sin formato) |
| 2 | Consumo de energía | Consumo de energía en MW |
| 3 | Índice de fechas | Marca de tiempo (aaaa-mm-dd hh:mm:ss) |
| 4 | Día laborable | Mo, Di, Mi, Do, Fr, Sa, So (días laborables en alemán) |
| 5 | Fecha | Fecha (aaaa-mm-dd) |
| 6 | Año | Año aaaa |
| 7 | Semana | Número de semana 0-53 |
| 8 | Hora | Número de hora 0-24 |
| 9 | Mes | Mes número 1-12 |
| 10 | nombre local | Nombre de un día festivo para la marca de tiempo |
| 11 | Día laboral | 1/0 Si es día laboral (Werktag), entonces 1 |
| 12 | Mes | 1/0 Si es lunes entonces 1 |
| 13 | Di | 1/0 Si es martes entonces 1 |
| 14 | Mi | 1/0 Si miércoles entonces 1 |
| 15 | Hacer | 1/0 Si es jueves entonces 1 |
| 16 | fr | 1/0 Si es viernes entonces 1 |
| 17 | sa | 1/0 Si es sábado entonces 1 |
| 18 | Entonces | 1/0 Si es domingo, entonces 1 (no es necesario, si se usa de lunes a sábado) |
| 19 | Día festivo | 1/0 Si es feriado entonces 1 |
| 20 | Día laboralVacacionesFin de semana | Si es feriado, fin de semana o día laborable (para Parcelas, es Char.) |
| 21 | día festivo y trabajo | 1/0 Si el feriado es un día laborable entonces 1 |
| 22 | El último día no fue el día del trabajo | 1/0 Si el último día no fue laborable entonces 1 |
| 23 | El último día no fue el día del trabajo y ahora el día del trabajo | 1/0 Si el último día no era un día laborable y ahora sí lo es, entonces 1 |
| 24 | El día siguiente no es el día del trabajo y ahora el día del trabajo | 1/0 Si el día siguiente no es un día laborable y ahora es un día laborable, entonces 1 |
| 25 | El último día fue festivo y no fin de semana | 1/0 Si el último día fue feriado y no fin de semana, entonces 1 |
| 26 | El día siguiente es festivo y no fin de semana | 1/0 Si el día siguiente es feriado y no fin de semana, entonces 1 |
| 27 | Nombre de vacaciones | similar a localName (Nombre del día festivo) |
| 28 | findeaño | 1/0 Si es fin de año (Semana 52 o 53) |
| 29 | Primera semana del año | 1/0 Si es inicio de año (Semana 1) |
| 30 | VacacionesExtendido | 1/0 Día festivo retrasado (6 horas después del día siguiente) |
| 31 | VacacionesSuavizado | HolidayExtend + sin(2*pi(Hora)+1)/24) |
| 32 | MediaÚltimaSemana | Consumo de energía medio de la última semana (turno: 24*8-25) |
| 33 | MediaÚltimosDosDías | Consumo de energía medio de los dos últimos días (Shift: 24*3-25) |
| 34 | MaxÚltimoDía | Max PowerConsum del último día (Shift: 24*2-25) |
| 35 | MinÚltimoDía | Consumo de energía mínimo del último día (Shift: 24*2-25) |
En este estudio hay un conjunto de datos sobre el consumo de energía en Alemania de SMARD para los años 2015 - 2024.
La Figura 1 muestra el conjunto de datos sin procesar con valores faltantes (rojo), marcas de tiempo duplicadas (rojo oscuro) y consumo de energía a lo largo del tiempo (gris), resolución horaria. Con un valor faltante y un duplicado cada año, fue fácil limpiar el conjunto de datos. En general, un conjunto casi limpio. Después de limpiar el conjunto de datos, hay observaciones plausibles sobre el consumo de energía:
Existe un enfoque simple para llenar los vacíos tomando la última observación (posible, porque la resolución es lo suficientemente grande y porque solo faltan unos pocos valores). El primer valor se mantuvo para duplicados.
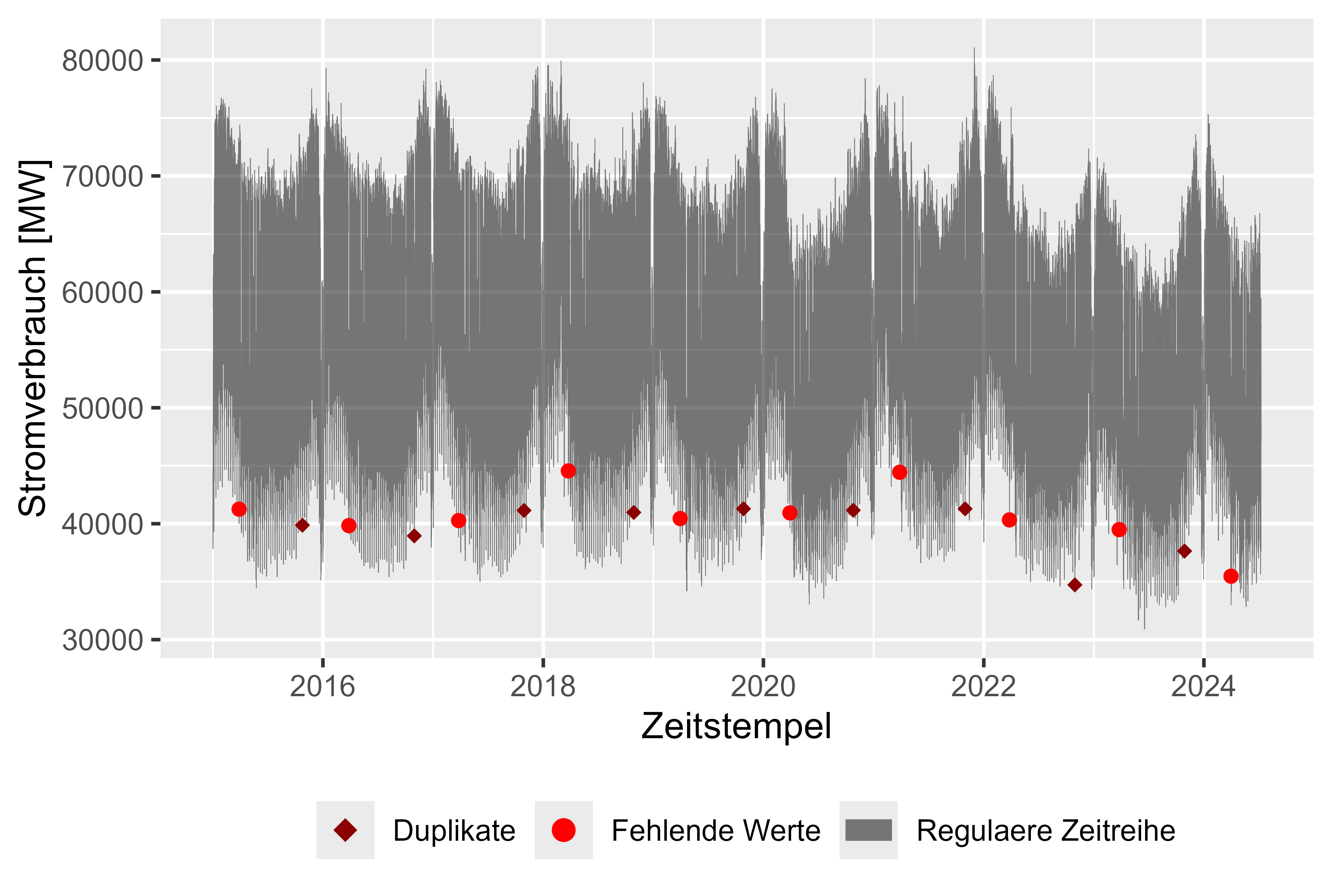Figura 1 Consumo de energía bruta
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
Las siguientes secciones entrarán cada vez más en detalle de los datos. Empezaremos aquí con la representación anual.
La Figura 2 es la representación anual de los años 2015-2024. Podemos notar aquí que a principios de año hay un aumento del consumo de energía y al final del año hay una disminución (Navidad, Año Nuevo). En general, parece una sonrisa o un lazo.
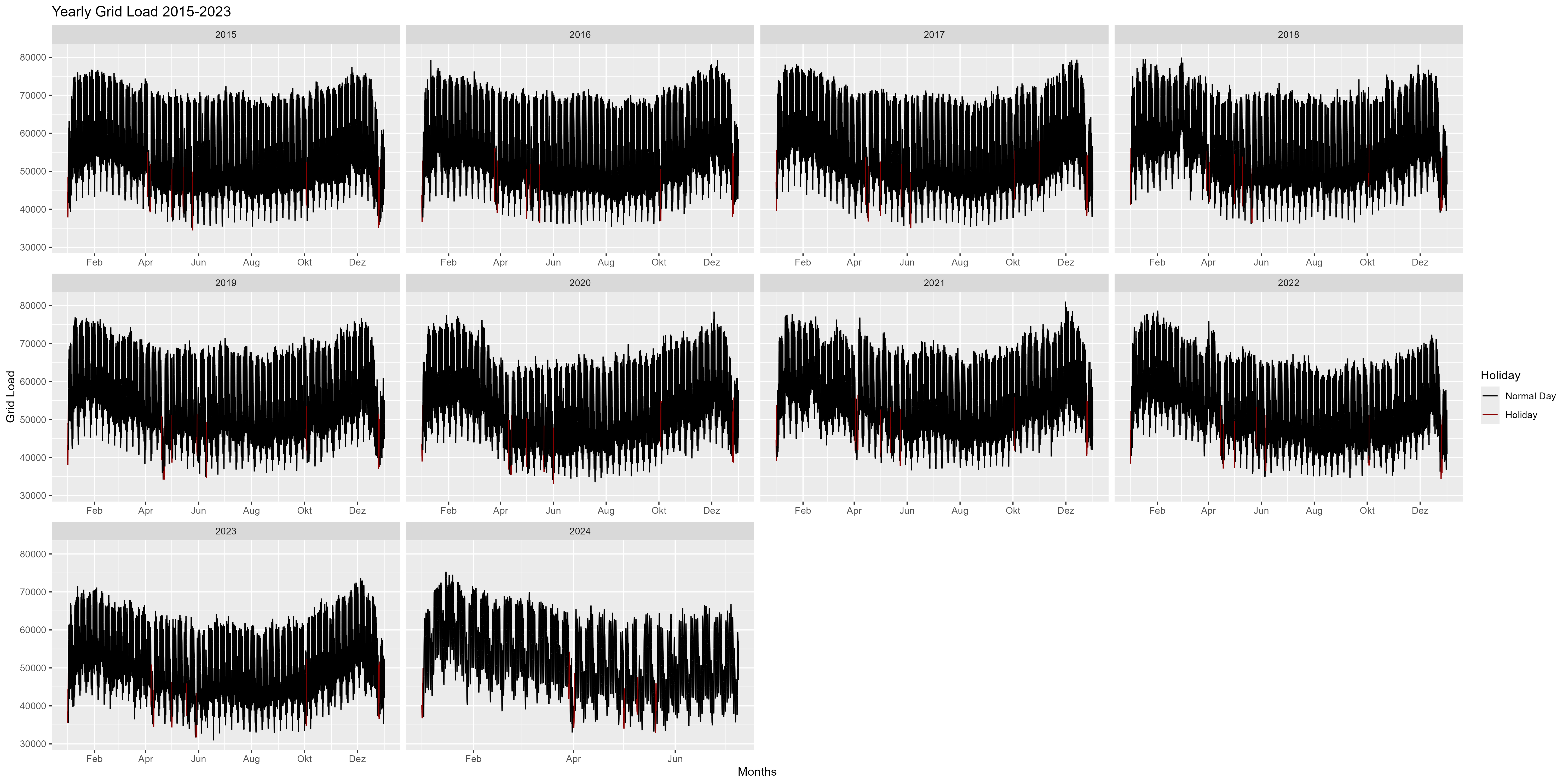Figura 2 Consumo de energía, cada año como faceta única
Intentemos agregar todos los años y dividirlos en semanas. Los diagramas de caja de la Figura 3 combinan todos los años. Podemos ver el patrón con más detalle. El principio y el final de un año se representan en rojo y muestran una disminución con respecto a la "forma de sonrisa" habitual.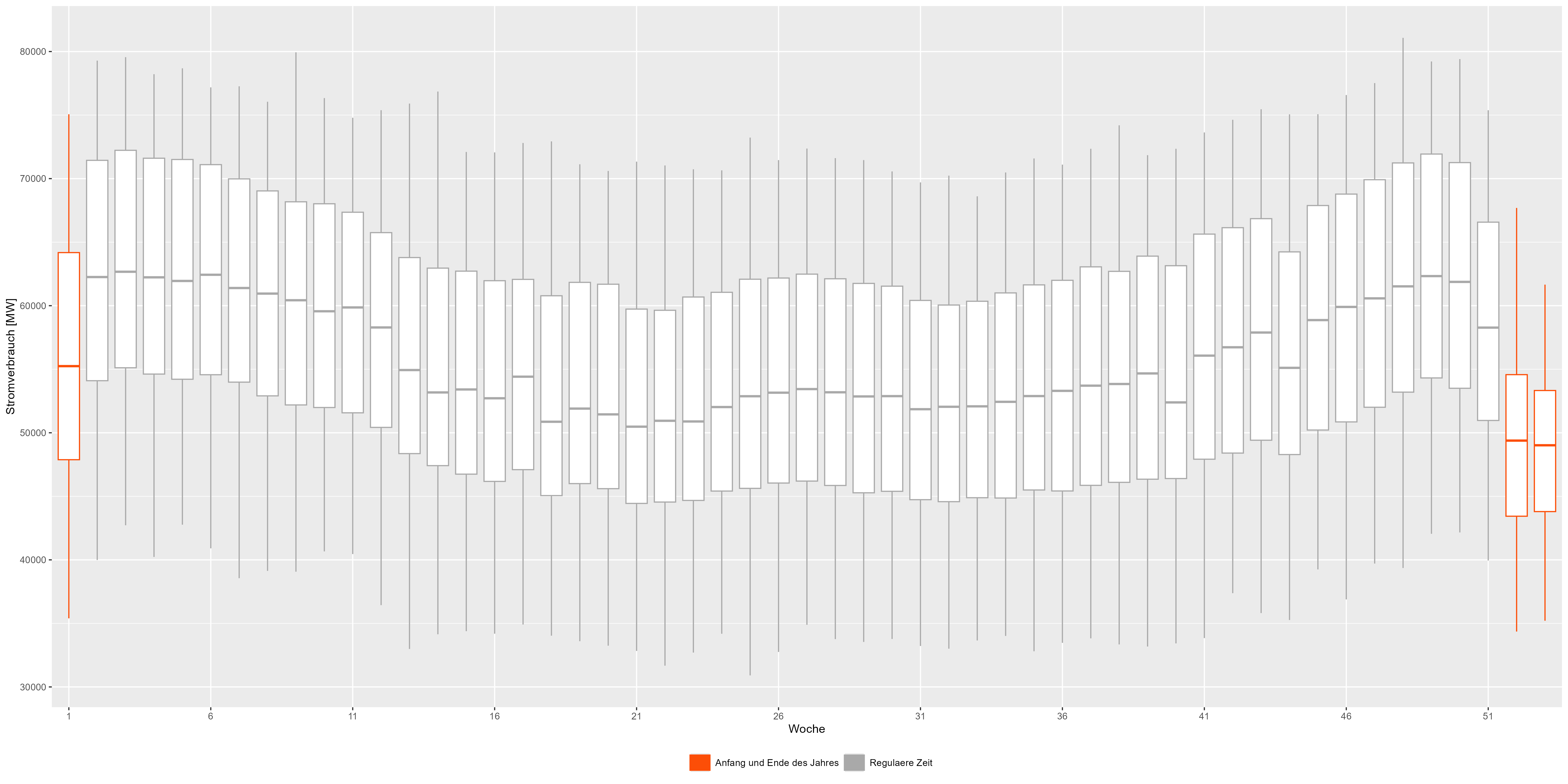
Figura 3 Datos agregados semanales del consumo de energía
Vayamos más en detalle y analicemos el año 2018, por ejemplo. La Figura 4 es la representación mensual del año 2018. Aquí podemos observar con más detalle el cierre del año. Alrededor del 24 de diciembre se produce una disminución del consumo de energía. También destacan aquí los fines de semana y festivos (rojo). Una disminución para todos los fines de semana y para todos los días festivos.
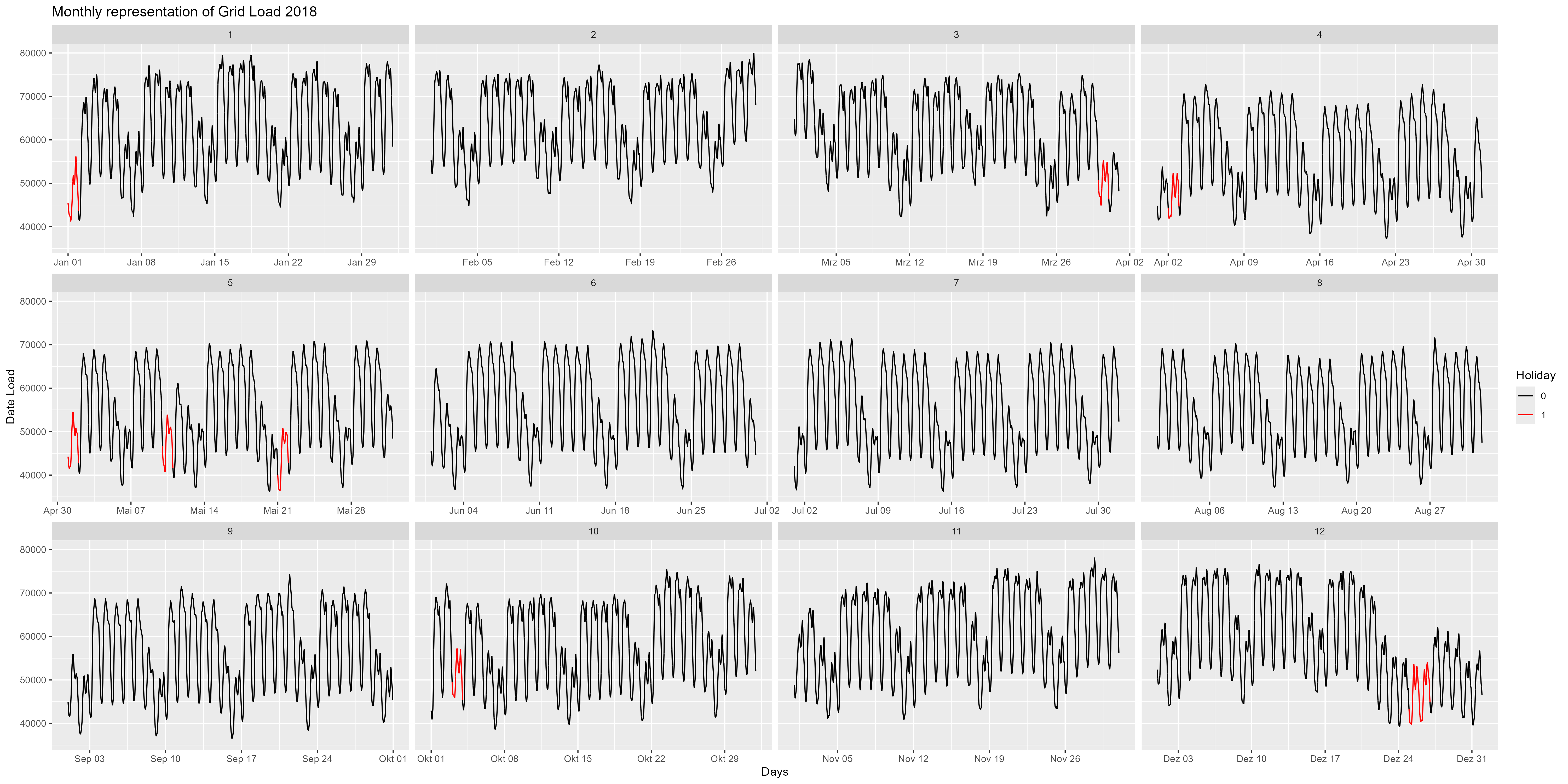Figura 4 Consumo de energía, cada mes como faceta única
Podríamos ir aún más lejos y comprobar la representación horaria de los datos. La Figura 5 muestra el diagrama de caja agregado para cada hora. También se produce un descenso del horario nocturno (21:00-06:00) y un aumento del horario diurno/laboral (06:00-21:00). También un patrón que debe incluirse en el modelo.
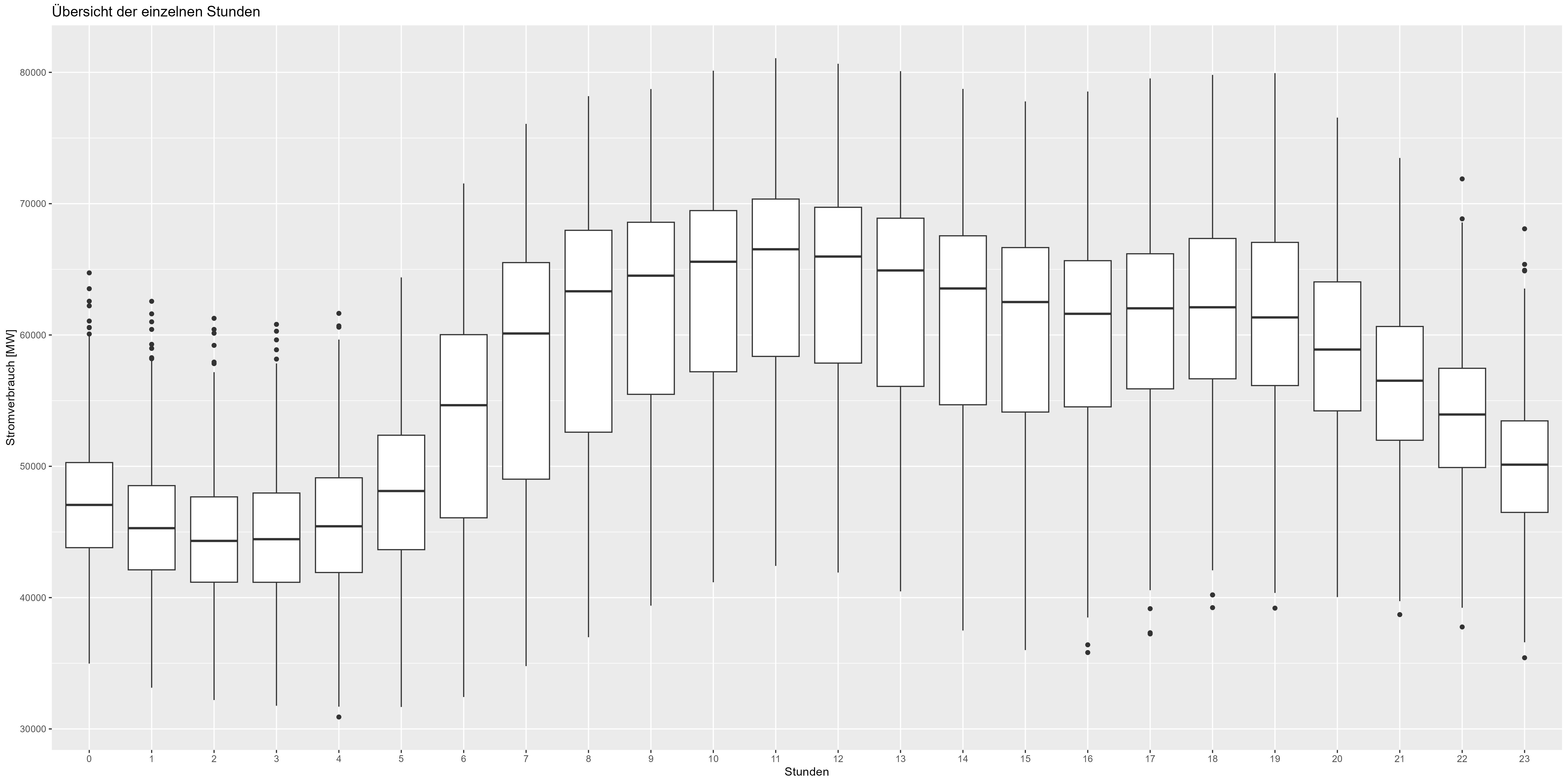Figura 5 Datos agregados por hora del consumo de energía
Hablemos de los días de semana. Como se supone, el fin de semana el consumo eléctrico disminuye. "Durchschnitt" es el término medio. La Figura 6 muestra todos los días de la semana (agregados) a lo largo de los años. Hay una disminución de ~10.000 MW para los fines de semana.
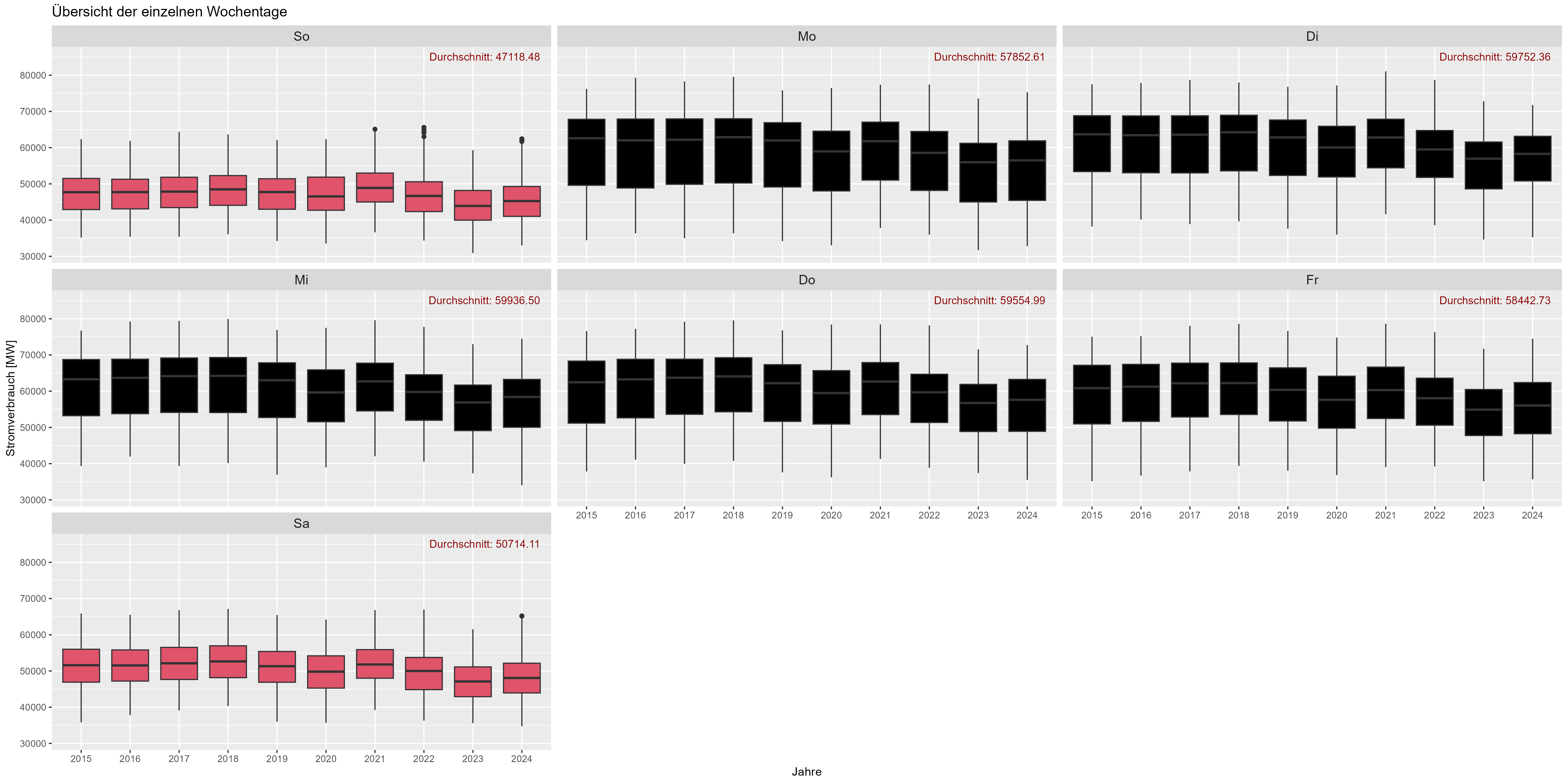Figura 6 Consumo de energía "efecto día de la semana"
La Figura 8 muestra el efecto de las vacaciones. "Durchschnitt" es el consumo medio de energía a lo largo de años. Hay un aumento significativo del consumo de energía durante los "días laborables" (gris oscuro) en comparación con los días festivos (rojo). Podríamos suponer aquí que los días festivos actúan como fines de semana para el Power-Consum".
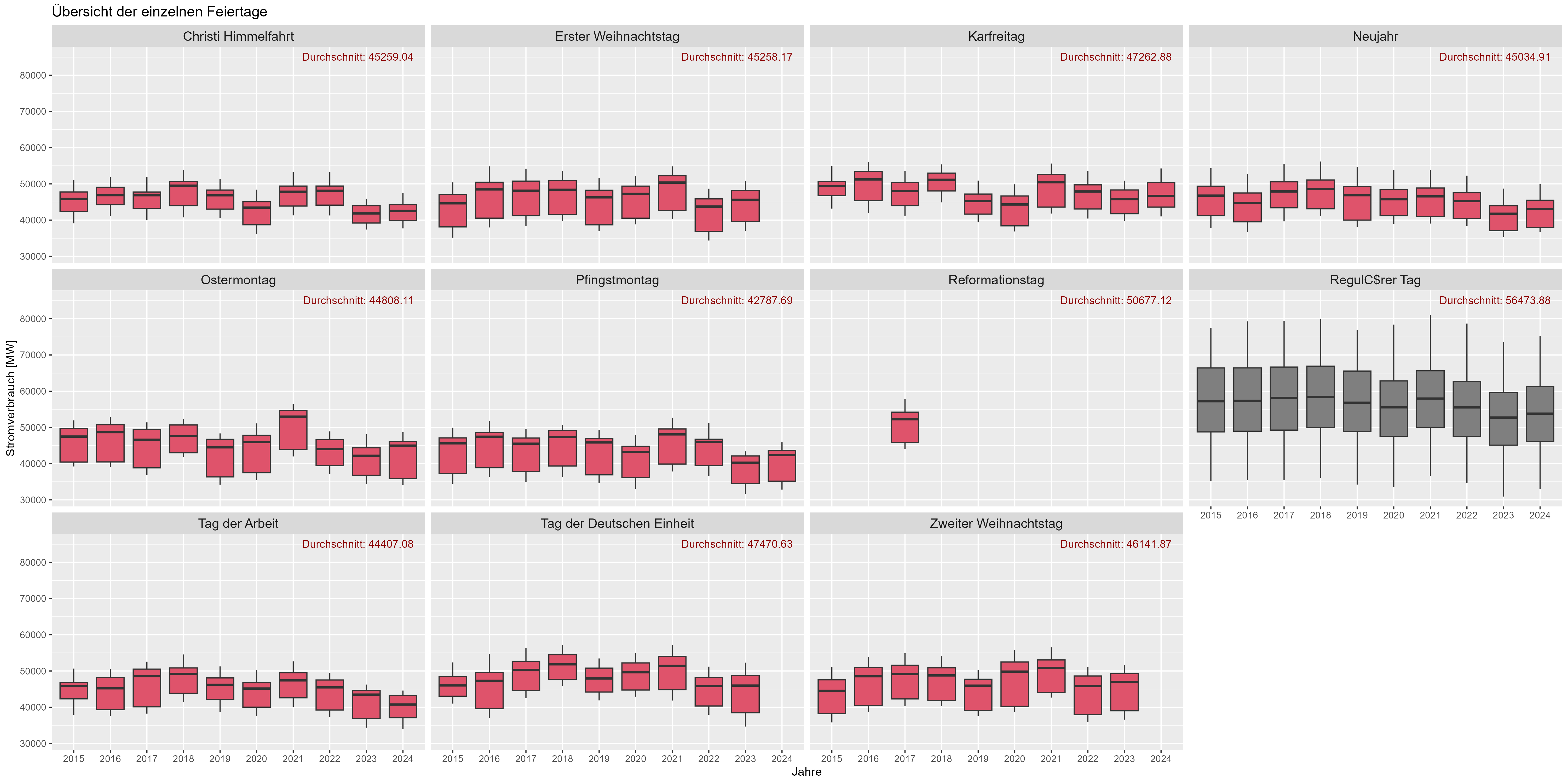Figura 6 Consumo de energía "efecto vacaciones"
La Figura 7 representa diferentes comportamientos para diferentes días. Hay 4 categorías. "Feiertag Kein Wochenende" significa que es un día festivo, pero no un fin de semana. "Feiertag Wochenende" significa día festivo y fin de semana. "Kein Feiertag Kein Wochenende" significa que es un día laboral normal y "Kein Feiertag Wochenende" significa que es sólo fin de semana. Podemos observar distribuciones similares para los días laborables no regulares como se supone.
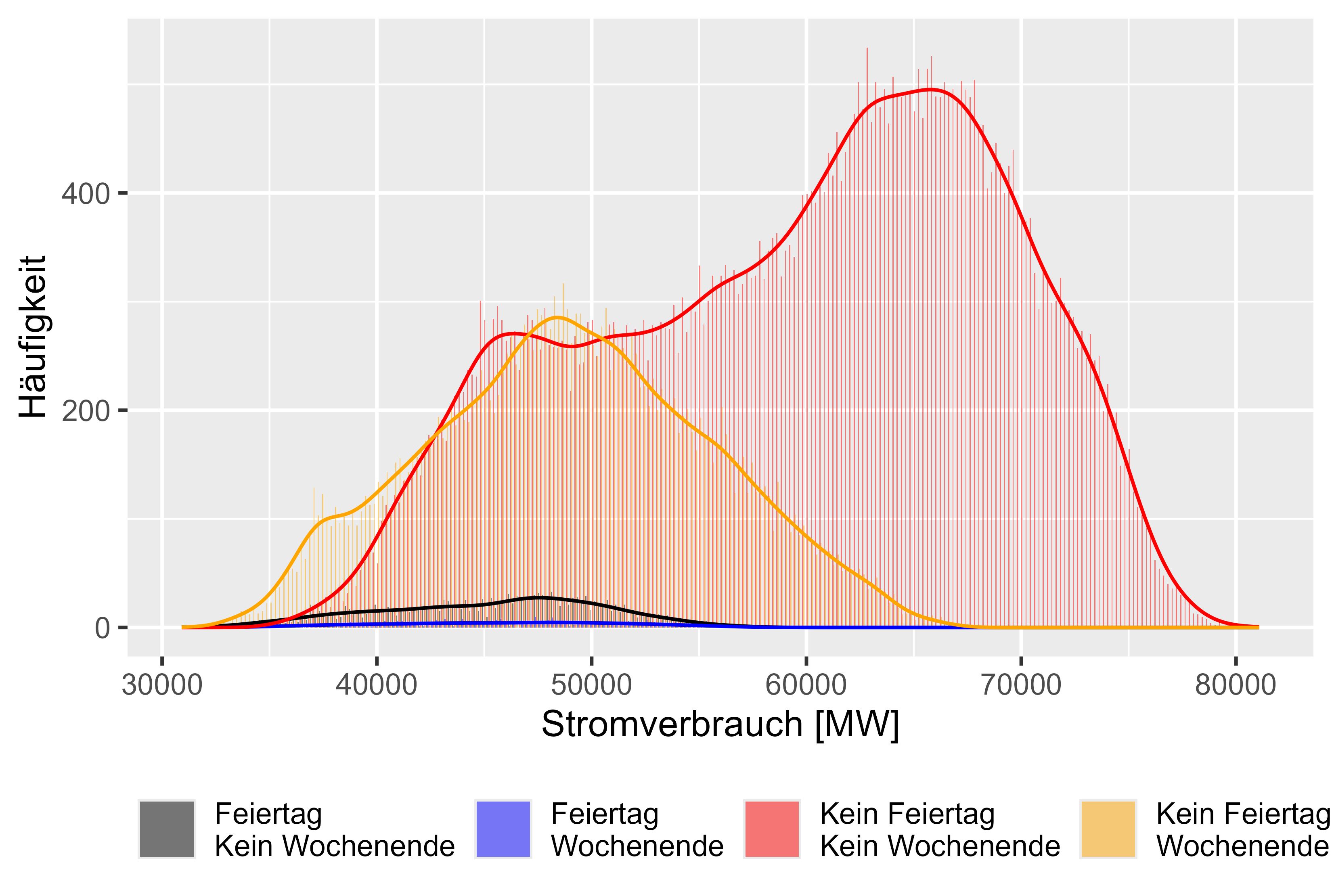Figura 7 Comparación del consumo de energía con "diferentes efectos"
Los valores rezagados como MeanLastTwoDays, MeanLastWeek, MaxLastOneDay y MinLastOneDay son funciones generadas.
Similar a lo comentado en DOI: 10.1109/TPWRS.2011.2162082 - Previsión de carga a corto plazo basada en un modelo aditivo semiparamétrico
Las figuras 8 a 11 (en rojo no son días hábiles) representan estos valores rezagados frente al consumo de energía real.
Existe una ligera correlación para estas características generadas.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| Característica | Correlación con PowerConsum |
|---|---|
| VacacionesSuavizado | -0.556194 |
| MediaÚltimaSemana | 0.389044 |
| MediaÚltimosDosDías | 0.201253 |
| MaxÚltimoDía | 0.320193 |
| MinÚltimoDía | 0,348583 |
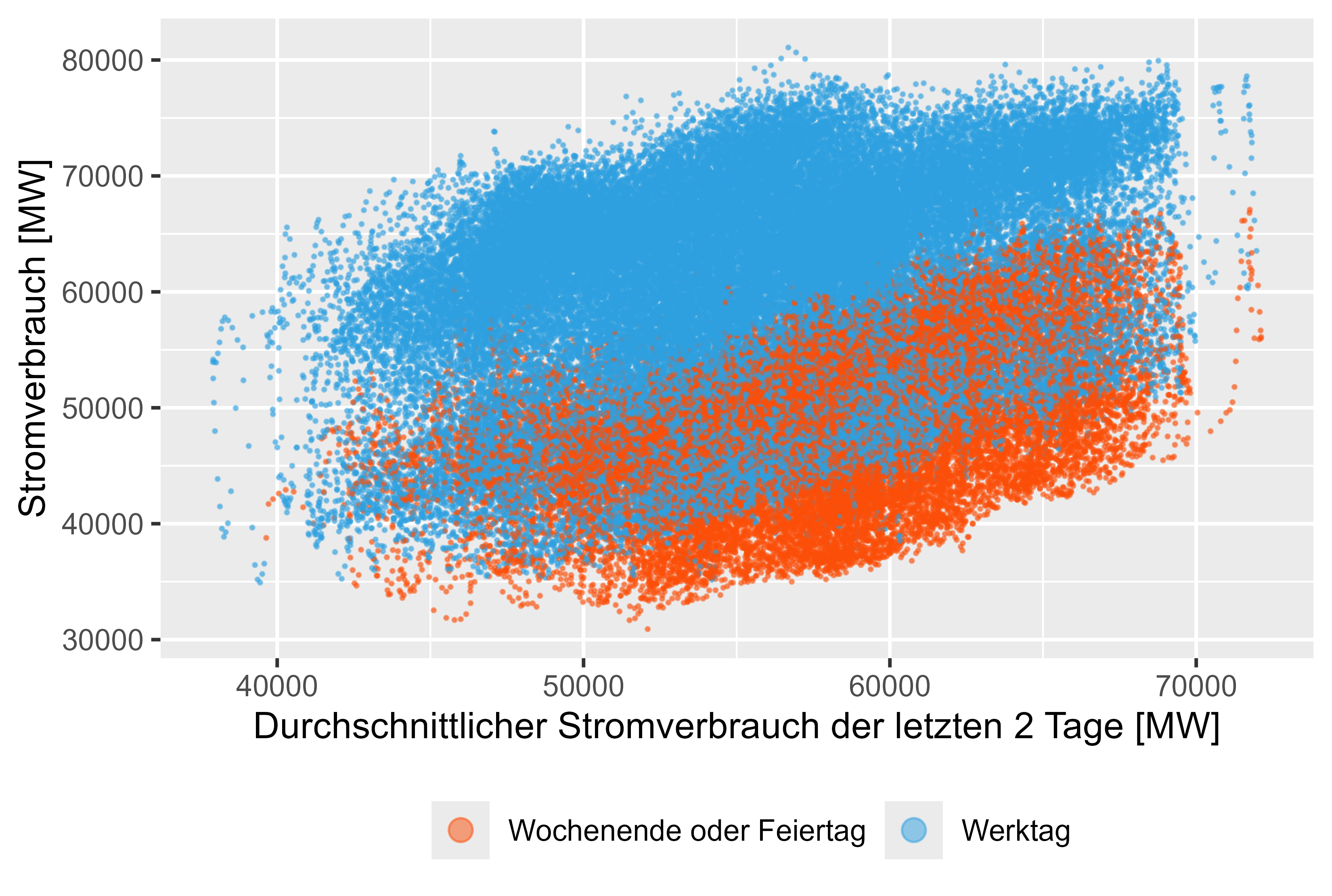Figura 8 Consumo de energía: MeanLastTwoDays
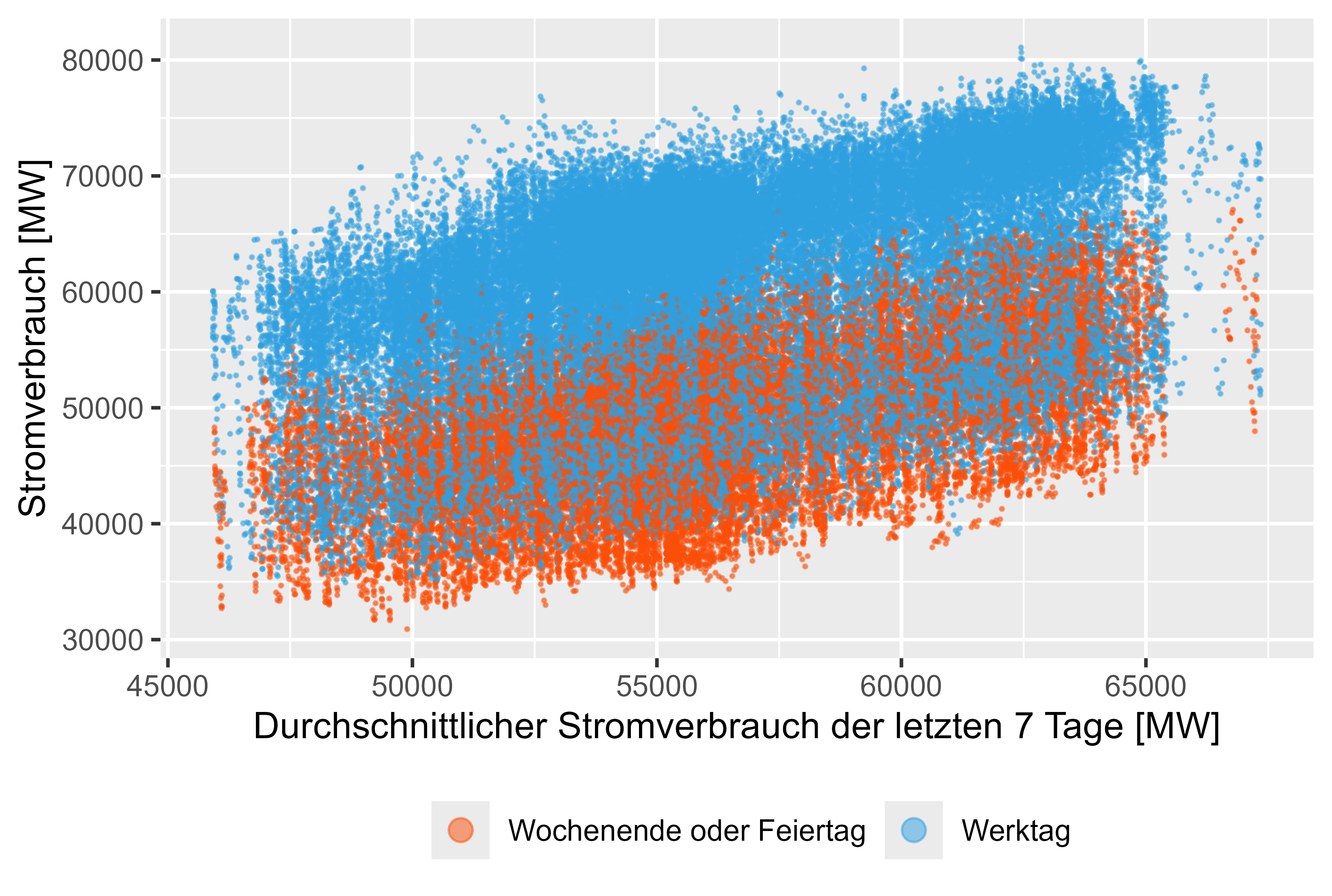Figura 9 Consumo de energía: media de la última semana
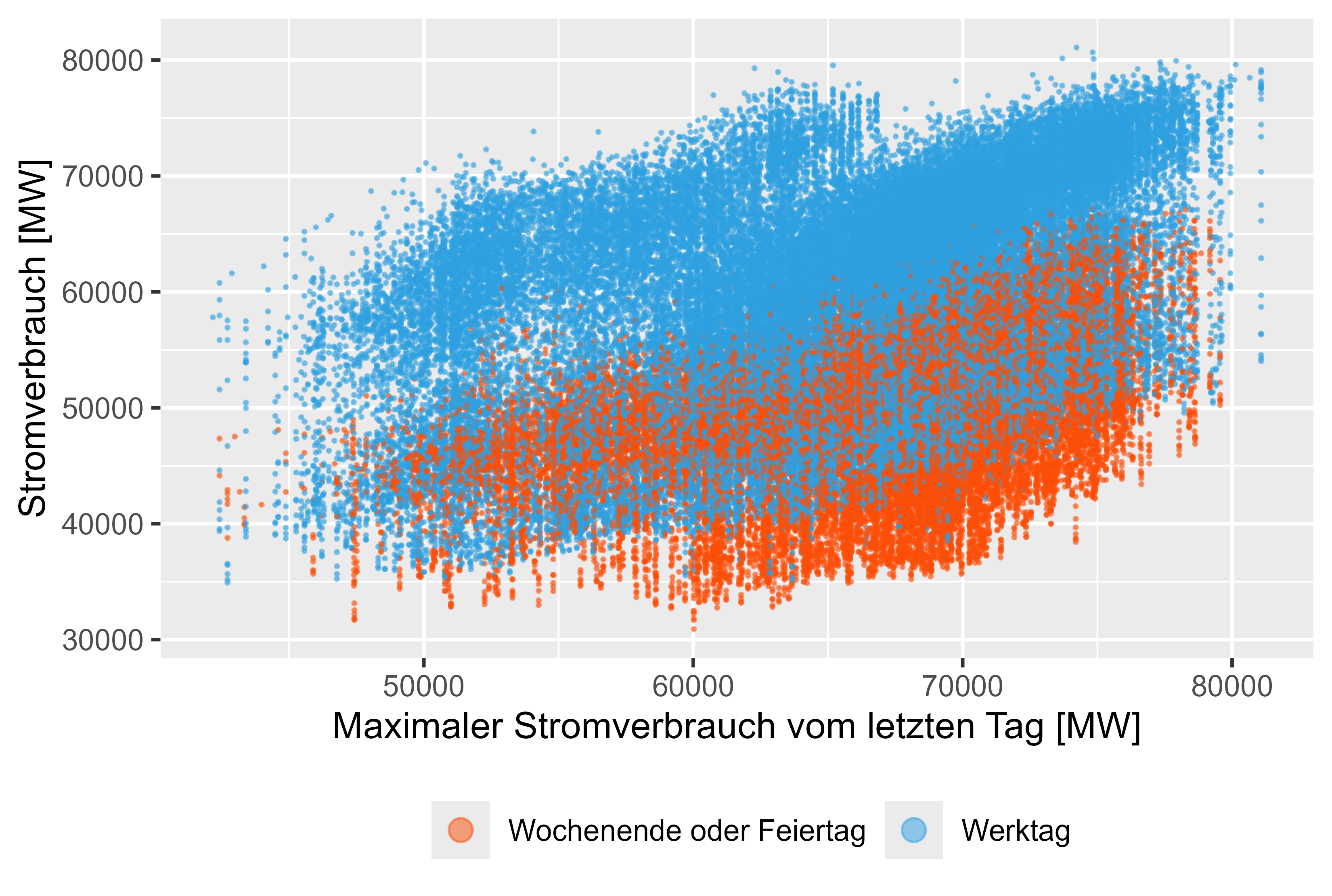Figura 10 Consumo de energía: MaxLastOneDay
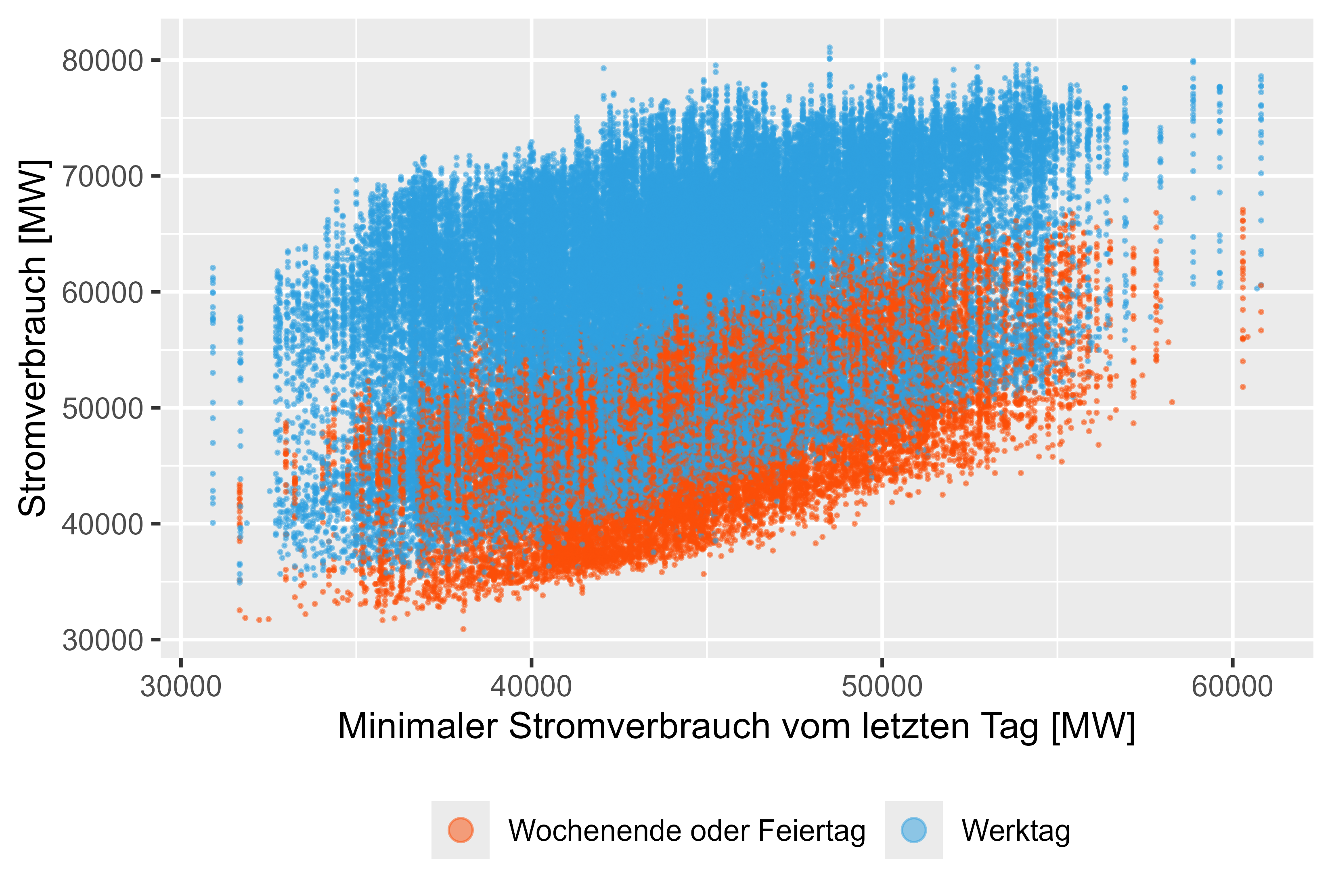Figura 11 Consumo de energía: MinLastOneDay
Hay una estacionalidad compleja. Para la resolución horaria existe una estacionalidad anual, semanal y diaria. Lo cual debe ser rastreado por el modelo. La solución aquí es la que se analiza en Pronósticos: Principios y práctica Capítulo 12.1 Estacionalidad compleja para usar términos de Fourier para representar y ensamblar mediante cos() y sin() la estacionalidad compleja.
Podemos echar un vistazo pequeño al gráfico ACF y PACF, hay algunos picos significativos, pero es solo la representación de 96 valores rezagados. Si tomamos las ~9000 observaciones retrasadas durante un año, habría una estacionalidad compleja. Por eso es más fácil optar por el término de Fourier. Tampoco funcionó bien simplemente buscando componentes PDQ y pdq por
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
sí mismo. Además, el tiempo de entrenamiento aumenta dramáticamente sin los términos de Fourier.
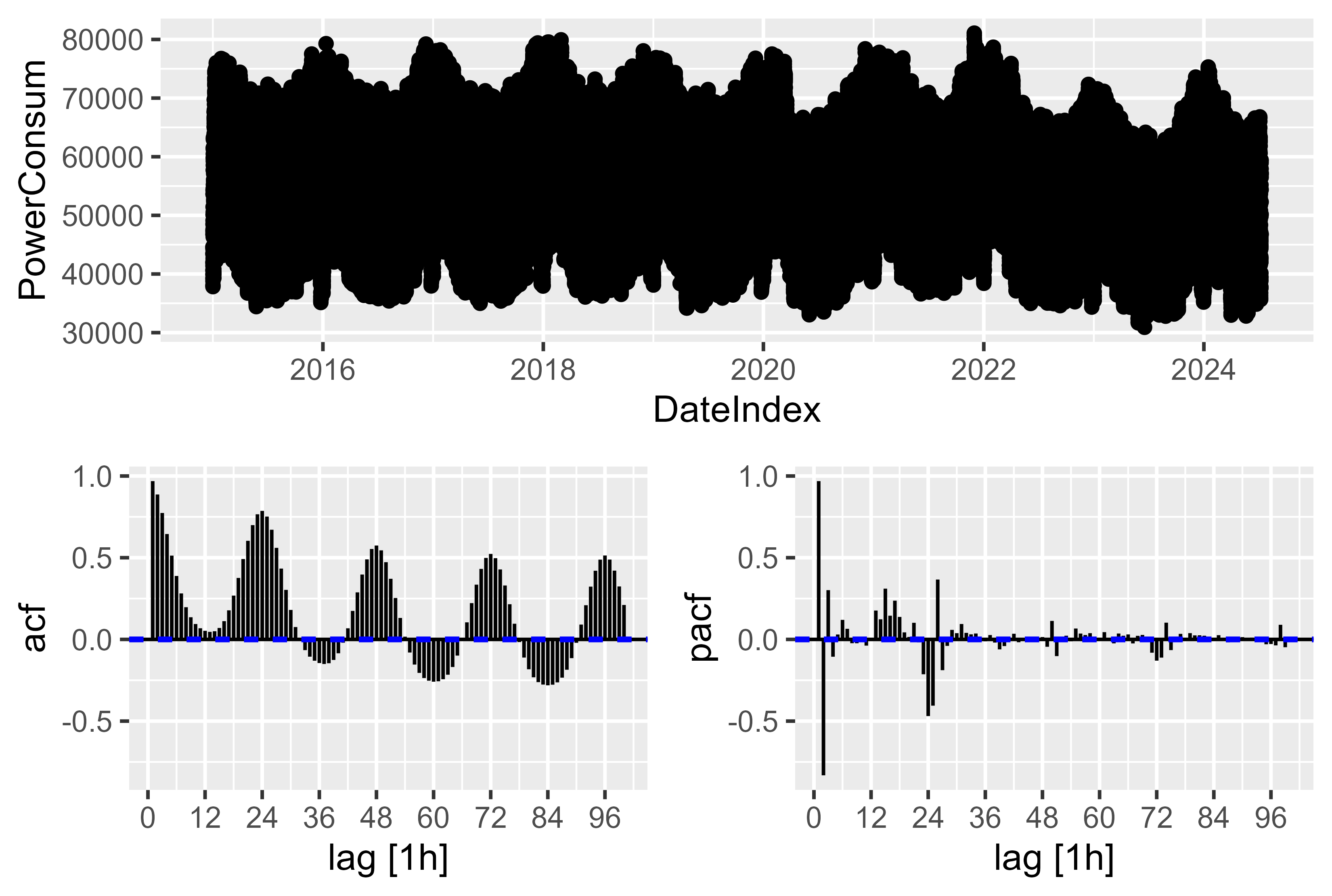Figura 12 Consumo de energía: ACF PACF Gráfico del consumo de energía bruta
La mejor combinación de características encontrada en este trabajo es:
Para comparar los modelos utilizamos las métricas MAE y MAPE. SMARD es el modelo de "Bundesnetzagentur" de la página SMARD. El modelo Prophet también se probó y tuvo un desempeño sólido, pero no lo suficientemente bueno.
Los valores previstos por SMARD alcanzaron un MAPE de 3,6%. <- NO EN ESTE ESTUDIO.
Datos de entrenamiento:
El mejor modelo encontrado hasta ahora guerra LHM + DHR (modelo armónico lineal + regresión armónica dinámica)
La idea es ensamblar un modelo lineal con el modelo ARIMA. Porque era difícil para el modelo ARIMA lidiar con variables ficticias para los días festivos. Entonces el modelo conjunto ayudó.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
Podríamos visualizar el efecto y cómo funciona el modelo. La Figura 13 muestra la idea detrás de este modelo. En primer lugar ajustamos el modelo LHM y calculamos los residuos. Entrene el modelo DHR por los residuos y resuma ambos. Es una especie de espejo en el LHM y empuja los valores hacia arriba.
Para el modelo LHM utilizamos aquí un enfoque simple: una curva sinusal que se repite cada 24 horas y disminuye o aumenta en días festivos o días laborables.
Al pronosticar LHM sobre datos nuevos, podemos pronosticar los residuos de datos nuevos. Residuales + LHM desplazan los valores de nuevo a la posición "correcta".
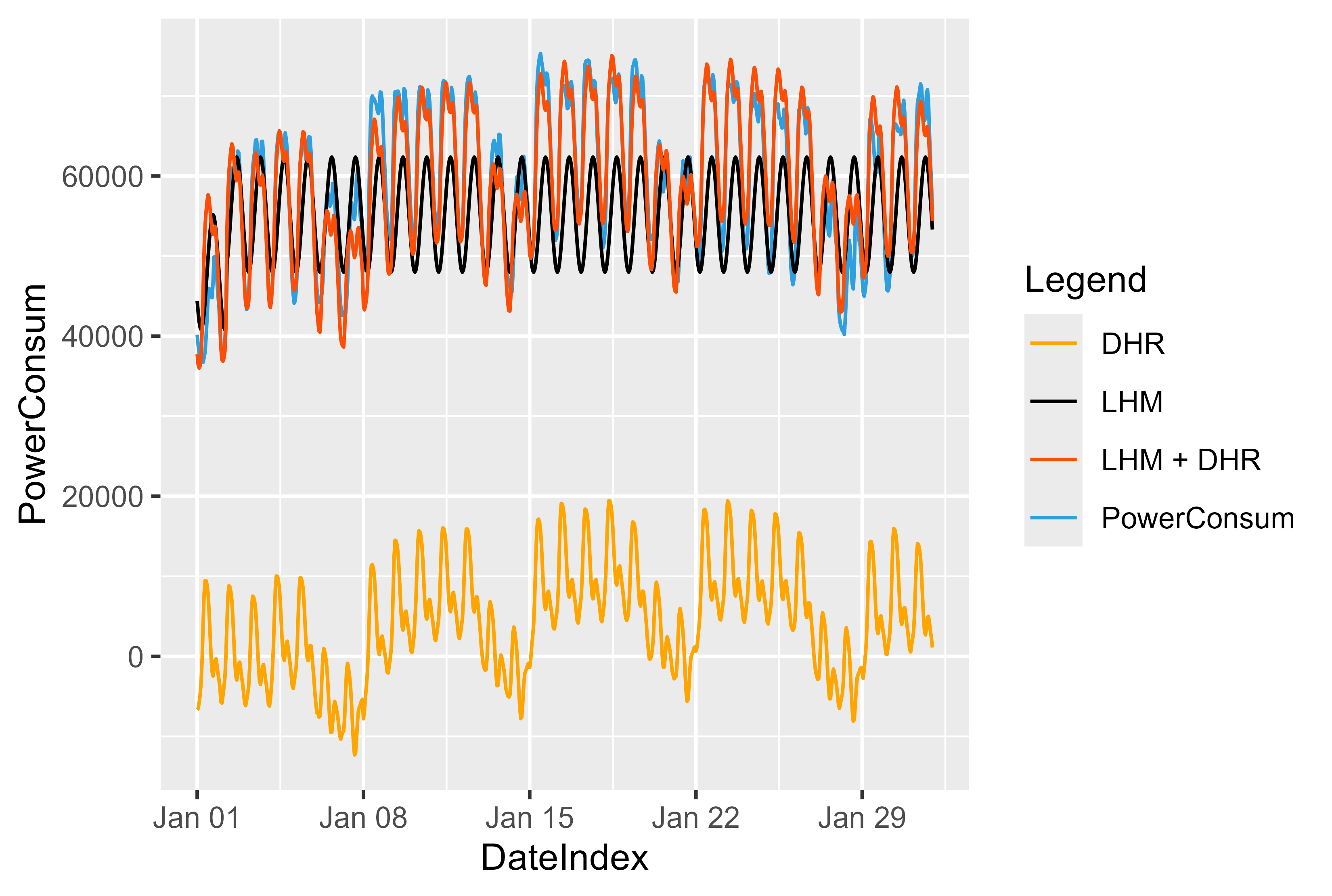Figura 13 Representación del modelo LHM + DHR
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
Una puntuación sólida de MAPE 3,8% para la versión_5 (modelo LHM + DHR).
Echemos un vistazo más profundo si usáramos solo el modelo ARIMA (arima_14). La Figura 14 representa los resultados de este modelo. Podemos ver los días festivos (naranja), fin de semana (rojo) y día normal (azul). Hay valores atípicos significativos para las vacaciones, aunque había una variable ficticia para el modelo ARIMA, no pudo captar las vacaciones correctamente.
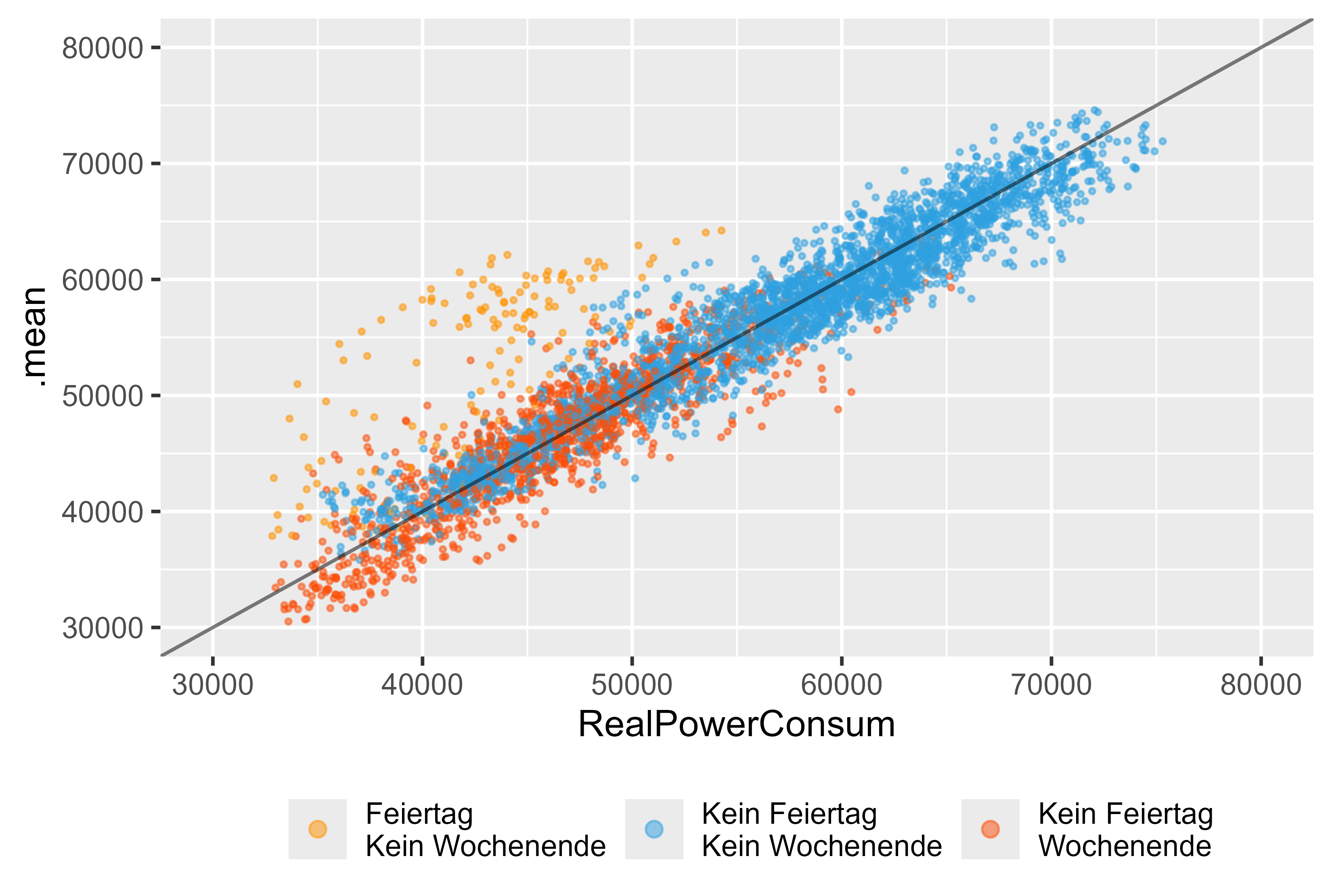Figura 14 Valores previstos frente a valores reales ARIMA (DHR, arima_14), como modelo único
Por otro lado el modelo LHM + DHR muestra un mejor desempeño para las vacaciones. La figura 15 lo representa.
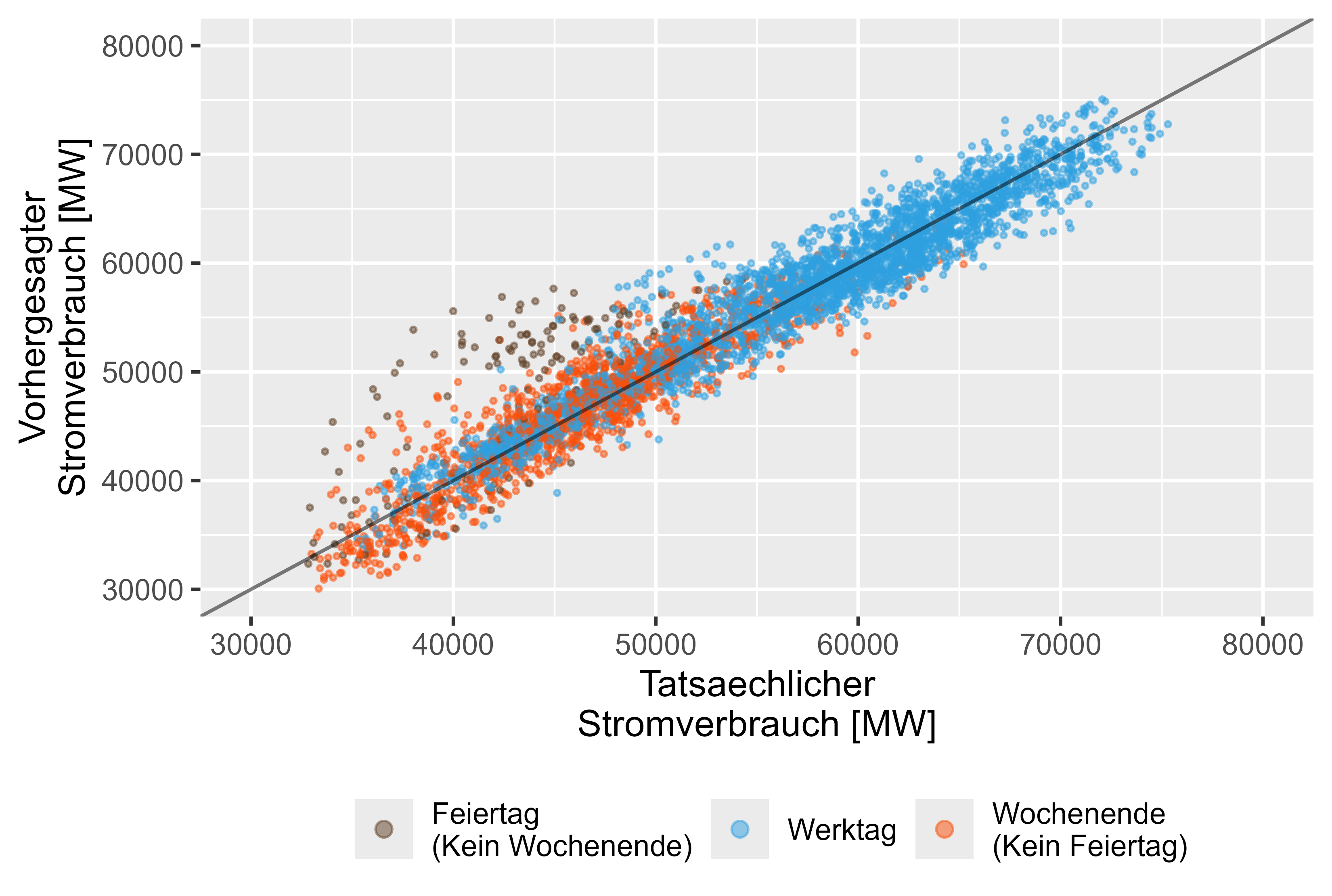Figura 15 Valores previstos frente a valores reales LHM + DHR, modelo conjunto
La figura 16 muestra el pronóstico para enero de 2024. Parece razonable.
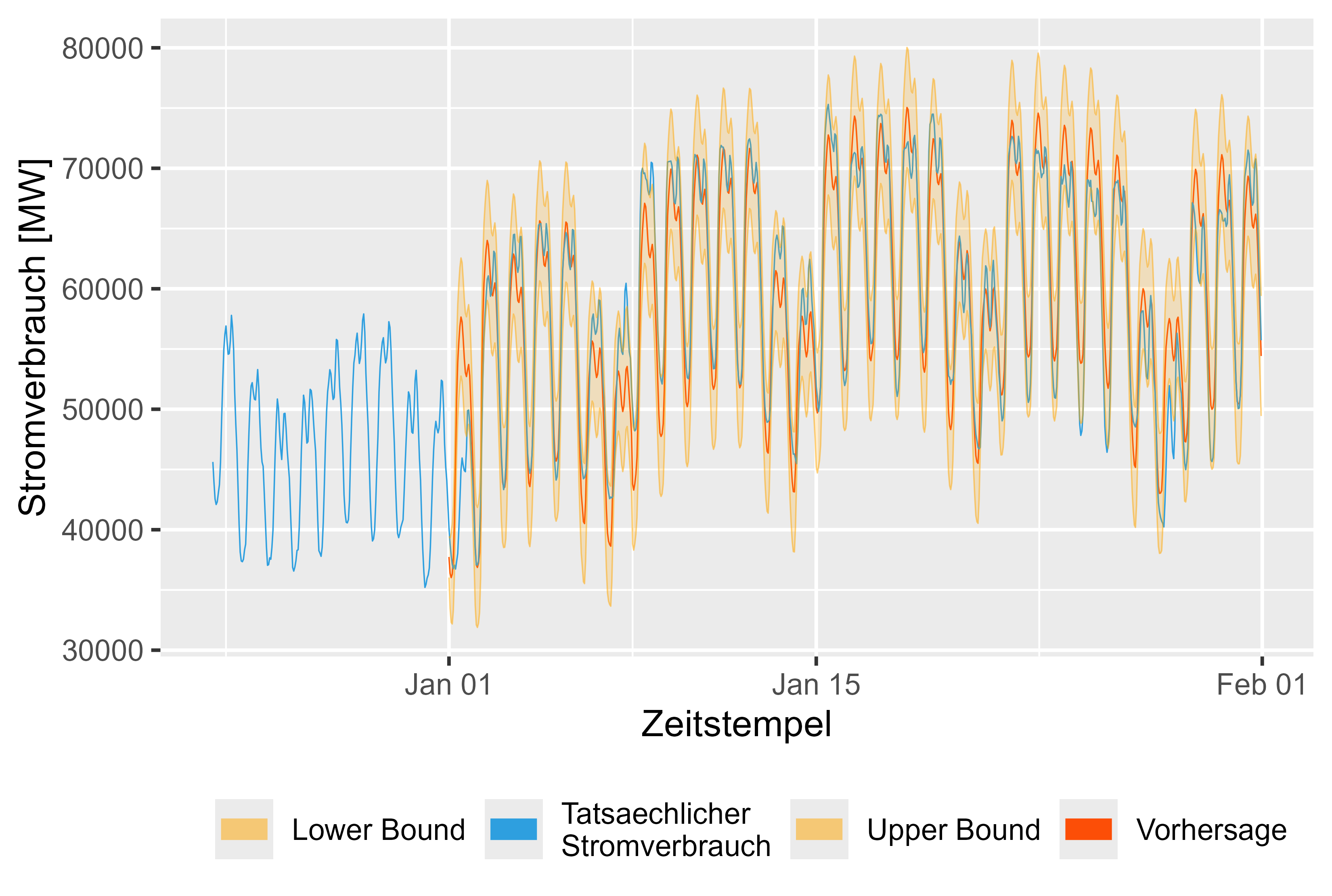Figura 16 Pronóstico versus valores reales LHM + DHR para enero de 2024
Además, los residuos del modelo en comparación con el modelo SMARD parecen buenos. Hay pocos picos que podrían ser significativos y pueden prepararse mejor mediante modelos. Pero en general un resultado sólido.
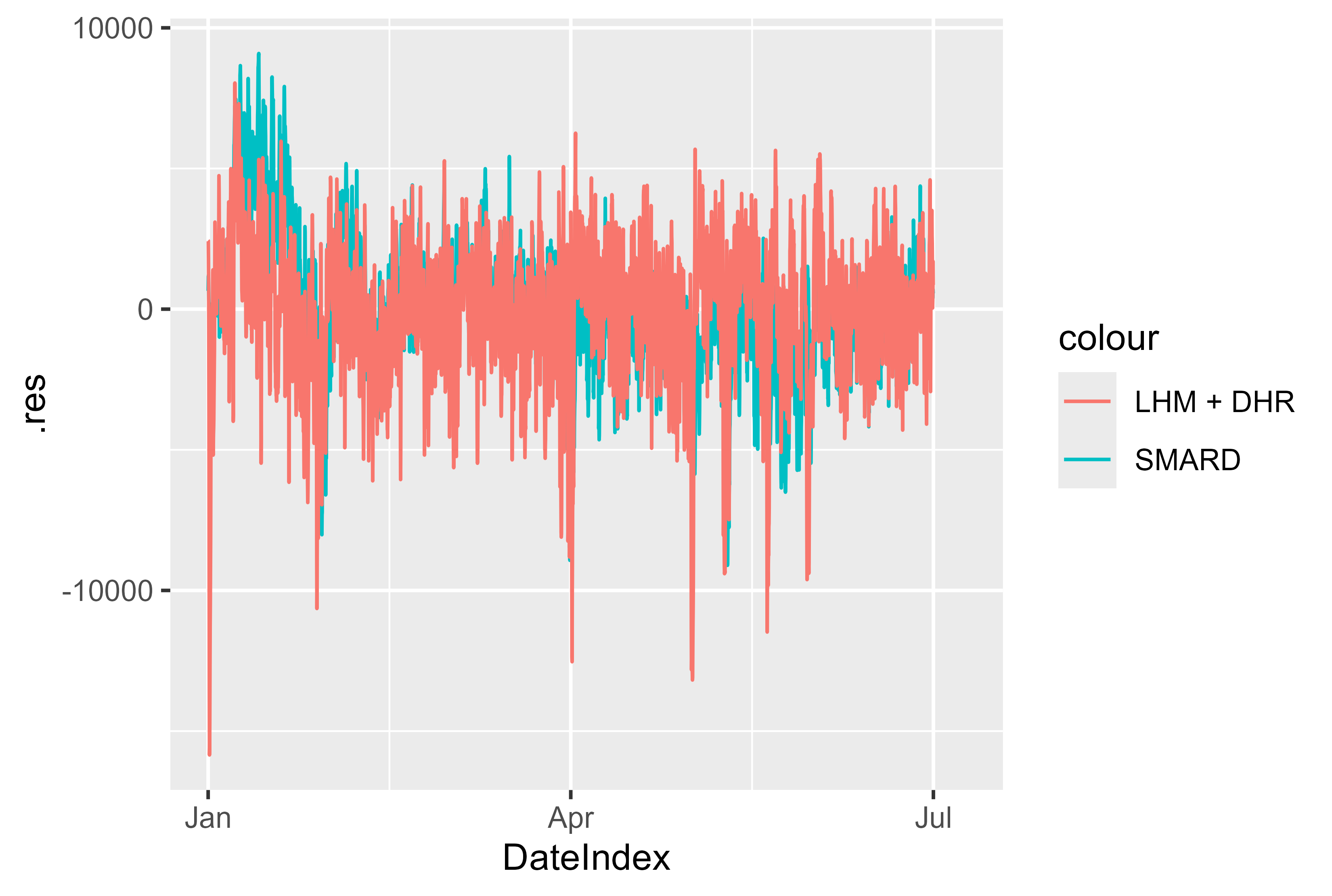Figura 17 Residuos LHM + DHR de enero - julio de 2024
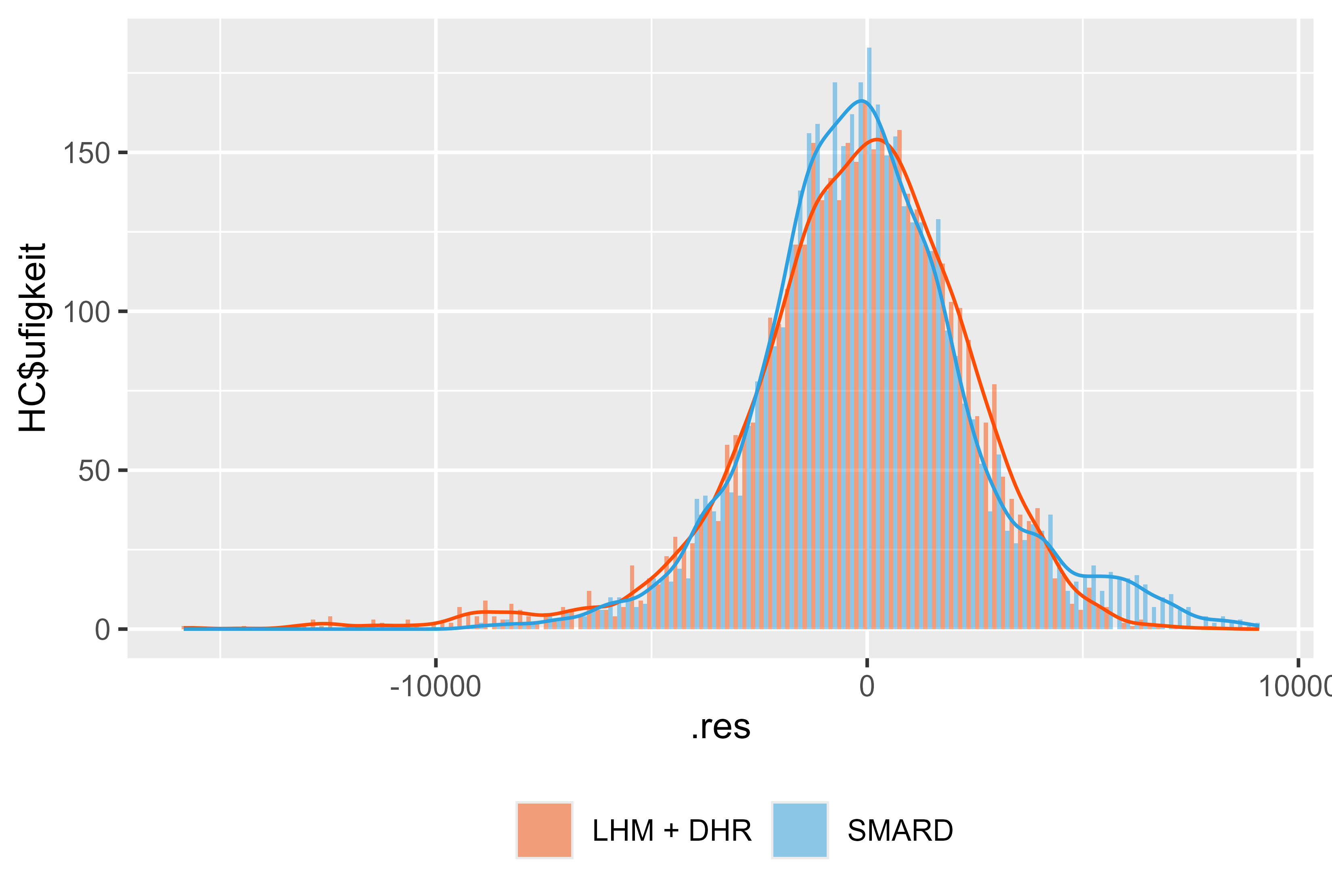Figura 18 Residuos LHM + DHR de enero - julio de 2024
| Índice | Nombre del modelo | RMSE | MAPA | MAE | Ensamblado |
|---|---|---|---|---|---|
| 2 | Observaciones reales | 0.000 | 0.000000 | 0.000 | VERDADERO |
| 3 | inteligente | 2480.693 | 3.602140 | 1869.466 | FALSO |
| 4 | inteligente | 2480.693 | 3.602140 | 1869.466 | VERDADERO |
| 5 | versión_5 | 2626.807 | 3.816012 | 1937.670 | VERDADERO |
| 6 | versión_0 | 2613.258 | 3.846888 | 1946.314 | VERDADERO |
| 7 | versión_7 | 2770.359 | 4.107272 | 2076.045 | VERDADERO |
| 8 | versión_8 | 2775.441 | 4.146788 | 2091.153 | VERDADERO |
| 9 | versión_9 | 2887.179 | 4.177841 | 2100.381 | VERDADERO |
| 10 | versión_6 | 2906.242 | 4.216517 | 2142.092 | VERDADERO |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSO |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSO |
| 13 | versión_4 | 2875.929 | 4.535388 | 2255.645 | VERDADERO |
| 14 | versión_2 | 2905.990 | 4.580770 | 2279.624 | VERDADERO |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | FALSO |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | FALSO |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | FALSO |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSO |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSO |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | FALSO |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | FALSO |
| 24 | profeta_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | FALSO |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | FALSO |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | FALSO |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | FALSO |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | FALSO |
| 29 | versión_3 | 3546.729 | 5.064654 | 2570.530 | VERDADERO |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | FALSO |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | FALSO |
| 32 | versión_1 | 4495.568 | 6.483477 | 3229.647 | VERDADERO |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | FALSO |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | FALSO |
| 35 | media_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | FALSO |
| 36 | ingenuo_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | FALSO |
| 37 | deriva_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | FALSO |
NOTA:
Consulte ejemplo/ensemble_model_2022_forecast o ejemplo/ensemble_model_2023_forecast
Podríamos incluir más factores como:
