Dropout NeuralNetworks
1.0.0
En este proyecto de investigación, me centraré en los efectos de cambiar las tasas de deserción escolar en el conjunto de datos MNIST. Mi objetivo es reproducir la siguiente figura con los datos utilizados en el trabajo de investigación. El propósito de este proyecto es aprender cómo se produjo la figura del aprendizaje automático. Específicamente, conocer los efectos en el error de clasificación al cambiar/no cambiar la probabilidad de abandono.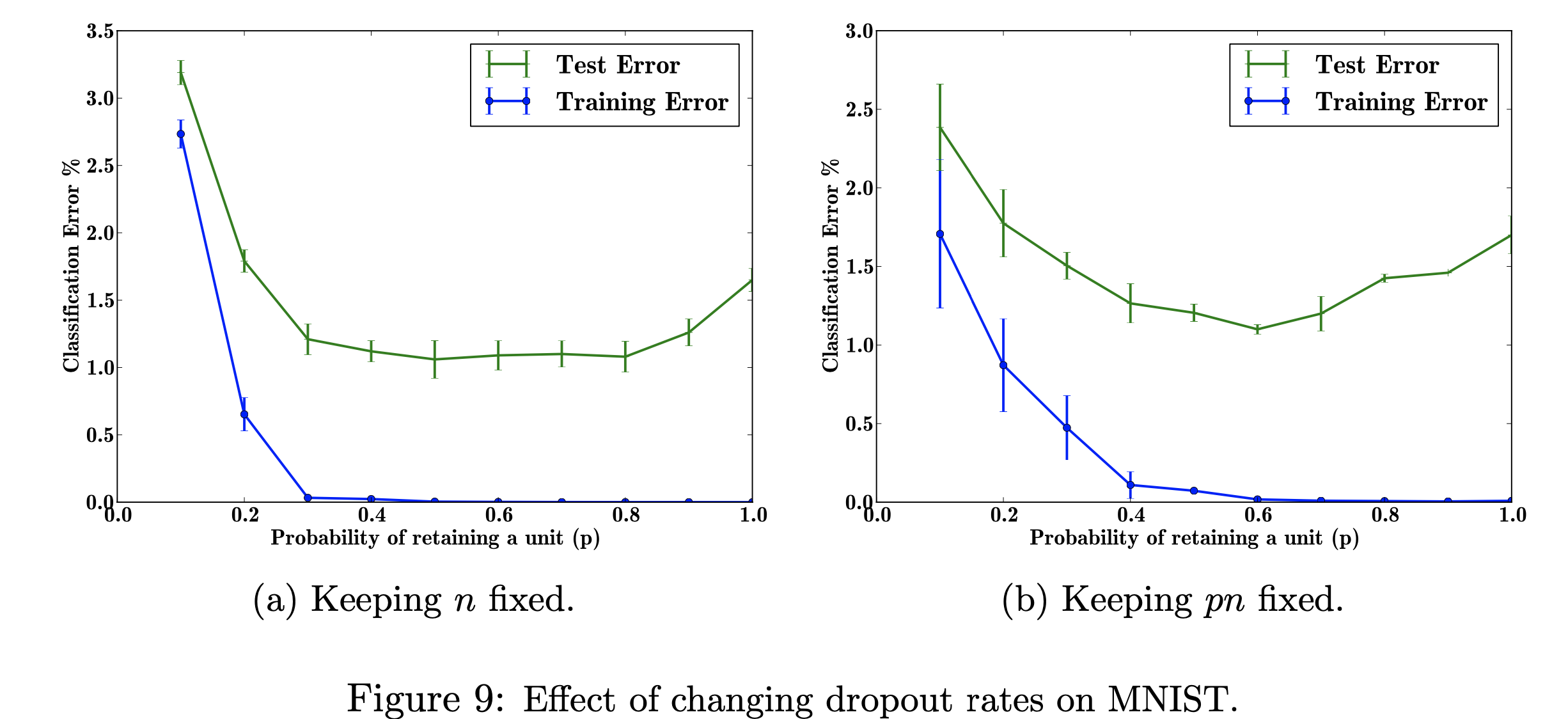
Figura referenciada de: Srivastava, N., Hinton, G., Krizhevsky, A., Krizhevsky, I., Salakhutdinov, R., Abandono: una forma sencilla de evitar el sobreajuste de las redes neuronales, Figura 9
Utilicé TensorFlow para ejecutar el abandono en el conjunto de datos MNIST y Matplotlib para ayudar a recrear la figura en el artículo. También utilicé una biblioteca decimal integrada para calcular los diferentes valores de p, de 0,0 a 1,0. La biblioteca "csv" se importó para agregar datos ejecutados previamente en un archivo CSV, para ahorrar tiempo en el cálculo de los valores de p ya calculados. Se importó Numpy para que el trazado tuviera el mismo tamaño de paso en los ejes x e y. Por último, importé "os" para poder deshacerme de un error debido al uso de una CPU en lugar de una GPU.
Explorar los efectos de los valores variables del hiperparámetro ajustable 'p' (la probabilidad de retener una unidad en la red) y el número de capas ocultas, 'n', que afectan las tasas de error. Cuando el producto de p y n es fijo, podemos ver que la magnitud del error para valores pequeños de p se ha reducido (fig. 9a) en comparación con mantener constante el número de capas ocultas (fig. 9b).
Con datos de entrenamiento limitados, muchas relaciones complicadas entre entradas/salidas serán el resultado del ruido de muestreo. Existirán en el conjunto de entrenamiento, pero no en los datos de prueba reales, incluso si se extraen de la misma distribución. Esta complicación lleva al sobreajuste, este es uno de los algoritmos que ayudan a evitar que esto ocurra. La entrada para esta figura es un conjunto de datos de dígitos escritos a mano, y la salida después de agregar el abandono son valores diferentes que describen el resultado de aplicar el método de abandono. Con todo, se produce menos error después de agregar el abandono.
Un problema del mundo real al que esto se puede aplicar es la búsqueda en Google: alguien puede estar buscando el título de una película pero es posible que solo esté buscando imágenes porque aprende más visualmente. Por lo tanto, eliminar las partes textuales o las explicaciones breves le ayudará a centrarse en las características de la imagen. El artículo indica de dónde recuperan los datos (http://yann.lecun.com/exdb/mnist/). Cada imagen es una representación de 28x28 dígitos. Las etiquetas y parecen ser las columnas de datos de la imagen.
Mi objetivo al reproducir esta figura es probar/entrenar los datos y calcular el error de clasificación para cada probabilidad de p (probabilidad de retener una unidad en la red). Mi objetivo es hacer que p aumente a medida que el error disminuye para mostrar que mi implementación es válida, y ajustaré este hiperparámetro para obtener el mismo resultado. Haré esto recorriendo todos los datos de entrenamiento y prueba usando una arquitectura 784-2048-2048-2048-10 y mantendré el n fijo y luego cambiaré el pn para que se arregle. Luego recopilaré/escribiré los datos en un archivo csv. Este archivo csv contendrá todos los datos necesarios para generar las cifras. En este proyecto, aprenderé cómo la tasa de abandono puede beneficiar el error general en una red neuronal.
Haga clic para ver
