Resuelve el rompecabezas de la Torre de Hanoi mediante aprendizaje por refuerzo.
En un entorno Python con Numpy y Pandas instalados, ejecute el script hanoi.py para producir los tres gráficos que se muestran en la sección Resultados. El script se puede adaptar fácilmente para jugar con un número diferente de discos N , por ejemplo.
El aprendizaje por refuerzo ha recibido recientemente un renovado interés con la paliza de un jugador humano profesional de Go por parte del AlphaGo de Google Deepmind. Aquí se resuelve un rompecabezas más sencillo: el juego de la Torre de Hanoi. La implementación sigue el algoritmo Q-learning propuesto originalmente por Watkins & Dayan [1].
El juego Torre de Hanoi consta de tres clavijas y varios discos de diferentes tamaños que pueden deslizarse sobre las clavijas. El rompecabezas comienza con todos los discos apilados en la primera clavija en orden ascendente, con el más grande abajo y el más pequeño arriba. El objetivo del juego es mover todos los discos a la tercera clavija. Los únicos movimientos legales son aquellos que llevan el disco superior de una clavija a otra, con la restricción de que un disco nunca puede colocarse sobre un disco más pequeño. La Figura 1 muestra la solución óptima para 4 discos.

Figura 1. Solución animada del rompecabezas de la Torre de Hanoi para 4 discos. (Fuente: Wikipedia).
Siguiendo a Anderson [2], representamos el estado del juego mediante tuplas, donde el i- ésimo elemento denota en qué clavija está el i- ésimo disco. Los discos están etiquetados en orden creciente de tamaño. Así, el estado inicial es (111) y el estado final deseado es (333) (Figura 2).
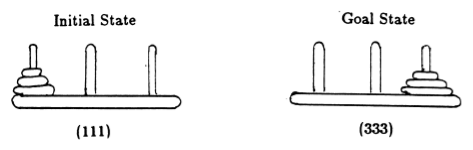
Figura 2. Estados inicial y objetivo del rompecabezas de la Torre de Hanoi con 3 discos. (De [2]).
Los estados del rompecabezas y las transiciones entre ellos correspondientes a movimientos legales forman el gráfico de transición de estados del rompecabezas, que se muestra en la Figura 3.
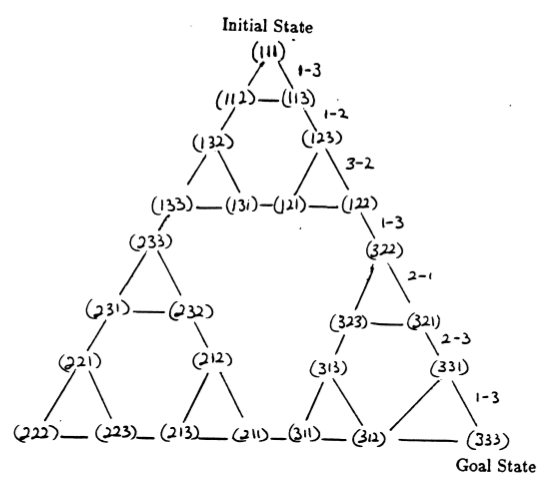
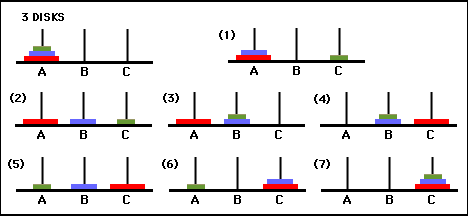
Figura 3. Gráfico de transición de estado para el rompecabezas de tres discos de la Torre de Hanoi (arriba) y la correspondiente solución óptima de 7 movimientos (abajo), que sigue la ruta del lado derecho del gráfico. (De [2] y Mathforum.org).
El número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanoi es 2 N - 1, donde N es el número de discos. Por lo tanto, para N = 3, el rompecabezas se puede resolver en 7 movimientos, como se muestra en la Figura 3. En la siguiente sección, describimos cómo se logra esto mediante Q-learning.
R y la matriz Q de 'valor de acción' para 2 discos El primer paso del programa es generar una matriz de recompensa R que capture las reglas del juego y otorgue una recompensa por ganarlo. Para simplificar, la matriz de recompensas se muestra para N = 2 discos en la Figura 4.
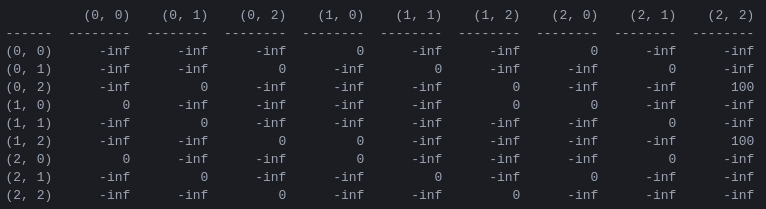
Figura 4. Matriz de recompensas R para un rompecabezas de la Torre de Hanoi con N = 2 discos. El elemento ( i , j ) representa la recompensa por pasar del estado i al j . Los estados están etiquetados por tuplas como en las Figuras 2 y 3, con la diferencia de que las clavijas están indexadas 'pitónicamente' de 0 a 2 en lugar de 1 a 3. A los movimientos que conducen al estado objetivo (2,2) se les asigna una recompensa. de 100, movimientos ilegales de y todos los demás movimientos de 0.
La matriz de recompensa R describe solo recompensas inmediatas : una recompensa de 100 solo se puede lograr desde los penúltimos estados (0,2) y (1,2). En los demás estados, cada uno de los 2 o 3 movimientos posibles tiene una recompensa igual de 0, y no hay ninguna razón aparente para elegir uno sobre el otro.
En última instancia, buscamos asignar un "valor" a cada movimiento posible en cada estado, de modo que maximizando estos valores podamos definir una política que conduzca a la solución óptima. La matriz de 'valores' para cada acción en cada estado se llama Q y puede resolverse o 'aprenderse' recursivamente de manera estocástica, como lo describen Watkins y Dayan [1]. El resultado para 2 discos se muestra en la Figura 5.
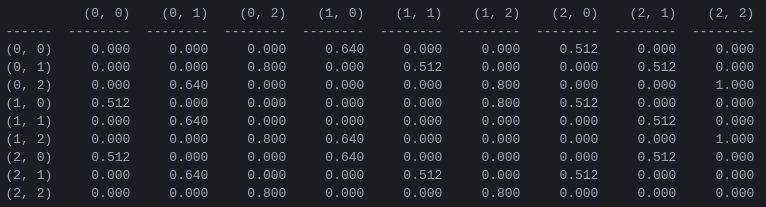
Figura 5. Matriz Q de 'valor de acción' para el juego Torre de Hanoi con 2 discos, aprendido con un factor de descuento de = 0,8, factor de aprendizaje = 1,0 y 1000 episodios de entrenamiento.
Los valores de la matriz Q son esencialmente pesos que se pueden asignar a los vértices del gráfico de transición de estado en la Figura 3, que guían al agente desde el estado inicial al estado objetivo de la manera más corta posible. En este ejemplo, al comenzar en el estado (0,0) y elegir sucesivamente el movimiento con el valor más alto de Q , el lector puede convencerse de que la matriz Q guía al agente a través de la secuencia de estados (0,0) - (1 ,0) - (1,2) - (2,2), que corresponde a la solución óptima de 3 movimientos del juego de la Torre de Hanoi de 2 discos (Figura 6).
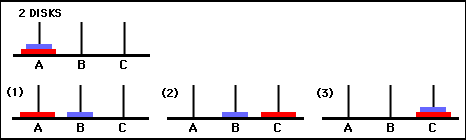
Figura 6. Solución del juego Torre de Hanoi con 2 discos. Los estados consecutivos están representados por (0,0), (1,0), (1,2) y (2,2), respectivamente. (Fuente: mathforum.org).
En este ejemplo, donde la matriz Q ha convergido a su valor óptimo, define una política estacionaria : cada fila contiene una acción con un valor máximo único. Sin embargo, durante el proceso de aprendizaje, diferentes acciones pueden tener el mismo valor de Q (En particular, este es el caso al inicio del entrenamiento cuando Q se inicializa en una matriz de ceros). En las simulaciones presentadas en la siguiente sección, tales situaciones se tratan mediante la siguiente política estocástica : en los casos en que el valor Q máximo se comparte entre varias acciones, se elige una de estas acciones al azar.
El rendimiento del algoritmo Q-learning se puede medir contando el número de movimientos necesarios (en promedio) para resolver el rompecabezas de la Torre de Hanoi. Este número disminuye con el número de episodios de entrenamiento hasta que finalmente alcanza el valor óptimo 2 N - 1, donde N es el número de discos, como se ilustra en la Figura 7 para N = 2, 3 y 4.
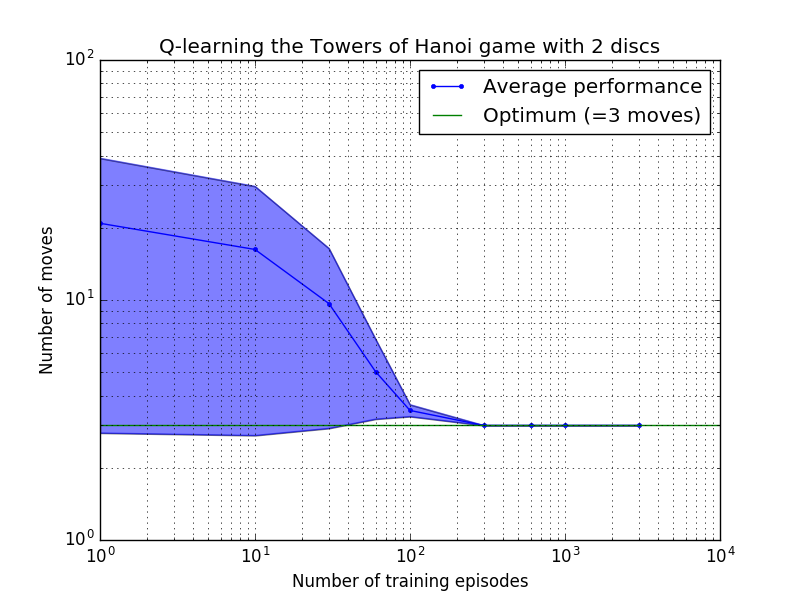
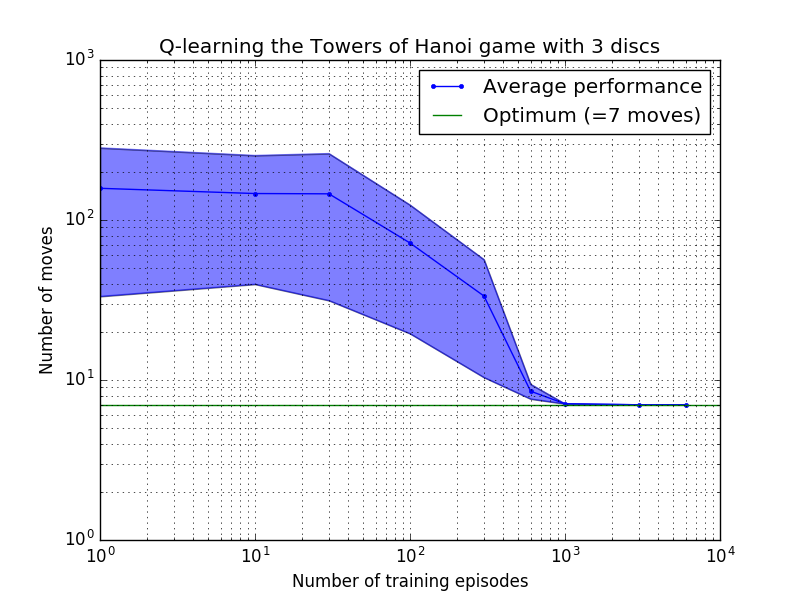
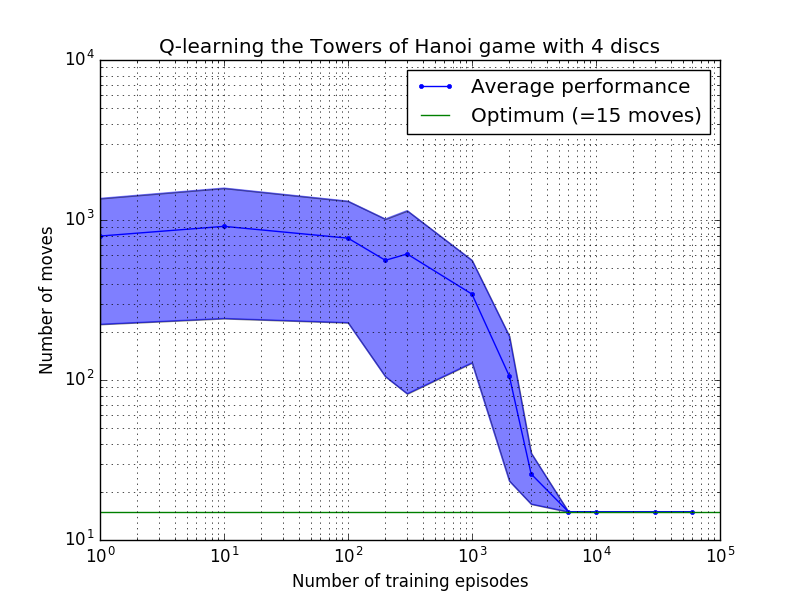
Figura 7. Rendimiento del algoritmo Q-learning para el juego Torre de Hanoi con, de arriba a abajo, 2, 3 y 4 discos. En todos los casos el aprendizaje se realizó con un factor de descuento de = 0,8 y un factor de aprendizaje de = 1,0. La curva azul sólida representa el rendimiento promedio durante 100 épocas de entrenamiento y juego 100 veces para cada política estocástica resultante. Los límites superior e inferior del área sombreada en azul están separados de la media por la desviación estándar estimada. (Para N = 3 y N = 4, el número de episodios de entrenamiento y los tiempos para jugar se redujeron a 10 y 10, respectivamente, debido a limitaciones computacionales).
Una característica interesante de las características de aprendizaje en la Figura 7 es que en todos los casos, el aprendizaje es lento inicialmente y el agente difícilmente lo hace mejor que la política de "entrenamiento cero" de elegir movimientos al azar. En algún momento, el aprendizaje alcanza un "punto de inflexión" y luego converge al número óptimo de movimientos a un ritmo acelerado (aunque esto es algo exagerado por la escala logarítmica).
Un script de Python resuelve con éxito el rompecabezas de la Torre de Hanoi de manera óptima para cualquier número de discos mediante Q-learning. El guión se puede adaptar fácilmente a otros problemas con una matriz de recompensa R diferente.
El número de episodios de entrenamiento necesarios para converger a una solución óptima aumenta enormemente con el número de discos N : para N=2 discos se necesitan ~300 episodios, mientras que para N=4 se necesitan ~6000. Una posible mejora del algoritmo de aprendizaje sería permitirle buscar automáticamente soluciones recursivas, como lo hizo Hengst [3].
[1] Watkins y Dayan, Q-learning , Aprendizaje automático, 8, 279-292 (1992). (PDF).
[2] Anderson, Aprendizaje y resolución de problemas con sistemas conexionistas multicapa , Ph.D. tesis (1986). (PDF).
[3] Hengst, Descubriendo la jerarquía en el aprendizaje por refuerzo con HEXQ , Actas de la Decimonovena Conferencia Internacional sobre Aprendizaje Automático (2002). (PDF).