@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}¿Sabía que neurodiffeq admite paquetes de soluciones y puede usarse para resolver problemas inversos? ¡Mira aquí!
? ¿Ya estás familiarizado con neurodiffeq? ? Vaya a las preguntas frecuentes.
neurodiffeq es un paquete para resolver ecuaciones diferenciales con redes neuronales. Las ecuaciones diferenciales son ecuaciones que relacionan alguna función con sus derivadas. Surgen en diversos dominios científicos y de ingeniería. Tradicionalmente, estos problemas se pueden resolver mediante métodos numéricos (por ejemplo, diferencias finitas, elementos finitos). Si bien estos métodos son eficaces y adecuados, su expresabilidad está limitada por la representación de su función. Sería interesante si pudiéramos calcular soluciones para ecuaciones diferenciales que sean continuas y diferenciables.
Como aproximadores de funciones universales, se ha demostrado que las redes neuronales artificiales tienen el potencial de resolver ecuaciones diferenciales ordinarias (EDO) y ecuaciones diferenciales parciales (EDP) con ciertas condiciones iniciales/de frontera. El objetivo de neurodiffeq es implementar estas técnicas existentes de uso de ANN para resolver ecuaciones diferenciales de una manera que permita que el software sea lo suficientemente flexible para trabajar en una amplia gama de problemas definidos por el usuario.
Como la mayoría de las bibliotecas estándar, neurodiffeq está alojada en PyPI. Para instalar la última versión estable,
pip install -U neurodiffeq # '-U' significa actualizar a la última versión
Alternativamente, puede instalar la biblioteca manualmente para obtener acceso temprano a nuestras nuevas funciones. Esta es la forma recomendada para los desarrolladores que quieran contribuir a la biblioteca.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip install -r requisitos instalación de pipas. # Para realizar cambios en la biblioteca, use `pip install -e .`pytest tests/ # Ejecutar pruebas. Opcional.
Estaremos encantados de ayudarle con cualquier pregunta. Mientras tanto, puedes consultar las preguntas frecuentes.
Para ver tutoriales completos y documentación de neurodiffeq , consulte la documentación oficial.
Además de la documentación, recientemente hemos realizado un vídeo de demostración rápido con diapositivas.
desde neurodiffeq importar diffdesde neurodiffeq.solvers importar Solver1D, Solver2Ddesde neurodiffeq.conditions importar IVP, DirichletBVP2Ddesde neurodiffeq.networks importar FCNN, SinActv
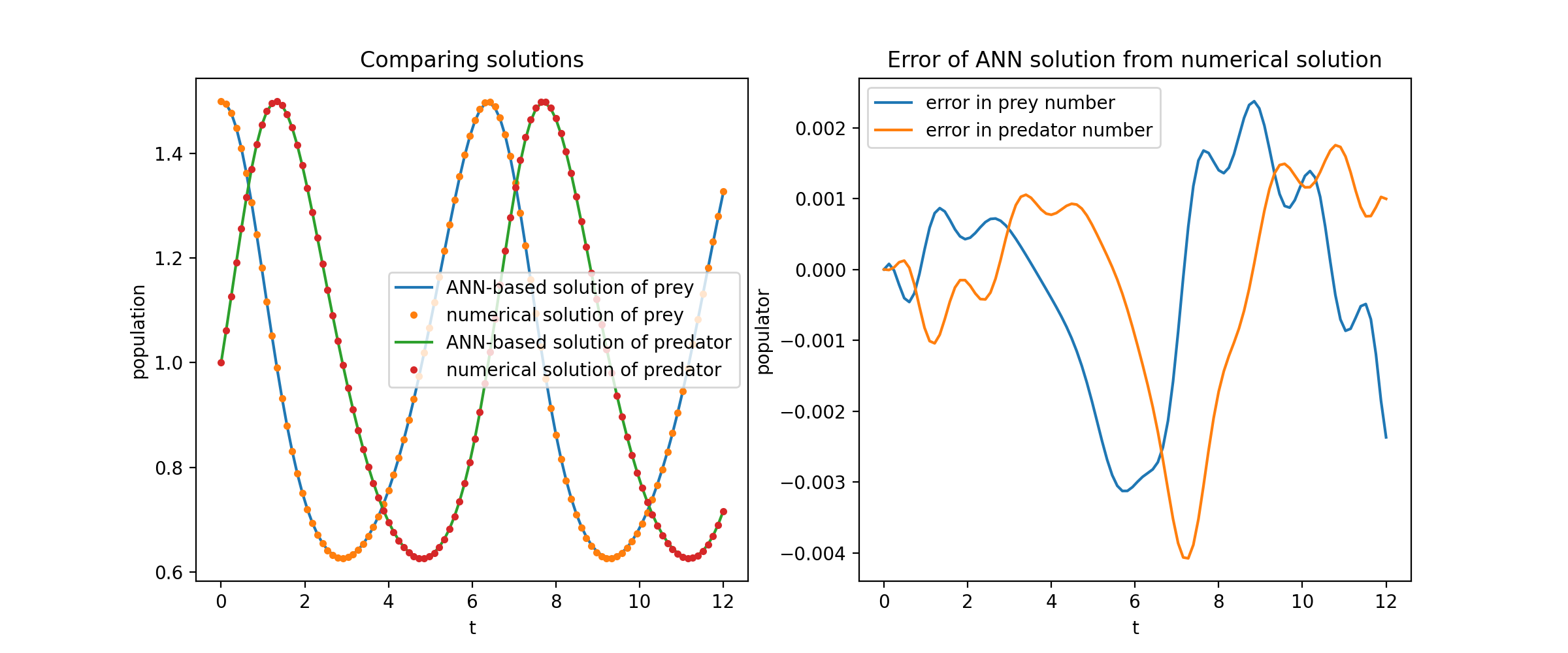
Aquí resolvemos un sistema no lineal de dos EDO, conocido como ecuaciones de Lotka-Volterra. Hay dos funciones desconocidas ( u y v ) y una única variable independiente ( t ).
def ode_system(u, v, t): retorno [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]condiciones = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]redes = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, condiciones, t_min=0.1, t_max=12.0, redes=redes)solver.fit(max_epochs=3000)solución = solver.get_solution()
solution es un objeto invocable, puede pasarle matrices numerosas o tensores de antorcha como
u, v = solución(t, to_numpy=True) # t puede ser np.ndarray o torch.Tensor
Trazar u y v frente a sus soluciones analíticas produce algo como:
Aquí resolvemos una ecuación de Laplace con condiciones de frontera de Dirichlet en un rectángulo. Tenga en cuenta que elegimos la ecuación de Laplace por su simplicidad para calcular la solución analítica. En la práctica, puede intentar cualquier PDE caótica y no lineal , siempre que ajuste el solucionador lo suficientemente bien.
Resolver un sistema PDE 2-D es bastante similar a resolver EDO, excepto que hay dos y x problemas t x problemas de valores límite iniciales, los cuales son compatibles.
def pde_system(u, x, y):return [diff(u, x, orden=2) + diff(u, y, orden=2)]condiciones = [DirichletBVP2D(x_min=0, x_min_val=lambda y: antorcha. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=lambda x: 0, y_max=1, y_max_val=lambda x: 0,
)
]redes = [FCNN(n_input_units=2, n_output_units=1, ocultas_units=(512,))]solver = Solver2D(pde_system, condiciones, xy_min=(0, 0), xy_max=(1, 1), redes=redes) solver.fit(max_epochs=2000)solución = solver.get_solution() La firma de solution para una PDE 2D es ligeramente diferente a la de una ODE. Nuevamente, se necesitan matrices numerosas o tensores de antorcha.
u = solución(x, y, to_numpy=Verdadero)
La evaluación de u en [0,1] × [0,1] produce los siguientes gráficos
| Solución basada en ANN | Residual de PDE |
|---|---|
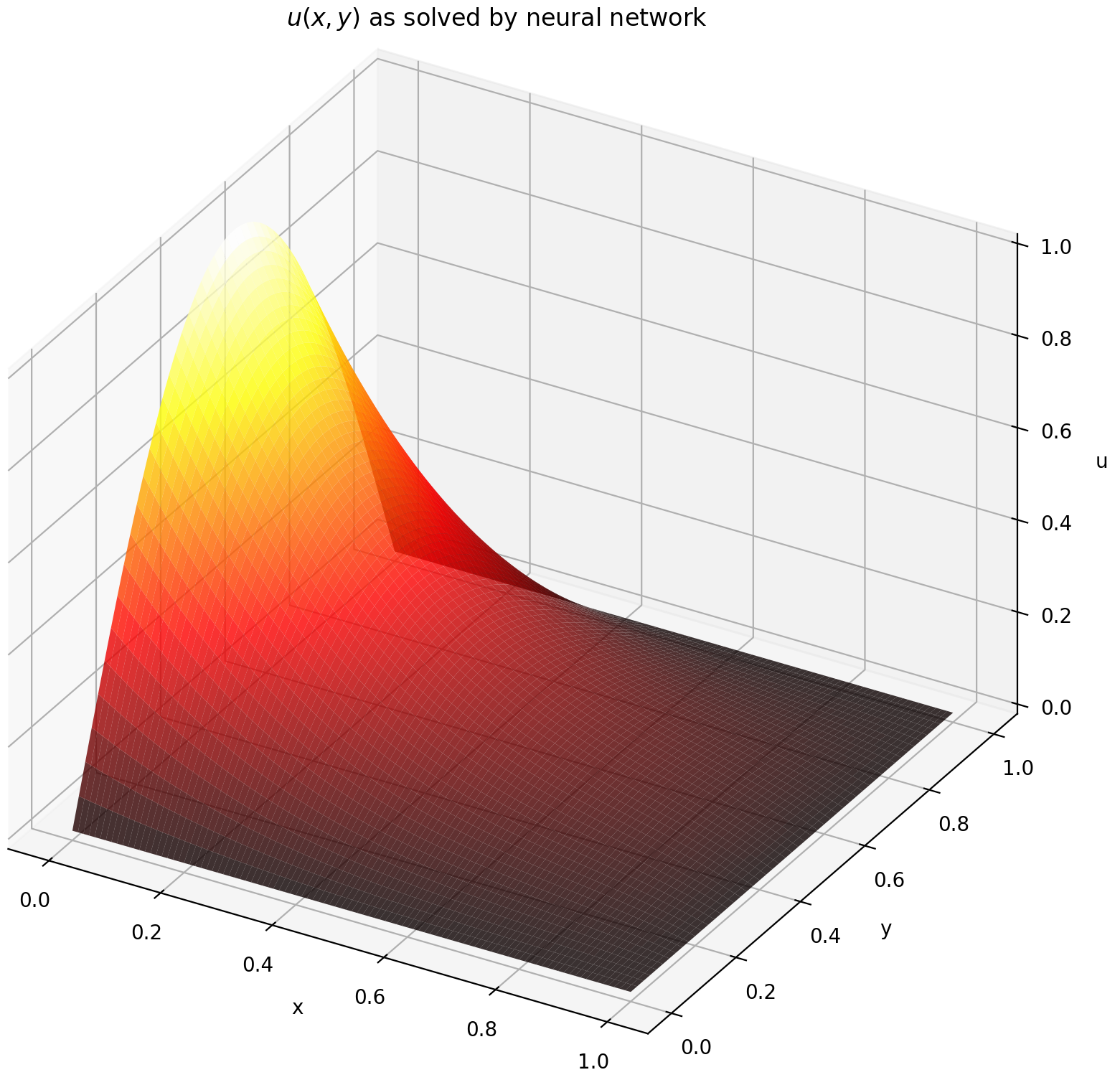 | 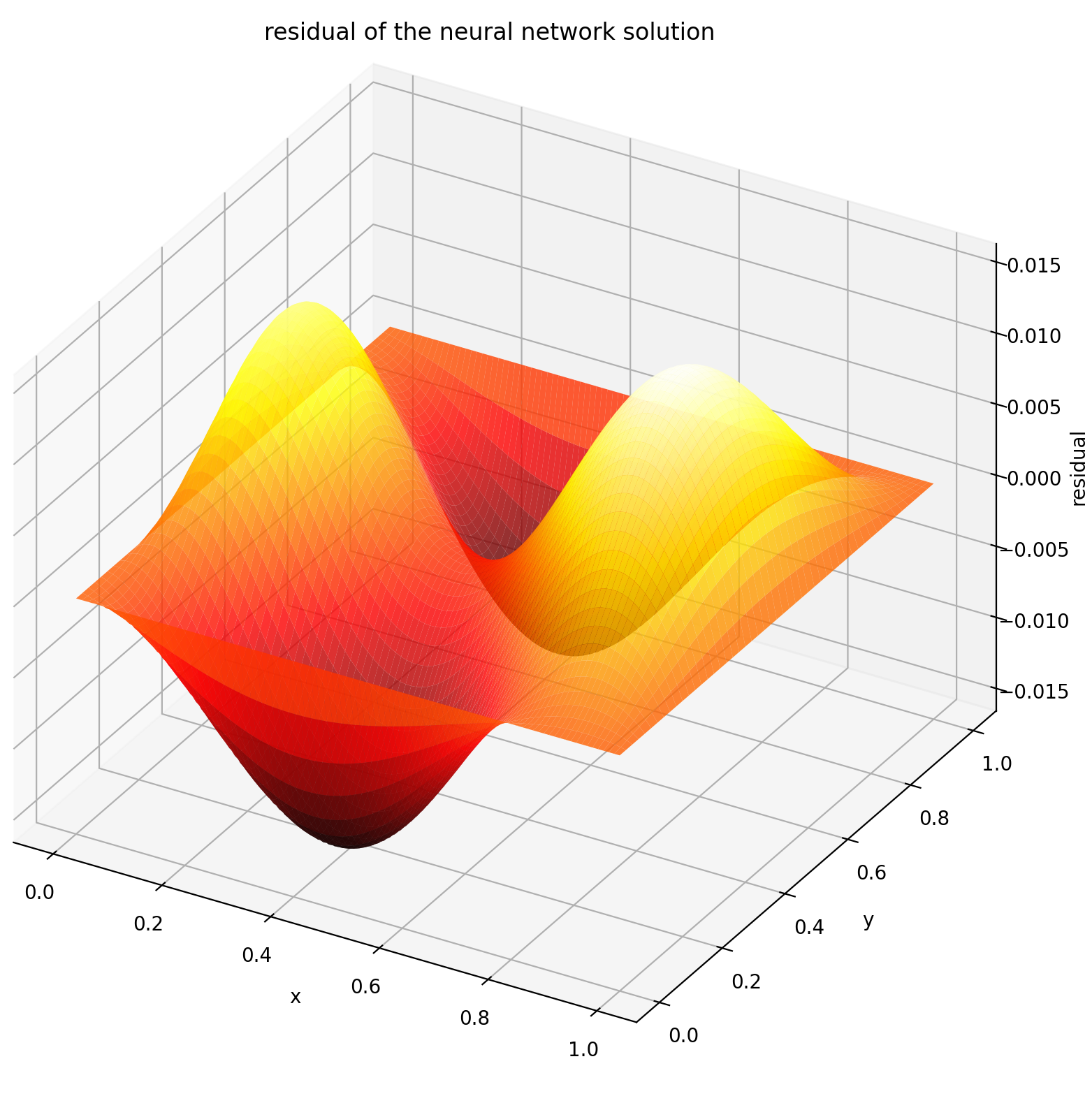 |
Un monitor es una herramienta para visualizar soluciones PDE/ODE, así como el historial de pérdidas y métricas personalizadas durante el entrenamiento. Los usuarios de Jupyter Notebooks deben ejecutar la magia %matplotlib notebook . Para los usuarios de Jupyter Lab, pruebe %matplotlib widget .
de neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
Debería ver los gráficos actualizarse cada 100 épocas , así como en la última época , mostrando dos gráficos: uno para la visualización de la solución en el intervalo [0,12] y el otro para el historial de pérdidas (entrenamiento y validación).
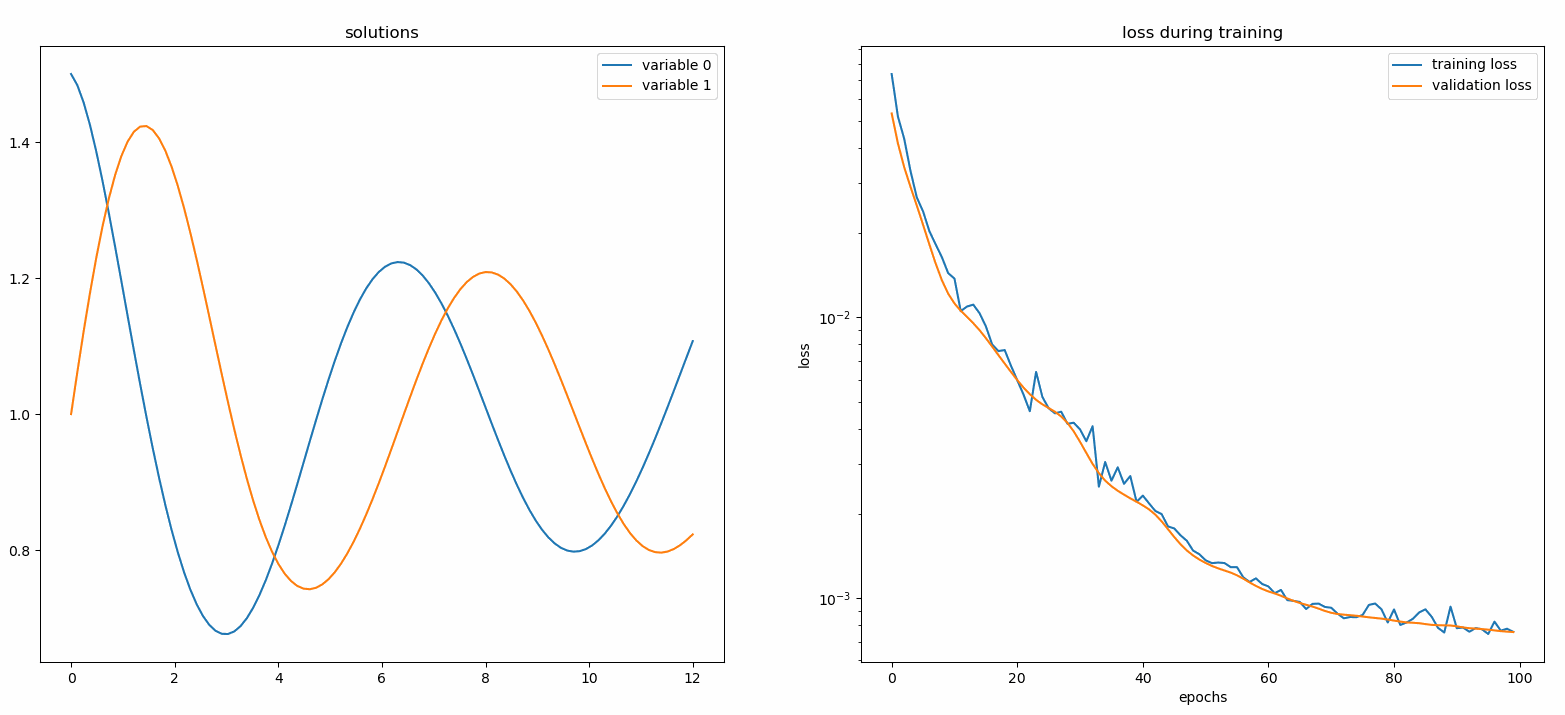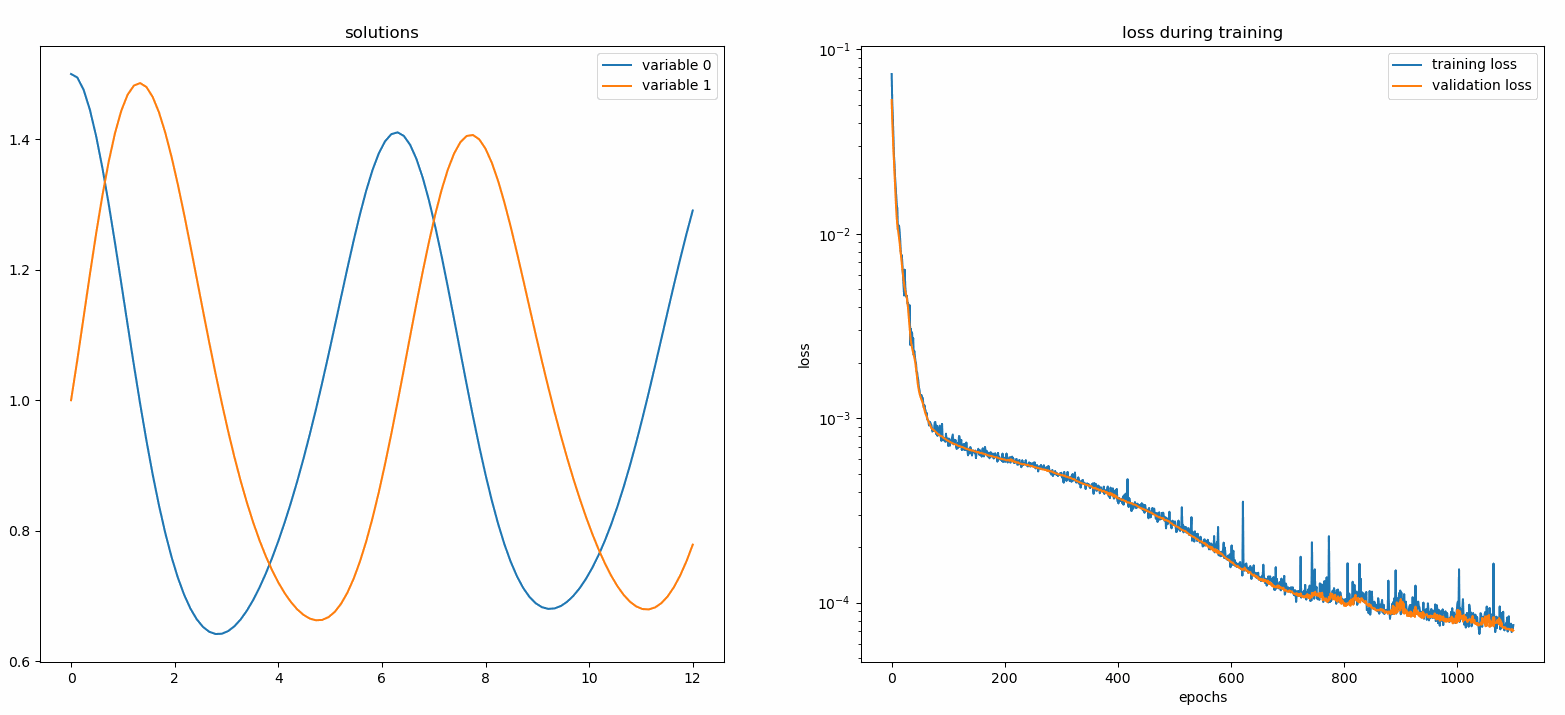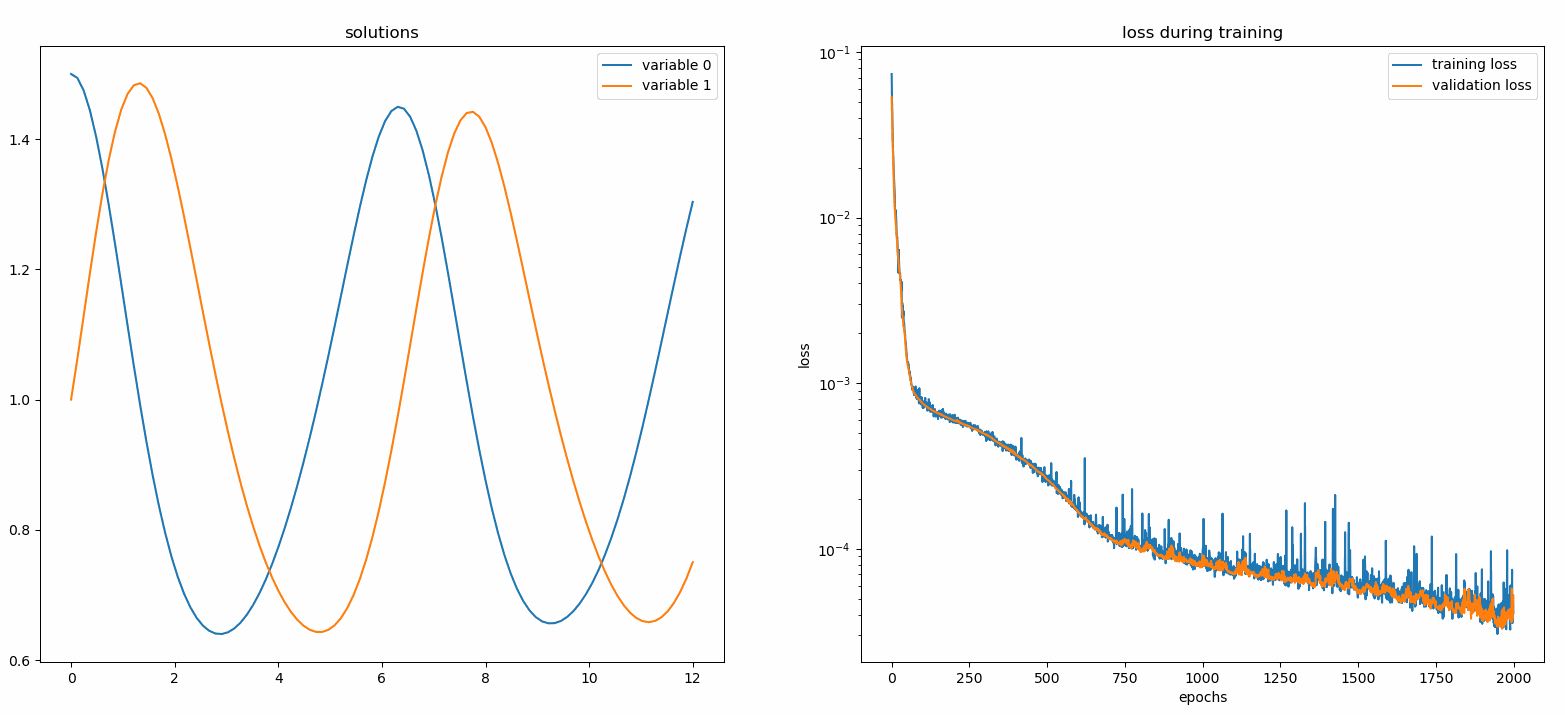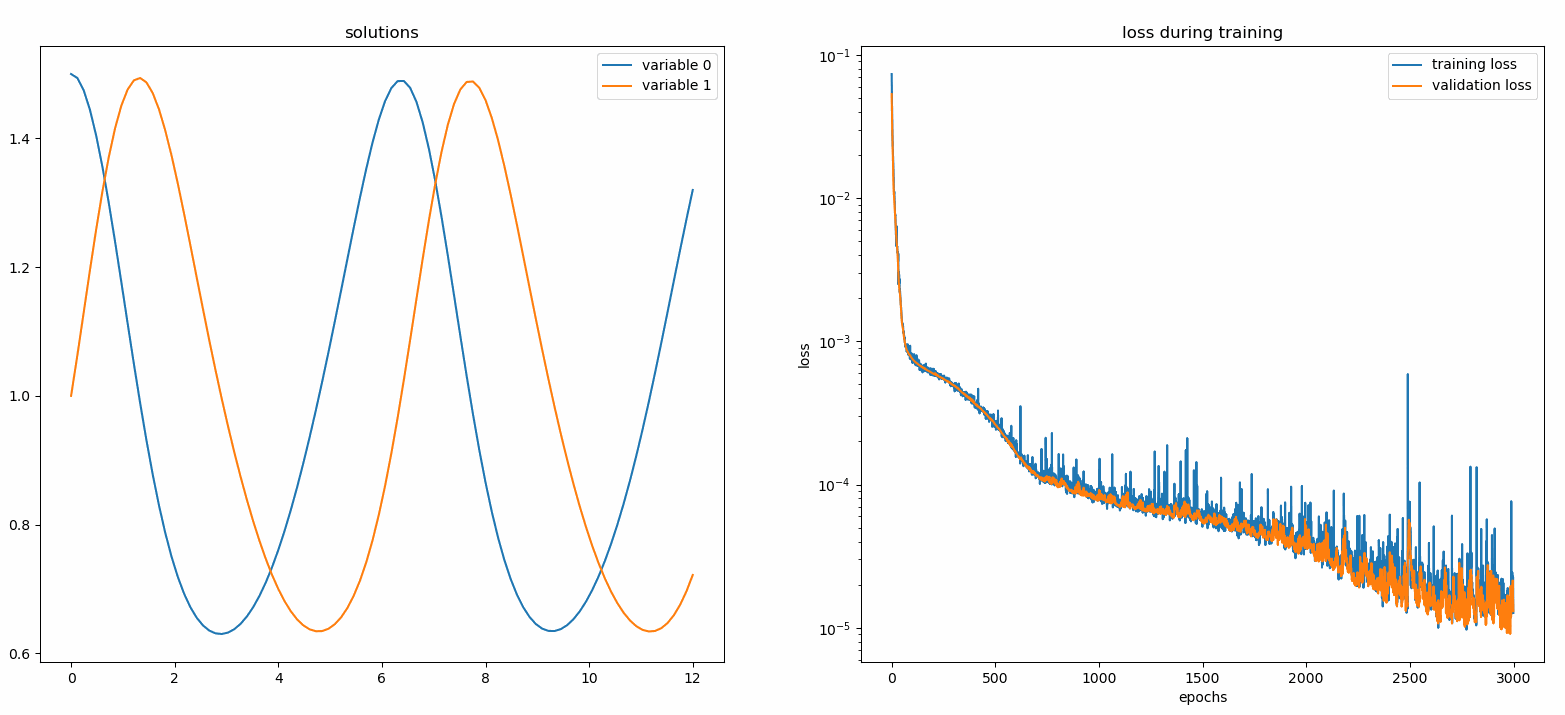
Para mayor comodidad, hemos implementado una FCNN (red neuronal totalmente conectada), cuyas unidades ocultas y funciones de activación se pueden personalizar.
de neurodiffeq.networks importar FCNN# Predeterminado: n_input_units=1, n_output_units=1, hide_units=[32, 32], activación=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., hide_units=[ ..., ..., ...], activación=...) ...redes = [red1, red2, ...]
FCNN suele ser un buen punto de partida. Para usuarios avanzados, los solucionadores son compatibles con cualquier torch.nn.Module personalizado. Las únicas restricciones son:
Los módulos reciben un tensor de forma (None, n_coords) y generan un tensor de forma (None, 1) .
Debe haber un total de módulos n_funcs en nets para pasarlos a solver = Solver(..., nets=nets) .
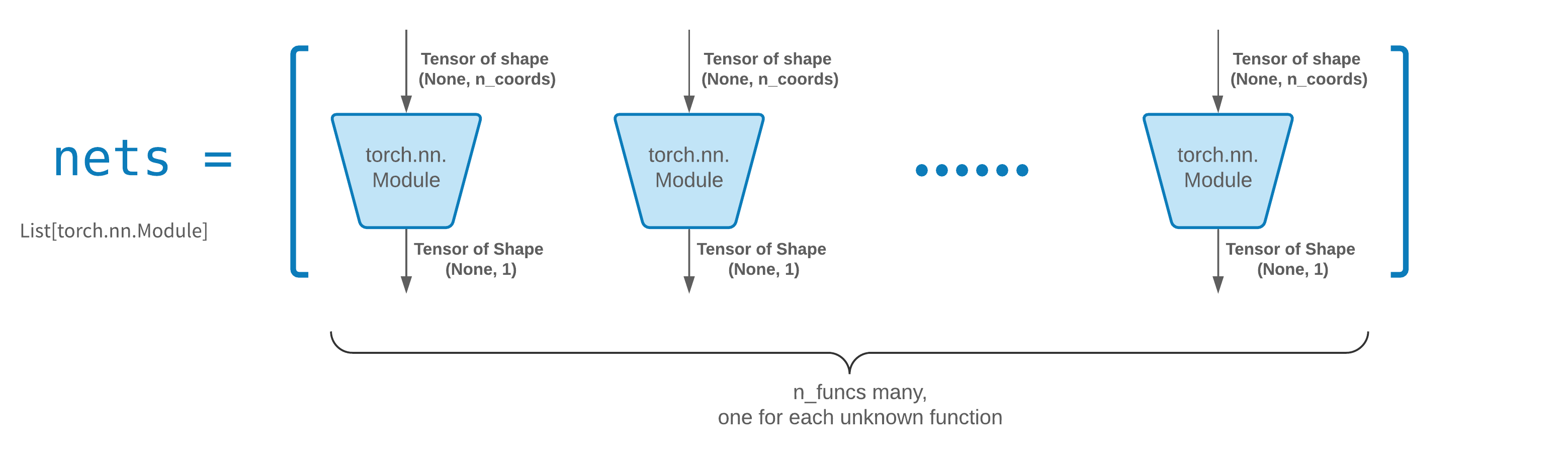
En realidad, neurodiffeq tiene una característica single_net que no obedece las reglas anteriores, que no se tratarán aquí.
Lea el tutorial de PyTorch sobre cómo crear su propia arquitectura de red (también conocida como módulo).
La transferencia de aprendizaje se realiza fácilmente serializando old_solver.nets (una lista de módulos de antorcha) en el disco y luego cargándolos y pasándolos a un nuevo solucionador:
old_solver.fit(max_epochs=...)# ... volcar `old_solver.nets` al disco# ... cargar las redes desde el disco, almacenarlas en alguna variable `loaded_nets`new_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
Actualmente estamos trabajando en funciones contenedoras para guardar/cargar redes y otras variables internas de Solvers. Mientras tanto, puedes leer el tutorial de PyTorch sobre cómo guardar y cargar tus redes.
En neurodiffeq, las redes se entrenan minimizando la pérdida (residuales ODE/PDE) evaluadas en un conjunto de puntos en el dominio. Los puntos se vuelven a muestrear aleatoriamente cada vez. Para controlar el número, la distribución y el dominio delimitador de los puntos muestreados, puede especificar sus propios generator de entrenamiento/validación.
de neurodiffeq.generators importar Generador1D# Predeterminado t_min=0.0, t_max=1.0, método='uniforme', noise_std=Noneg1 = Generador1D(tamaño=..., t_min=..., t_max=..., método=.. ., ruido_std=...)g2 = Generador1D(tamaño=..., t_min=..., t_max=..., método=..., ruido_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
A continuación se muestran algunas distribuciones de muestra de un Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
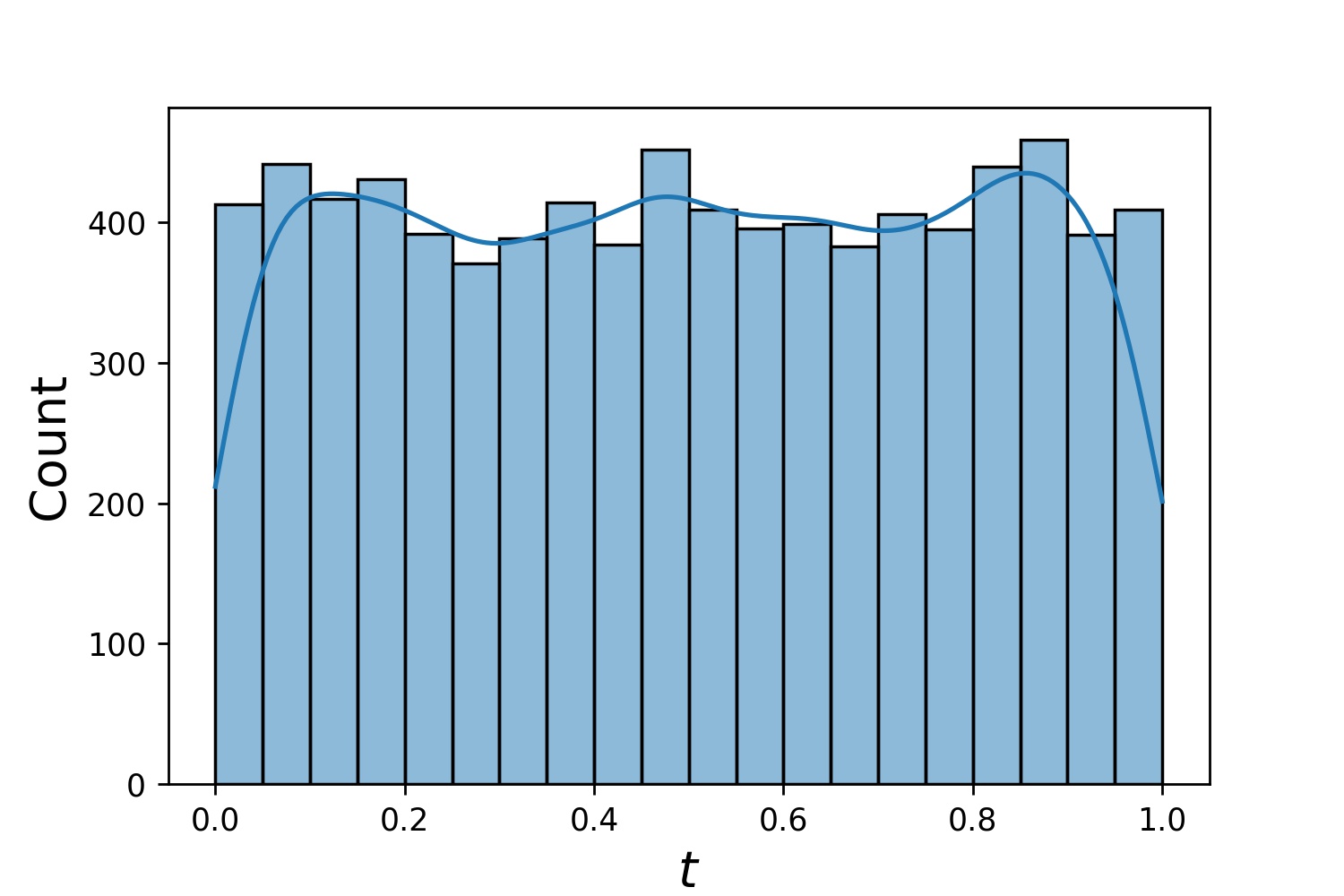 | 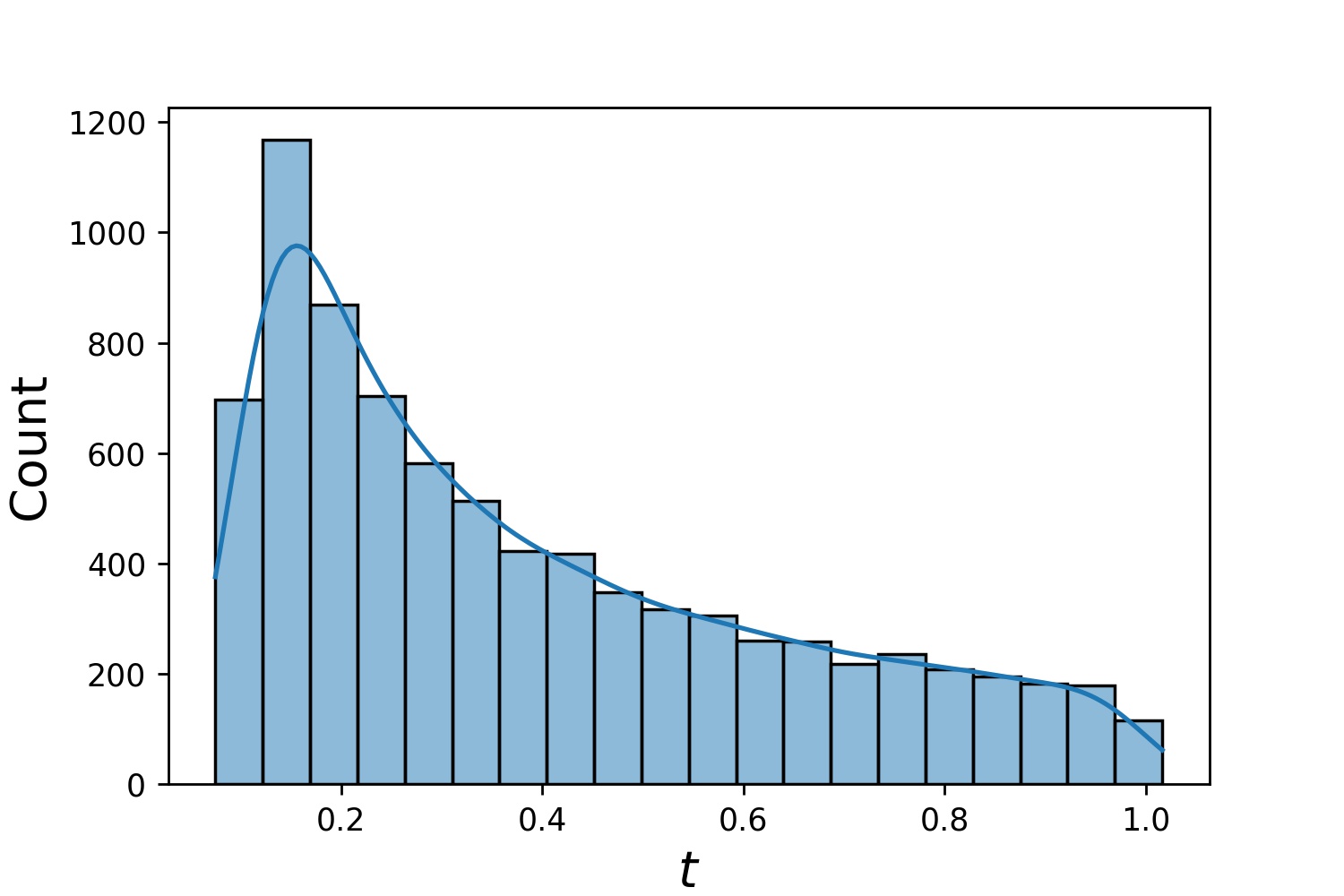 |
Tenga en cuenta que cuando se especifican train_generator y valid_generator , t_min y t_max se pueden omitir en Solver1D(...) . De hecho, incluso si pasa t_min , t_max , train_generator , valid_generator juntos, t_min y t_max seguirán siendo ignorados.
Otra característica interesante de los generadores es que puedes concatenarlos, por ejemplo
g1 = Generador2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generador2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2
Aquí, g será un generador que generará las muestras combinadas de g1 y g2
g1 | g2 | g1 + g2 |
|---|---|---|
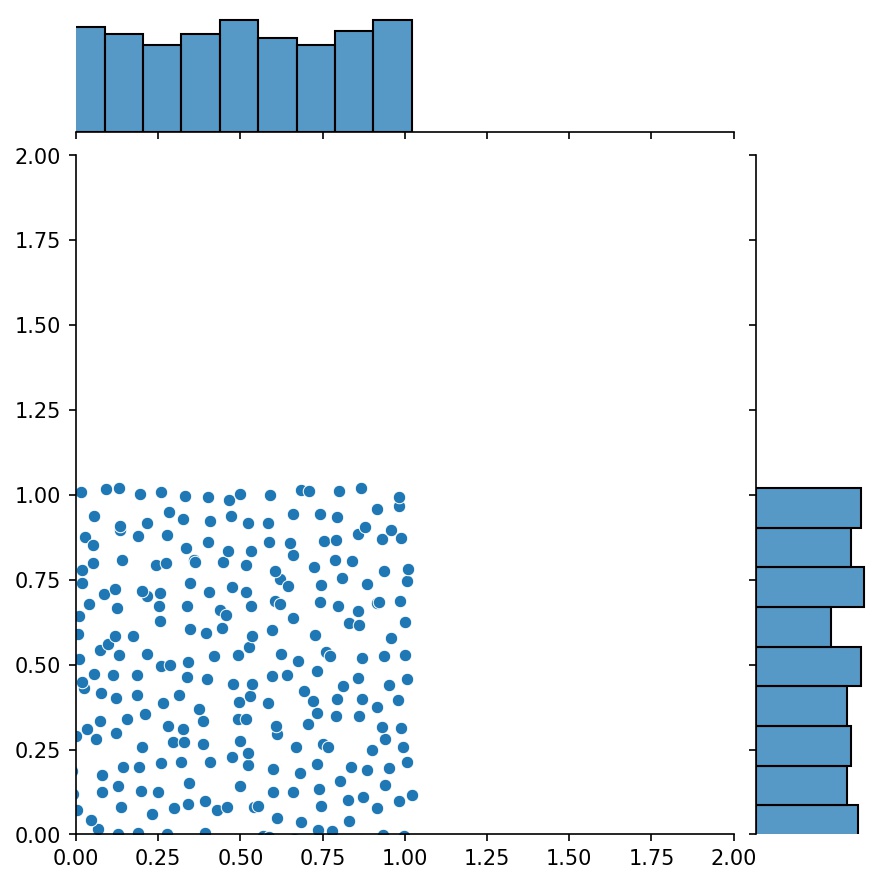 | 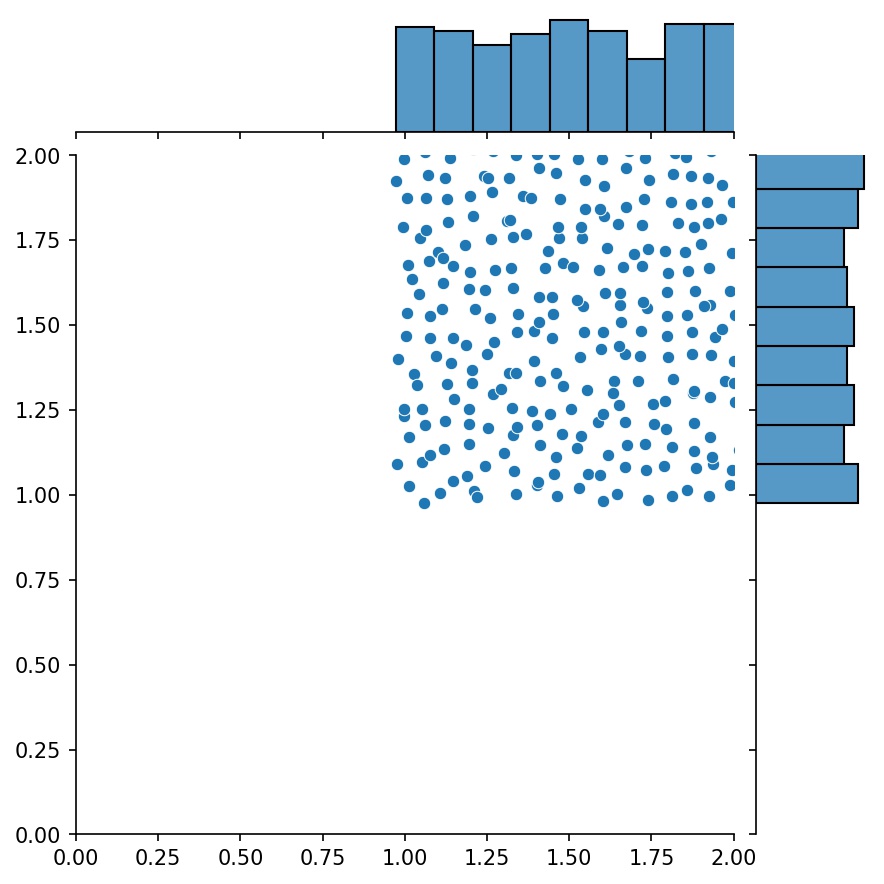 |  |
Puede utilizar Generator2D , Generator3D , etc. para puntos de muestreo en dimensiones superiores. Pero también hay otra manera
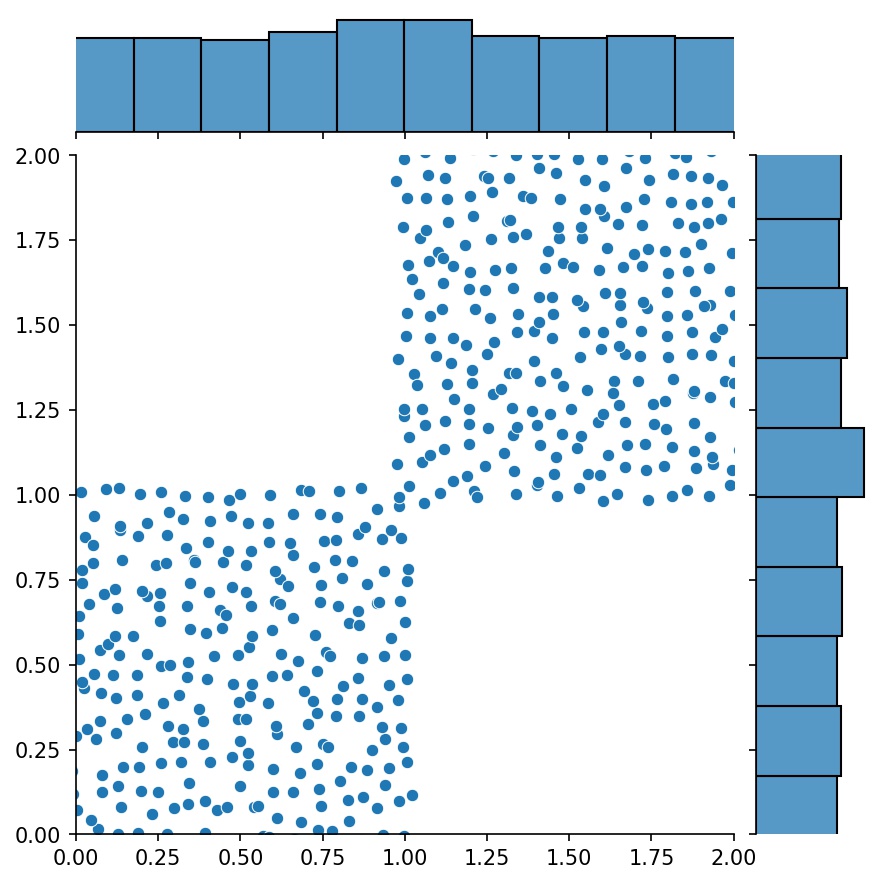
g1 = Generador1D(1024, 2.0, 3.0, método='uniforme')g2 = Generador1D(1024, 0.1, 1.0, método='ruidoso-espaciado logarítmicamente', ruido_std=0.001)g = g1 * g2
Aquí, g será un generador que producirá 1024 puntos en un rectángulo 2D (2,3) × (0.1,1) cada vez. Las coordenadas x de ellos se extraen de (2,3) usando la estrategia uniform y la coordenada y extraída de (0.1,1) usando la estrategia log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
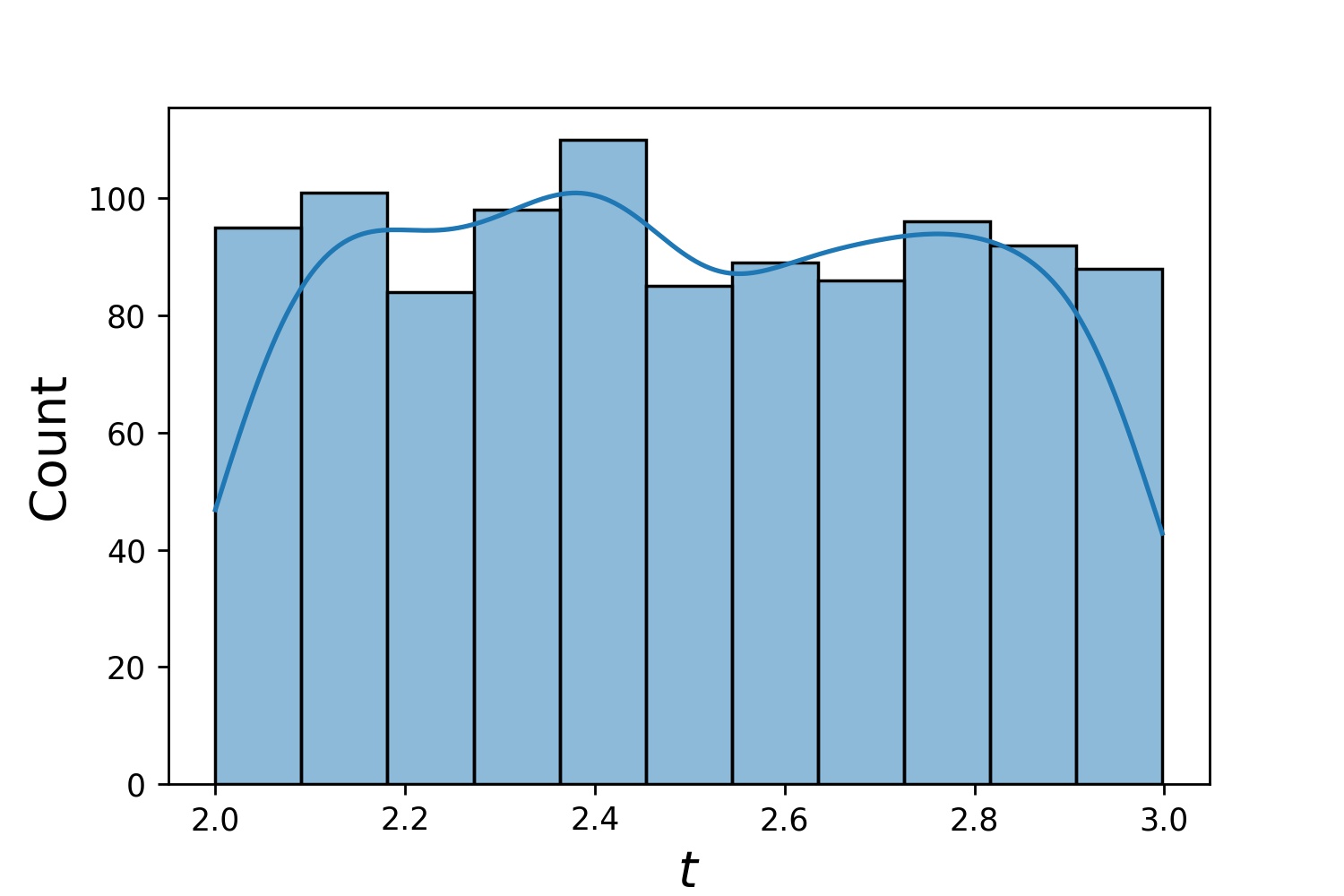 | 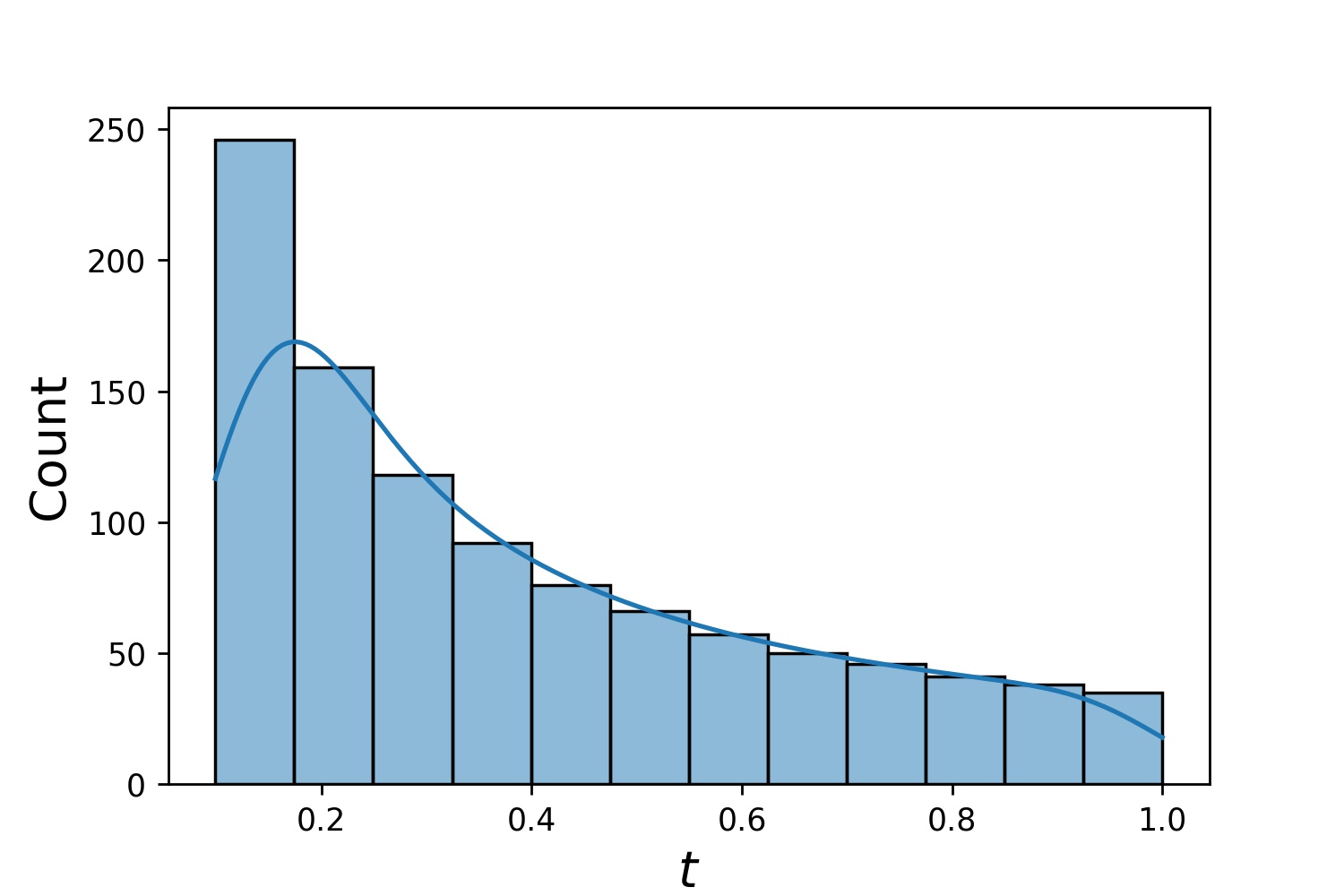 | 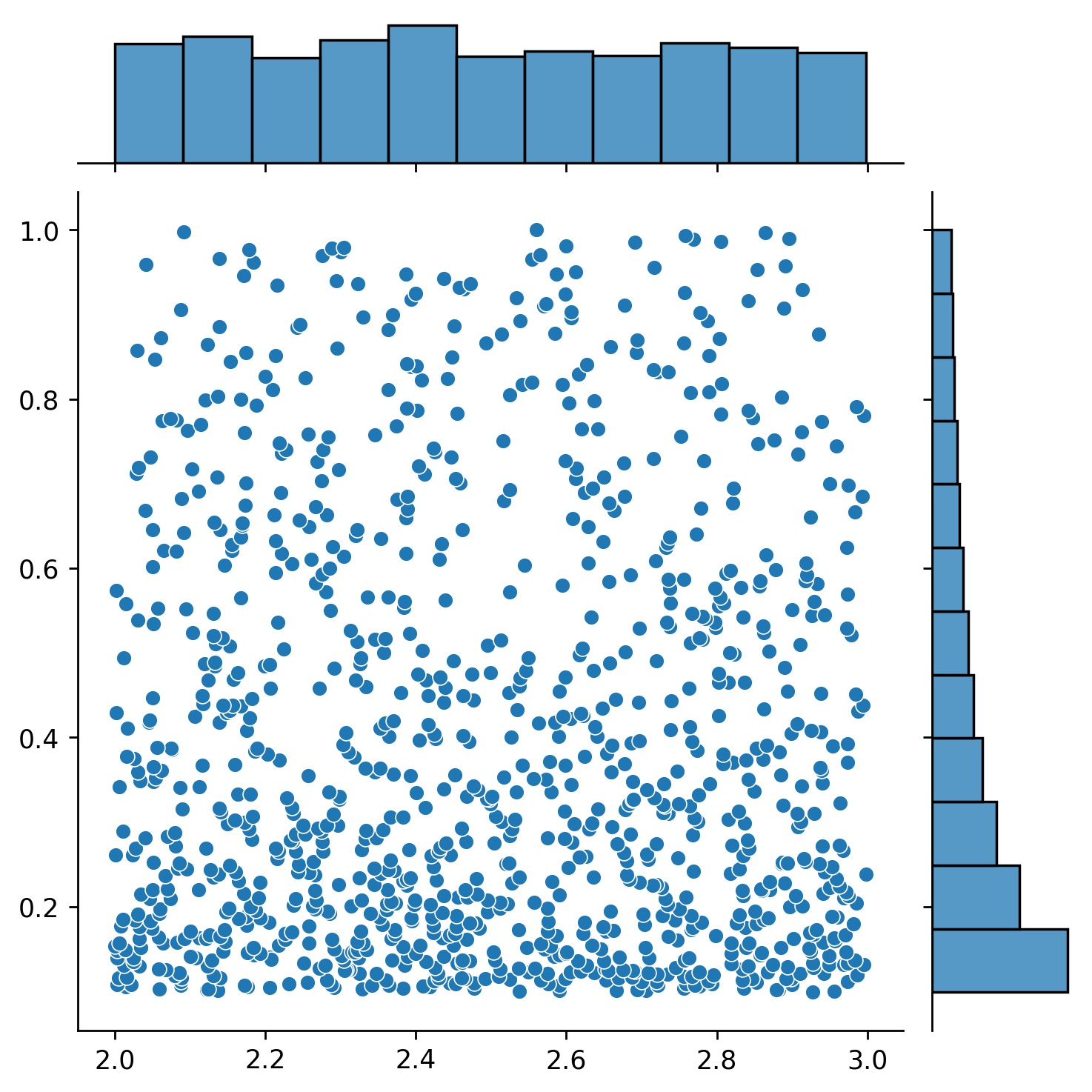 |
A veces resulta interesante resolver un conjunto de ecuaciones a la vez. Por ejemplo, es posible que desees resolver ecuaciones diferenciales de la forma du/dt + λu = 0 bajo la condición inicial u(0) = U0 . Es posible que desees resolver esto para todos λ y U0 a la vez, tratándolos como entradas a las redes neuronales.
Una de esas aplicaciones es para reacciones químicas, donde se desconoce la velocidad de reacción. Diferentes velocidades de reacción corresponden a diferentes soluciones y solo una solución coincide con los puntos de datos observados. Quizás le interese resolver primero un conjunto de soluciones y luego determinar las mejores velocidades de reacción (también conocidas como parámetros de ecuación). El segundo paso se conoce como problema inverso .
Aquí hay un ejemplo de cómo hacer esto usando neurodiffeq :
Digamos que tenemos una ecuación du/dt + λu = 0 y una condición inicial u(0) = U0 donde λ y U0 son constantes desconocidas. También tenemos un conjunto de observaciones t_obs y u_obs . Primero importamos BundleSolver y BundleIVP que son necesarios para obtener un paquete de solución:
desde neurodiffeq.conditions importar BundleIVPdesde neurodiffeq.solvers importar BundleSolver1Dimport matplotlib.pyplot como pltimport numpy como npimport torchdesde neurodiffeq importar diff
Determinamos el dominio de la entrada t , así como el dominio de los parámetros λ y U0 . También necesitamos tomar una decisión sobre el orden de los parámetros. Es decir, cuál debería ser el primer parámetro y cuál debería ser el segundo. Para los fines de esta demostración, elegimos λ como el primer parámetro (índice 0) y U0 como el segundo (índice 1). Es muy importante realizar un seguimiento de los índices de los parámetros.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # primer parámetro, índice = 0U0_MIN, U0_MAX = 0.2, 0.6 # segundo parámetro, índice = 1
Luego definimos las conditions y solver como de costumbre, excepto que usamos BundleIVP y BundleSolver1D en lugar de IVP y Solver1D . La interfaz de estos dos es muy similar a IVP y Solver1D . Puede obtener más información en la referencia de API.
# Los parámetros de la ecuación vienen después de las entradas (generalmente coordenadas temporales y espaciales)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# El argumento de la palabra clave debe denominarse "u_0" en BundleIVP. Si usa cualquier otra cosa, por ejemplo, `y0`, `u0`, etc., no funcionará.conditions = [BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 tiene índice 1]solver = BundleSolver1D(ode_system=diff_eq,condiciones=condiciones,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ tiene índice 0; u_0 tiene índice 1theta_max=[LAMBDA_MAX, U0_MAX], # λ tiene índice 0; u_0 tiene índice 1eq_param_index=(0,), # λ es el único; parámetro de ecuación, que tiene índice 0n_batches_valid=1,
) Dado que λ es un parámetro en la ecuación y U0 es un parámetro en la condición inicial , debemos incluir λ en diff_eq y U0 en la condición. Si un parámetro está presente tanto en la ecuación como en la condición, debe incluirse en ambos lugares. Todos los elementos de conditions pasadas a BundleSovler1D deben ser condiciones Bundle* , incluso si no tienen parámetros.
Ahora podemos entrenarlo y obtener la solución como lo haríamos normalmente.
solver.fit(max_epochs=1000)solución = solver.get_solution(mejor=Verdadero)
La solución espera tres entradas: t , λ y U0 . Todas las entradas deben tener la misma forma. Por ejemplo, si está interesado en fijar λ=4 y U0=0.4 y trazar la solución u frente a t ∈ [0,1] , puede hacer lo siguiente
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = solución(t, lmd, u0, to_numpy=True)importar matplotlib.pyplot como pltplt .plot(t,u)
Una vez que tenga una solution integrada, podrá encontrar un conjunto de parámetros (λ, U0) que coincida más estrechamente con los puntos de datos observados (t_i, u_i) . Esto se logra mediante un simple descenso de gradiente. En el siguiente ejemplo de juguete, asumimos que solo hay tres puntos de datos u(0.2) = 0.273 , u(0.5)=0.129 y u(0.8) = 0.0609 . El siguiente es el flujo de trabajo clásico de PyTorch.
# puntos de datos observadost_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# inicialización aleatoria de λ y U0; realice un seguimiento de su gradientelmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(Verdadero)], lr=1e-2)# ejecutar descenso de gradiente durante 10000 épocas para _ en rango(10000):salida = solución(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs))loss = ((salida - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, pérdida = {loss.item()}") Simple. Al importar neurodiffeq, la biblioteca detecta automáticamente si CUDA está disponible en su máquina. Dado que la biblioteca se basa en PyTorch, establecerá el tipo de tensor predeterminado en torch.cuda.DoubleTensor si se encuentra un dispositivo GPU compatible.
Consulte las secciones Redes personalizadas y Transferencia de aprendizaje.
La forma estándar de PyTorch.
Construya sus redes como se explica en Redes personalizadas: nets = [FCNN(), FCN(), ...]
Crear una instancia de un optimizador personalizado y pasarle todos los parámetros de estas redes.
parámetros = [p for net in nets for p in net.parameters()] # lista de parámetros de todas las redesMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
Pase AMBAS sus nets y su optimizer al solucionador: solver = Solver1D(..., nets=nets, optimizer=optimizer)
A diferencia de los métodos numéricos tradicionales (FEM, FVM, etc.), la solución basada en NN requiere cierto hiperajuste. La biblioteca ofrece la máxima flexibilidad para probar cualquier combinación de hiperparámetros.
Para utilizar una arquitectura de red diferente, puede pasar sus torch.nn.Module personalizados.
Para utilizar un optimizador diferente, puede pasar su propio optimizador a solver = Solver(..., optimizer=my_optim) .
Para utilizar una distribución de muestreo diferente, puede utilizar generadores integrados o escribir sus propios generadores desde cero.
Para utilizar un tamaño de muestra diferente, puede modificar los generadores o cambiar solver = Solver(..., n_batches_train) .
Para cambiar dinámicamente los hiperparámetros durante el entrenamiento, consulte nuestra función de devoluciones de llamada.
No utilice ReLU para la activación, porque su derivada de segundo orden es idénticamente 0.
Vuelva a escalar su PDE/ODE en forma adimensional, preferiblemente haga que todo esté en [0,1] . Trabajar con un dominio como [0,1000000] es propenso a fallar porque a) PyTorch inicializa los pesos de los módulos para que sean relativamente pequeños yb) la mayoría de las funciones de activación (como Sigmoid, Tanh, Swish) son más no lineales cerca de 0.
Si su PDE/ODE es demasiado complicado, considere probar el aprendizaje curricular. Comience a entrenar sus redes en un dominio más pequeño y luego amplíe gradualmente hasta cubrir todo el dominio.
Todos son bienvenidos a contribuir a este proyecto.
Al contribuir a este repositorio, consideramos el siguiente proceso:
Abra una edición para discutir el cambio que planea realizar.
Consulte las Pautas de contribución.
Realice el cambio en un repositorio bifurcado y actualice README.md si se realizan cambios en la interfaz.
Abra una solicitud de extracción.