7 funciones simples de JavaScript que le darán una idea de cómo las máquinas realmente pueden "aprender".
En otros idiomas: Русский, Português
¿También podría interesarte? Experimentos interactivos de aprendizaje automático
NanoNeuron es una versión demasiado simplificada del concepto Neuron de Neural Networks. NanoNeuron está capacitado para convertir valores de temperatura de Celsius a Fahrenheit.
El ejemplo de código de NanoNeuron.js contiene 7 funciones simples de JavaScript (que abordan la predicción del modelo, el cálculo de costos, la propagación hacia adelante/hacia atrás y el entrenamiento) que le darán una idea de cómo las máquinas realmente pueden "aprender". Sin bibliotecas de terceros, sin conjuntos de datos externos ni dependencias, solo funciones de JavaScript puras y simples.
☝?Estas funciones NO son, de ninguna manera, una guía completa para el aprendizaje automático. ¡Muchos conceptos de aprendizaje automático se omiten y se simplifican demasiado! Esta simplificación se realiza a propósito para brindarle al lector una comprensión y una sensación realmente básicas de cómo las máquinas pueden aprender y, en última instancia, hacer posible que el lector reconozca que no se trata de "MAGIA del aprendizaje automático", sino de "MATEMÁTICAS del aprendizaje automático".
Probablemente hayas oído hablar de las neuronas en el contexto de las redes neuronales. NanoNeuron es eso pero más simple y lo vamos a implementar desde cero. Por razones de simplicidad, ni siquiera vamos a construir una red con nanoneuronas. Lo tendremos todo funcionando por sí solo, haciendo algunas predicciones mágicas para nosotros. Es decir, le enseñaremos a esta NanoNeuron singular a convertir (predecir) la temperatura de Celsius a Fahrenheit.
Por cierto, la fórmula para convertir grados Celsius a Fahrenheit es la siguiente:
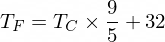
Pero por ahora nuestra NanoNeuron no lo sabe...
Implementemos nuestra función de modelo NanoNeuron. Implementa una dependencia lineal básica entre x e y que se parece y = w * x + b . Simplemente decimos que nuestra NanoNeuron es un "niño" en una "escuela" a la que se le enseña a dibujar la línea recta en coordenadas XY .
Las variables w , b son parámetros del modelo. NanoNeuron sólo conoce estos dos parámetros de la función lineal. Estos parámetros son algo que NanoNeuron va a "aprender" durante el proceso de entrenamiento.
Lo único que puede hacer NanoNeuron es imitar la dependencia lineal. En su método predict() acepta alguna entrada x y predice la salida y . No hay magia aquí.
function NanoNeuron ( w , b ) {
this . w = w ;
this . b = b ;
this . predict = ( x ) => {
return x * this . w + this . b ;
}
}(... espera... regresión lineal, ¿eres tú?) ?
El valor de la temperatura en Celsius se puede convertir a Fahrenheit usando la siguiente fórmula: f = 1.8 * c + 32 , donde c es una temperatura en Celsius y f es la temperatura calculada en Fahrenheit.
function celsiusToFahrenheit ( c ) {
const w = 1.8 ;
const b = 32 ;
const f = c * w + b ;
return f ;
} ; En última instancia, queremos enseñarle a nuestra NanoNeuron a imitar esta función (para aprender que w = 1.8 y b = 32 ) sin conocer estos parámetros de antemano.
Así es como se ve la función de conversión de Celsius a Fahrenheit:
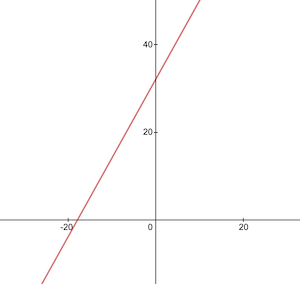
Antes del entrenamiento, necesitamos generar conjuntos de datos de entrenamiento y prueba basados en la función celsiusToFahrenheit() . Los conjuntos de datos constan de pares de valores de entrada y valores de salida correctamente etiquetados.
En la vida real, en la mayoría de los casos, estos datos se recopilarían en lugar de generarse. Por ejemplo, podríamos tener un conjunto de imágenes de números dibujados a mano y el conjunto de números correspondiente que explica qué número está escrito en cada imagen.
Usaremos datos de ejemplo de ENTRENAMIENTO para entrenar nuestra NanoNeuron. Antes de que nuestra NanoNeuron crezca y pueda tomar decisiones por sí sola, debemos enseñarle lo que está bien y lo que está mal mediante ejemplos de entrenamiento.
Usaremos ejemplos de PRUEBA para evaluar qué tan bien se desempeña nuestra NanoNeuron con los datos que no vio durante el entrenamiento. Este es el punto donde pudimos ver que nuestro "pequeño" ha crecido y puede tomar decisiones por sí solo.
function generateDataSets ( ) {
// xTrain -> [0, 1, 2, ...],
// yTrain -> [32, 33.8, 35.6, ...]
const xTrain = [ ] ;
const yTrain = [ ] ;
for ( let x = 0 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTrain . push ( x ) ;
yTrain . push ( y ) ;
}
// xTest -> [0.5, 1.5, 2.5, ...]
// yTest -> [32.9, 34.7, 36.5, ...]
const xTest = [ ] ;
const yTest = [ ] ;
// By starting from 0.5 and using the same step of 1 as we have used for training set
// we make sure that test set has different data comparing to training set.
for ( let x = 0.5 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTest . push ( x ) ;
yTest . push ( y ) ;
}
return [ xTrain , yTrain , xTest , yTest ] ;
} Necesitamos tener alguna métrica que nos muestre qué tan cerca está la predicción de nuestro modelo de los valores correctos. El cálculo del coste (el error) entre el valor de salida correcto de y y prediction que creó nuestra NanoNeuron se realizará mediante la siguiente fórmula:
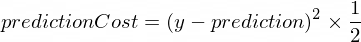
Esta es una simple diferencia entre dos valores. Cuanto más cerca estén los valores entre sí, menor será la diferencia. Estamos usando una potencia de 2 aquí solo para deshacernos de los números negativos, de modo que (1 - 2) ^ 2 sea lo mismo que (2 - 1) ^ 2 . La división por 2 se realiza solo para simplificar aún más la fórmula de propagación hacia atrás (ver más abajo).
La función de costo en este caso será tan simple como:
function predictionCost ( y , prediction ) {
return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
} Hacer propagación hacia adelante significa hacer una predicción para todos los ejemplos de entrenamiento de los conjuntos de datos xTrain e yTrain y calcular el costo promedio de esas predicciones a lo largo del camino.
En este punto, simplemente dejamos que nuestra NanoNeuron diga su opinión, permitiéndole simplemente adivinar cómo convertir la temperatura. Podría estar estúpidamente mal aquí. El coste medio nos mostrará qué tan equivocado está nuestro modelo en este momento. Este valor de costo es realmente importante ya que se cambiaron los parámetros w y b de NanoNeuron y se realizó la propagación hacia adelante nuevamente; Podremos evaluar si nuestra NanoNeuron se volvió más inteligente o no después de que estos parámetros cambien.
El coste medio se calculará mediante la siguiente fórmula:
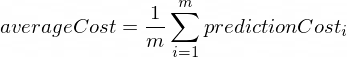
Donde m es una cantidad de ejemplos de entrenamiento (en nuestro caso: 100 ).
Así es como podemos implementarlo en código:
function forwardPropagation ( model , xTrain , yTrain ) {
const m = xTrain . length ;
const predictions = [ ] ;
let cost = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
cost += predictionCost ( yTrain [ i ] , prediction ) ;
predictions . push ( prediction ) ;
}
// We are interested in average cost.
cost /= m ;
return [ predictions , cost ] ;
}Cuando sepamos qué tan correctas o incorrectas son las predicciones de nuestra NanoNeuron (según el costo promedio en este momento), ¿qué debemos hacer para que las predicciones sean más precisas?
La propagación hacia atrás nos da la respuesta a esta pregunta. La propagación hacia atrás es el proceso de evaluar el costo de la predicción y ajustar los parámetros w y b de la NanoNeuron para que las predicciones siguientes y futuras sean más precisas.
¿Este es el lugar donde el aprendizaje automático parece mágico?♂️. El concepto clave aquí es la derivada , que muestra qué paso dar para acercarse al mínimo de la función de costos.
Recuerde, encontrar el mínimo de una función de costo es el objetivo final del proceso de capacitación. Si encontramos valores para w y b tales que nuestra función de costo promedio sea pequeña, significaría que el modelo NanoNeuron hace predicciones realmente buenas y precisas.
Los derivados son un tema amplio y separado que no cubriremos en este artículo. MathIsFun es un buen recurso para obtener una comprensión básica del mismo.
Una cosa acerca de las derivadas que te ayudará a comprender cómo funciona la propagación hacia atrás es que la derivada, por su significado, es una línea tangente a la curva de la función que apunta hacia la dirección del mínimo de la función.
Fuente de la imagen: MathIsFun
Por ejemplo, en el gráfico anterior, puedes ver que si estamos en el punto (x=2, y=4) entonces la pendiente nos dice que vayamos left y down para llegar al mínimo de la función. Fíjate también que cuanto mayor sea la pendiente, más rápido debemos desplazarnos hasta el mínimo.
Las derivadas de nuestra función averageCost para los parámetros w y b se ven así:
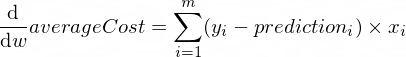
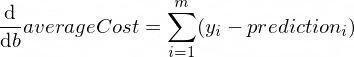
Donde m es una cantidad de ejemplos de entrenamiento (en nuestro caso: 100 ).
Puedes leer más sobre las reglas de derivadas y cómo obtener una derivada de funciones complejas aquí.
function backwardPropagation ( predictions , xTrain , yTrain ) {
const m = xTrain . length ;
// At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
// Therefore we're setting up the changing steps for each parameters to 0.
let dW = 0 ;
let dB = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
dB += yTrain [ i ] - predictions [ i ] ;
}
// We're interested in average deltas for each params.
dW /= m ;
dB /= m ;
return [ dW , dB ] ;
} Ahora sabemos cómo evaluar la exactitud de nuestro modelo para todos los ejemplos de conjuntos de entrenamiento ( propagación hacia adelante ). También sabemos cómo hacer pequeños ajustes a los parámetros w y b de nuestro modelo NanoNeuron ( propagación hacia atrás ). Pero el problema es que si ejecutamos la propagación hacia adelante y luego la propagación hacia atrás solo una vez, no será suficiente para que nuestro modelo aprenda ninguna ley/tendencia a partir de los datos de entrenamiento. Puede compararlo con asistir un día a la escuela primaria para el niño. Él/ella debe ir a la escuela no una vez sino día tras día y año tras año para aprender algo.
Por lo tanto, necesitamos repetir la propagación hacia adelante y hacia atrás de nuestro modelo muchas veces. Eso es exactamente lo que hace la función trainModel() . Es como un "maestro" para nuestro modelo NanoNeuron:
epochs ) con nuestro modelo NanoNeuron ligeramente estúpido e intentará entrenarlo/enseñarlo,xTrain e yTrain ) para el entrenamiento,alpha Algunas palabras sobre la tasa de aprendizaje alpha . Esto es sólo un multiplicador de los valores de dW y dB que hemos calculado durante la propagación hacia atrás. Entonces, la derivada nos indicó la dirección que debemos tomar para encontrar un mínimo de la función de costo (signo dW y dB ) y también nos mostró qué tan rápido debemos ir en esa dirección (valores absolutos de dW y dB ). Ahora necesitamos multiplicar esos tamaños de paso a alpha solo para ajustar nuestro movimiento al mínimo más rápido o más lento. A veces, si usamos valores grandes para alpha , es posible que simplemente saltemos el mínimo y nunca lo encontremos.
La analogía con el maestro sería que cuanto más presione a nuestro "nano-niño", más rápido aprenderá nuestro "nano-niño", pero si el maestro presiona demasiado, el "nino" tendrá un ataque de nervios y no ganará. ¿No podrás aprender nada?
Así es como vamos a actualizar los parámetros w y b de nuestro modelo:
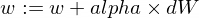
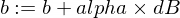
Y aquí está nuestra función de entrenador:
function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
// The is the history array of how NanoNeuron learns.
const costHistory = [ ] ;
// Let's start counting epochs.
for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
// Forward propagation.
const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
costHistory . push ( cost ) ;
// Backward propagation.
const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
// Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
nanoNeuron . w += alpha * dW ;
nanoNeuron . b += alpha * dB ;
}
return costHistory ;
}Ahora usemos las funciones que hemos creado arriba.
Creemos nuestra instancia de modelo NanoNeuron. En este momento, NanoNeuron no sabe qué valores se deben establecer para los parámetros w y b . Así que configuremos w y b al azar.
const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;Generar conjuntos de datos de entrenamiento y prueba.
const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ; Entrenemos el modelo con pequeños pasos incrementales ( 0.0005 ) durante 70000 épocas. Puedes jugar con estos parámetros, se están definiendo empíricamente.
const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;Veamos cómo fue cambiando la función de costos durante la capacitación. Esperamos que el costo después de la capacitación sea mucho menor que antes. Esto significaría que NanoNeuron se volvió más inteligente. También es posible lo contrario.
console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024 Así es como cambia el coste de la formación a lo largo de las épocas. En el eje x está el número de época x1000.
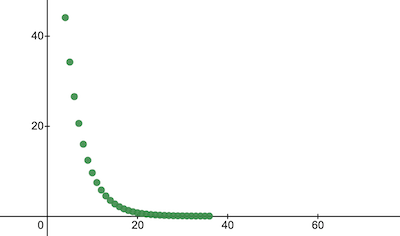
Echemos un vistazo a los parámetros de NanoNeuron para ver qué ha aprendido. Esperamos que los parámetros w y b de NanoNeuron sean similares a los que tenemos en la función celsiusToFahrenheit() ( w = 1.8 y b = 32 ) ya que nuestra NanoNeuron intentó imitarlo.
console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}Evalúe la precisión del modelo para el conjunto de datos de prueba para ver qué tan bien nuestra NanoNeuron maneja nuevas predicciones de datos desconocidos. Se espera que el costo de las predicciones en conjuntos de prueba se acerque al costo de capacitación. Esto significaría que nuestra NanoNeuron funciona bien con datos conocidos y desconocidos.
[ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023Ahora, como vemos que nuestro "niño" NanoNeuron se ha desempeñado bien en la "escuela" durante el entrenamiento y que puede convertir temperaturas de Celsius a Fahrenheit correctamente, incluso para los datos que no ha visto, podemos llamarlo "inteligente". y hazle algunas preguntas. Este fue el objetivo final de todo el proceso de formación.
const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158¡Tan cerca! Como todos los humanos, nuestra NanoNeuron es buena pero no ideal :)
¡Feliz aprendizaje para ti!
Puedes clonar el repositorio y ejecutarlo localmente:
git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuronnode ./NanoNeuron.jsLos siguientes conceptos de aprendizaje automático se omitieron y simplificaron para simplificar la explicación.
División del conjunto de datos de entrenamiento/prueba
Normalmente tienes un gran conjunto de datos. Dependiendo de la cantidad de ejemplos en ese conjunto, es posible que desees dividirlo en una proporción de 70/30 para conjuntos de entrenamiento/prueba. Los datos del conjunto deben mezclarse aleatoriamente antes de la división. Si el número de ejemplos es grande (es decir, millones), entonces la división podría ocurrir en proporciones cercanas a 90/10 o 95/5 para conjuntos de datos de entrenamiento/prueba.
La red trae el poder
Normalmente no notarás el uso de una sola neurona independiente. El poder está en la red de tales neuronas. La red podría aprender características mucho más complejas. NanoNeuron por sí sola parece más una simple regresión lineal que una red neuronal.
Normalización de entrada
Antes del entrenamiento, sería mejor normalizar los valores de entrada.
Implementación vectorizada
Para las redes, los cálculos vectorizados (matriciales) funcionan mucho más rápido que los bucles for . Normalmente, la propagación hacia adelante/hacia atrás funciona mucho más rápido si se implementa en forma vectorizada y se calcula utilizando, por ejemplo, la biblioteca Numpy Python.
Mínimo de la función de costo
La función de costos que estábamos usando en este ejemplo está demasiado simplificada. Debe tener componentes logarítmicos. Cambiar la función de costo también cambiará sus derivadas, por lo que el paso de propagación hacia atrás también usaría fórmulas diferentes.
Función de activación
Normalmente, la salida de una neurona debe pasar a través de una función de activación como Sigmoide o ReLU u otras.