Invertir matriz usando una red neuronal.
Las matrices invertidas presenta desafíos únicos para las redes neuronales, principalmente debido a las limitaciones inherentes en la realización de operaciones aritméticas precisas, como la multiplicación y la división en las activaciones. Las redes densas tradicionales a menudo necesitan ayuda con estas tareas, ya que no están diseñadas explícitamente para manejar las complejidades involucradas en la inversión de matriz. Los experimentos realizados con redes neuronales densas simples han mostrado dificultades significativas para lograr inversiones de matriz precisas. A pesar de varios intentos de optimizar el proceso de arquitectura y capacitación, los resultados a menudo necesitan mejoras. Sin embargo, la transición a una arquitectura más compleja, una red residual de 7 capas (RESNET), puede conducir a mejoras marcadas en el rendimiento.
La arquitectura de resnet, conocida por su capacidad para aprender representaciones profundas a través de conexiones residuales, ha demostrado ser efectiva para abordar la inversión de la matriz. Con millones de parámetros, esta red puede capturar patrones intrincados dentro de los datos que los modelos más simples no pueden. Sin embargo, esta complejidad tiene un costo: se requieren datos sustanciales de capacitación para una generalización efectiva.
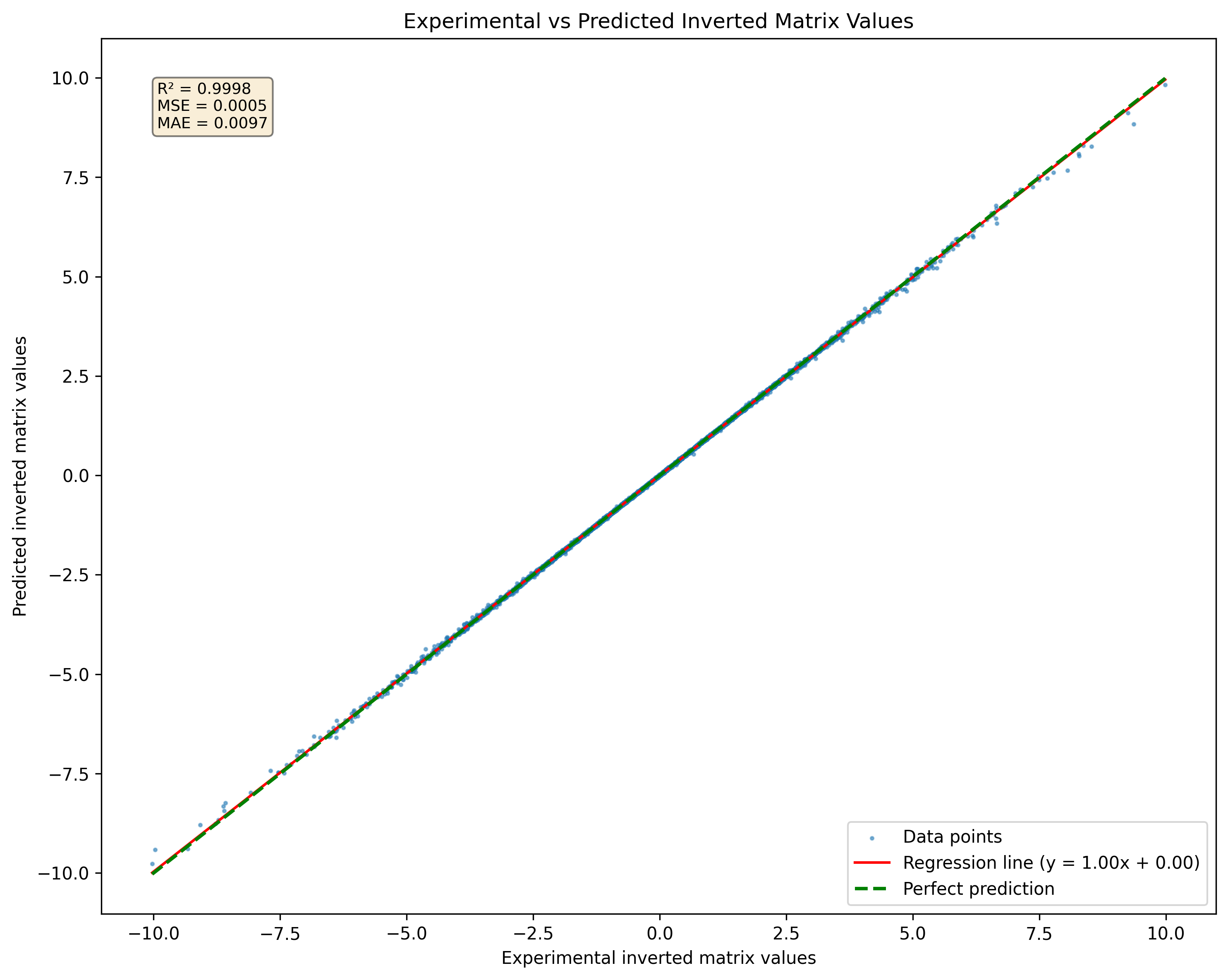Figura 1: Visualización de una red neuronal predicha matriz invertida para un conjunto de matrices 3x3 nunca vistas en el conjunto de datos
Para evaluar el rendimiento de la red neuronal en la predicción de las inversiones de matriz, se emplea una función de pérdida específica:
En esta ecuación:
El objetivo es minimizar la diferencia entre la matriz de identidad y el producto de la matriz original y su inverso predicho. Esta función de pérdida mide efectivamente qué tan cerca está el inverso predicho de ser preciso.
Además, si
Esta función de pérdida ofrece distintas ventajas sobre las funciones de pérdida tradicionales, como el error medio cuadrado (MSE) o el error absoluto medio (MAE).
Medición directa de la precisión de la inversión El objetivo principal de la inversión de la matriz es garantizar que el producto de una matriz y su inversa produce la matriz de identidad. La función de pérdida captura directamente este requisito midiendo la desviación de la matriz de identidad. En contraste, MSE y MAE se centran en las diferencias entre los valores predichos y los valores verdaderos sin abordar explícitamente la propiedad fundamental de la inversión de matriz.
Énfasis en la integridad estructural mediante el uso de una función de pérdida que evalúa cuán cerca está el producto AA -1AA - 1 a II, enfatiza el mantenimiento de la integridad estructural de las matrices involucradas. Esto es particularmente importante en las aplicaciones donde la preservación de las relaciones lineales es crucial. Las funciones de pérdida tradicionales como MSE y MAE no tienen en cuenta este aspecto estructural, lo que potencialmente conduce a soluciones que minimizan el error pero no satisfacen los requisitos matemáticos de la inversión de la matriz.
Aplicabilidad a las matrices no síntecientes Esta función de pérdida supone inherentemente que las matrices que se inverten no son singulares (es decir, invertibles). En escenarios en los que están presentes matrices singulares, las funciones de pérdida tradicionales pueden producir resultados engañosos ya que no tienen en cuenta la imposibilidad de obtener un inverso válido. La función de pérdida propuesta destaca esta limitación al producir errores más grandes al intentar invertir matrices singulares.
Una limitación significativa al usar redes neuronales para la inversión de la matriz es su incapacidad para manejar las matrices singulares de manera efectiva. Una matriz singular no tiene una inversa; Por lo tanto, cualquier intento de una red neuronal de predecir un inverso para tales matrices producirá resultados incorrectos. En la práctica, si se presenta una matriz singular durante el entrenamiento o la inferencia, la red aún puede obtener un resultado, pero esta salida no será válida o significativa. Esta limitación subraya la importancia de garantizar que los datos de capacitación consistan en matrices no singulares siempre que sea posible.
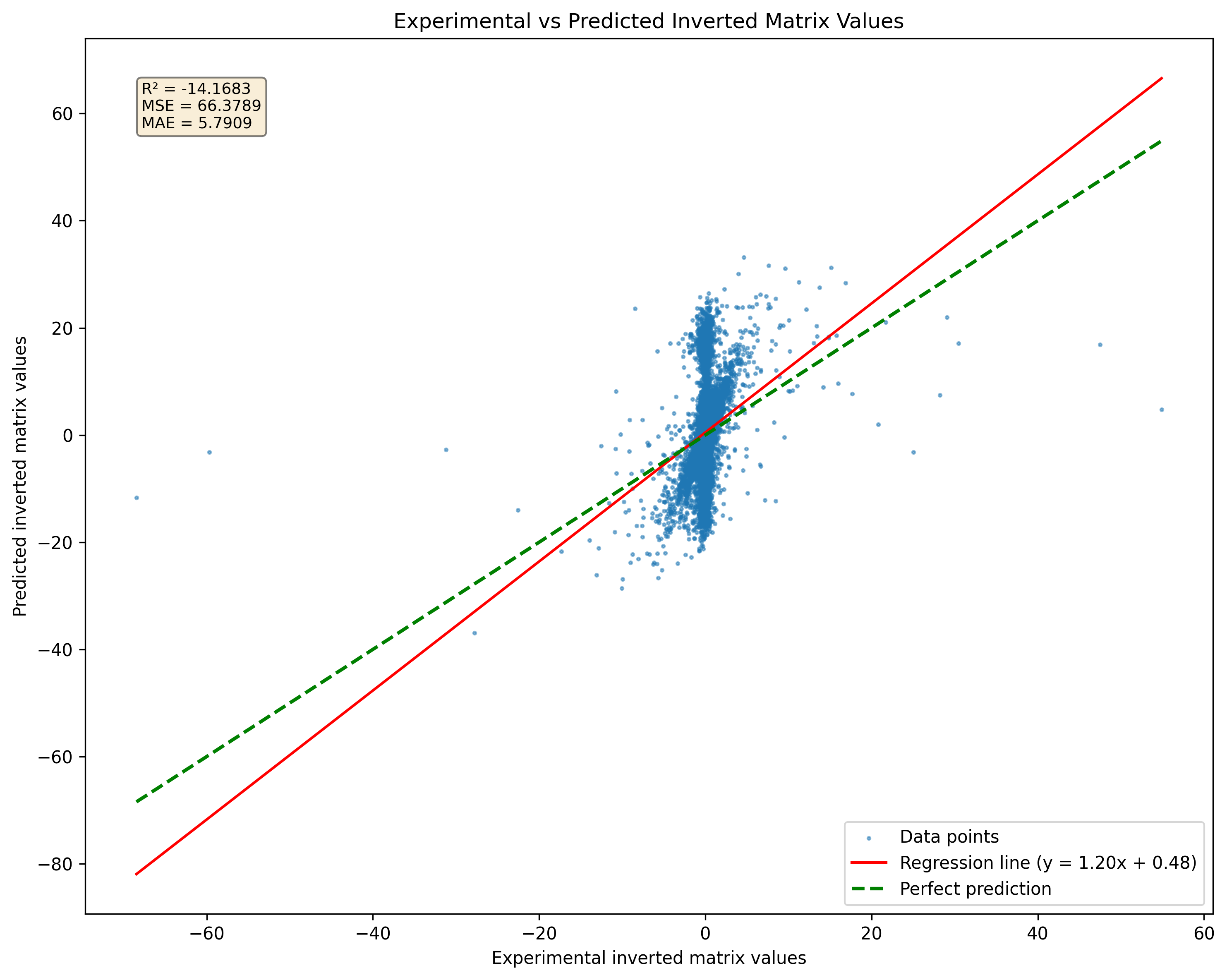Figura 2: Comparación de la predicción del modelo para matrices singulares versus pseudoinversiones. Tenga en cuenta que el modelo producirá resultados independientemente de la singularidad de la matriz.
La investigación indica que un modelo RESNET puede memorizar una buena cantidad de muestras sin una pérdida significativa de precisión. Sin embargo, aumentar el tamaño del conjunto de datos a 10 millones de muestras puede conducir a un sobreajuste severo. Este sobreajuste ocurre a pesar del gran volumen de datos, lo que resalta que simplemente aumentar el tamaño del conjunto de datos no garantiza una generalización mejorada para modelos complejos. Para abordar este desafío, se puede adoptar una estrategia continua de generación de datos. En lugar de confiar en un conjunto de datos estático, se pueden generar muestras sobre la marcha y alimentarse a la red a medida que se crean. Este enfoque, que es crucial para mitigar el sobreajuste, no solo proporciona una amplia gama de ejemplos de capacitación, sino que también garantiza que el modelo esté expuesto a un conjunto de datos en constante evolución.
En resumen, si bien la inversión de matriz es inherentemente desafiante para las redes neuronales debido a las limitaciones en las operaciones aritméticas, aprovechar las arquitecturas avanzadas como Resnet puede generar mejores resultados. Sin embargo, se debe considerar cuidadosamente los requisitos de datos y los riesgos de sobreajuste. Las muestras de entrenamiento de generación continua pueden mejorar el proceso de aprendizaje del modelo y mejorar el rendimiento en las tareas de inversión de matriz. Esta versión mantiene un tono impersonal mientras discute los desafíos y estrategias en la capacitación de redes neuronales para la inversión de matriz.
DeepMatrixInversion se distribuye bajo la licencia LGPLV3
Para saber más en detalles cómo funcionan las licencias, lea el archivo "Licencia" o vaya a "http://www.gnu.org/licenses/lgpl-3.0.html"
DeepMatrixInversion es actualmente propiedad de Giuseppe Marco Randazzo.
Para instalar el repositorio de DeepMatrixInversion, puede elegir entre usar poesía, pip o pipx a continuación son las instrucciones para ambos métodos.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Esto configurará su entorno con todos los paquetes necesarios para ejecutar DeepMatrixInversion.
Crear un entorno virtual e instalar DeppMatrixInversion con PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Si prefiere usar PIPX, que le permite instalar aplicaciones de Python en entornos aislados, siga estos pasos:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
Pipx install git+https: //github.com/gmrandazzo/deepmatrixInversion.git
Para entrenar un modelo que pueda realizar la inversión de matriz, usará el comando dmxtrain. Este comando le permite especificar varios parámetros que controlan el proceso de entrenamiento, como el tamaño de las matrices, el rango de valores y la duración del entrenamiento.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
Una vez que haya capacitado a su modelo, puede usarlo para realizar la inversión de matriz en nuevas matrices de entrada. El comando de inferencia es dmxinvert, que toma una matriz de entrada y genera su inverso.
ADVERTENCIA: DMXInvert puede invertir una matriz más grande que la utilizada para entrenar el modelo a través de la fórmula de inversión de bloque de matriz Sherman-Morrison-Woodbury. Esta característica funciona solo con matrices cuyo tamaño de bloque puede dividirse por el tamaño del bloque de entrenamiento modelo sin recordatorio. La característica es altamente experimental y puede necesitar ser revisada.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Generación de un conjunto de datos artificial con matriz de entrada y salida invertida se realiza Truty DMX DMXDataSetGenerator
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Esto generará 10 matrices de tamaño 3x3 con números en un rango de -1 a +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Entonces el conjunto de datos se puede validar utilizando dmxdataSetverify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
El archivo de matriz de entrada debe formatearse de la siguiente manera:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Cada bloque de números representa una matriz separada seguida de un marcador final que indica el final de esa matriz.
