Rubik's Cube Solucione para cubos muy grandes.
Resuelve cualquier cubo de cualquier tamaño de 1 a 65536. El código se puede modificar fácilmente para manejar cubos incluso más grandes. Sin embargo, la limitación principal es la cantidad de memoria en un sistema y el tiempo que lleva resolver. El tiempo de resolución crece ~ n^2, lo que significa que lleva 4-5 veces más tiempo resolver un cubo que es 2 veces más grande en cada dimensión.
Un cubo de 1024 capas se puede resolver en aproximadamente 1,5 segundos. Un cubo de 16384 en capas se puede resolver en unos 20 minutos.
YouTube: Resolver 65536 capas YouTube: Resolver 32768 capas
Imagen de la cara delantera de un cubo 32768
Resuelve los centros y luego los bordes
Los centros se resuelven en 15 etapas donde cada etapa mueve todas las piezas de cierto color de una cara a la cara deseada. Por ejemplo: un escenario mueve todas las piezas verdes en la cara blanca hacia la cara verde. Repita esto para todos los colores y caras.
El solucionador utiliza el conmutador descrito aquí, que puede viajar a las piezas centrales desde un cuadrante de una cara hasta un demonio en otra cara. Una propiedad muy importante de este conmutador es que se puede modificar para mover muchas piezas en una sola fila al mismo tiempo. Para cubos muy grandes, esto significa que puede mover cientos, si no miles de piezas, en una sola operación. El número promedio de movimientos k = (2 * p + 5) / p donde p es el número de piezas que se pueden mover por operación. K se acerca rápidamente a 2 a medida que aumenta el tamaño del cubo.
Las esquinas se resuelven utilizando un método básico de fuerza bruta para mover la esquina en su lugar y luego girar hasta que las caras estuvieran orientadas correctamente. Will Smith puede explicar: https://www.youtube.com/watch?v=wbzkdrc9vqs
Los bordes se resuelven moviendo cada par de bordes a la cara delantera, luego cambian las piezas deseadas desde el borde izquierdo hasta el borde derecho. Una serie de funciones donde necesaria para solucionar o prevenir problemas de paridad.
Las rotaciones de la cara son esencialmente gratuitas. En lugar de mover todas las piezas en una cara dada (n^2 piezas) para realizar una rotación, el solucionador simplemente cambia el sistema de coordenadas que se usa para leer/escribir en la cara. Esto ahorra una enorme cantidad de intercambio de datos.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}Este código incluye un exportador de imagen simple que se usa representa cada cara en una imagen.
https://www.nayuki.io/page/tiny-png-output
https://github.com/nayuki/nayuki-web-publisised-code
Tiny PNG Output es una pequeña biblioteca independiente, disponible en C y C ++, que toma RGB8.8.8 píxeles y escribe un archivo PNG.
El número total de movimientos se puede estimar utilizando una fórmula simple. Suponiendo que el cubo sea suficientemente aleatorio, podemos esperar que la primera cara se resuelva 1/6 y, por lo tanto, 5/6 de las piezas tendrán que moverse. La segunda cara estará resuelta 1/5 y requerirá que se muevan 4/5 de las piezas. La tercera cara 3/4, cuarta cara 2/3, quinta cara 1/2 y la última cara se resolverá por completo. El número promedio de movimientos (k) para mover una sola pieza se puede estimar experimentalmente como ~ 2.1. El valor de K disminuye a medida que aumenta el tamaño del cubo. El valor nunca puede ser inferior a 2 ya que el conmutador requiere que cada pieza se mueva al menos 2 veces.
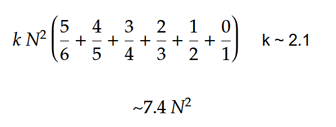
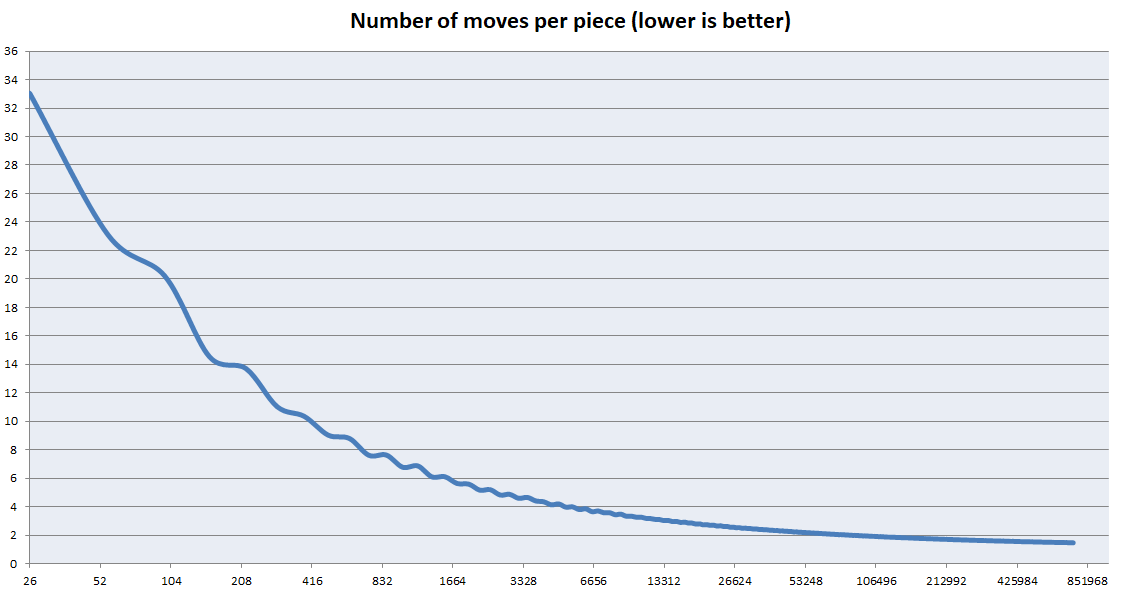
Este algoritmo está optimizado para cubos muy grandes. Sin embargo, es terrible para los cubos pequeños. Las optimizaciones principales se centraron en resolver los centros lo más rápido posible y no se consideró ninguna consideración para resolver los bordes. Sin embargo, el tamaño de los bordes es insignificante en comparación con los centros a medida que aumenta el tamaño del cubo. El siguiente gráfico muestra cómo disminuye el número promedio de movimientos por pieza con cubos más grandes. Nota: Este no es un gráfico de k. Es un gráfico de (movimientos totales) / (número de piezas)
cmake -B build -S .
cd build
cmake --build .
RCube/RCube