Este es un pequeño programa que analiza una grabación de un reloj o reloj y le dice qué tan lento o rápido se ejecuta. Puede usar esto para regular un reloj mecánico utilizando, por ejemplo, un teléfono celular para grabar su marcado.
$ Python Fourier.py Recording.wav suposición inicial: 6.0 p/m 0.00606 Hz Supongo actualizado: 5.9998549 P/m 1.88e-05 Hz El error es -2.1 segundos / día
El archivo recording.wav debe ser un archivo de sonido mono. Mi teléfono celular tiene un programa de "memorando de voz" que registra audio utilizando el micrófono incorporado. Es bastante sensible para este propósito.
Con una grabación de buena calidad, verás algo como esto:
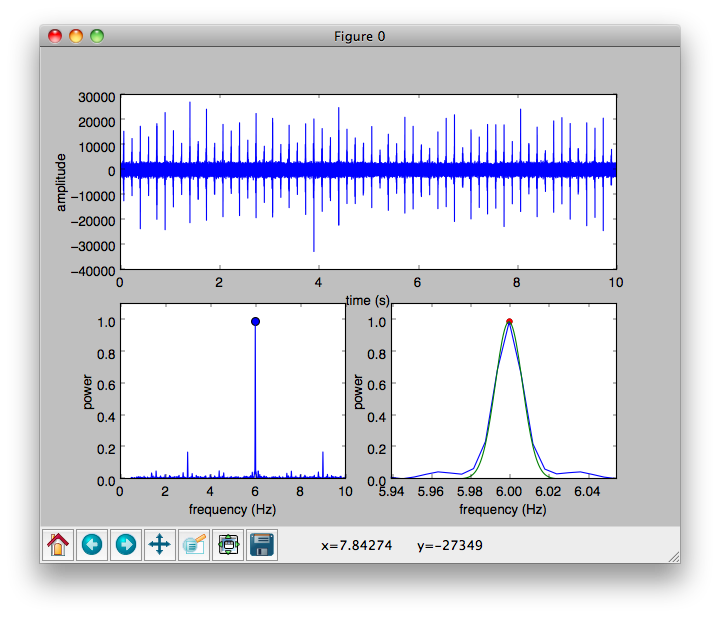
El panel superior muestra los últimos 10 segundos en la grabación ... esto le permite evaluar la calidad de sus datos. Aquí, puede ver claramente las garrapatas individuales, y que este reloj marca 6 veces por segundo. La relación señal / ruido es probablemente 10 más o menos en este ejemplo.
La trama inferior izquierda muestra la transformación de Fourier de la grabación, ampliada al rango de 0.5-10 Hz. El pico en esta parcela corresponde a la frecuencia de garrapata del reloj. Está cerca de 6 tics/por segundo, donde debería estar ... pero ¿qué tan cerca?
La gráfica inferior derecha muestra un ajuste en el pico, utilizado para estimar la frecuencia a alta precisión. Esta precisión coincide fácilmente con la estabilidad de frecuencia de un reloj mecánico (que varía ligeramente debido a las diferencias en la temperatura y la orientación, entre otras cosas).
Con una grabación (muy) de baja calidad, verá algo como esto:
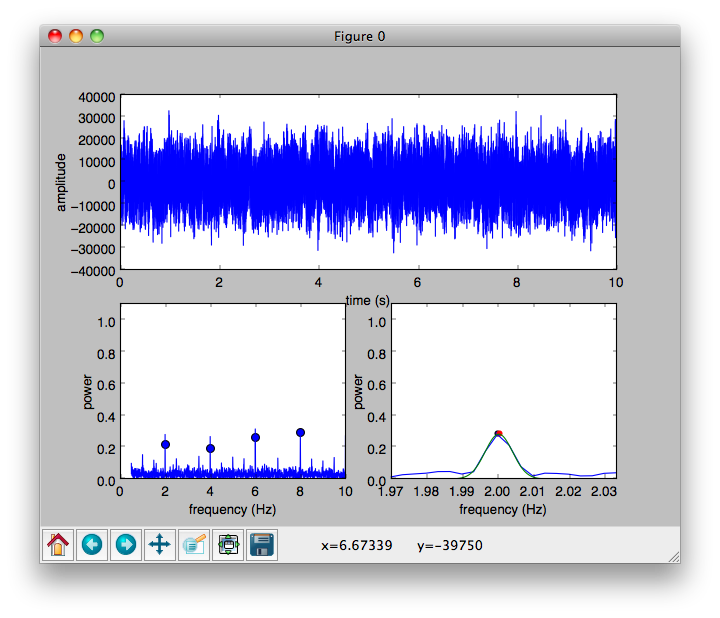
Aquí, las garrapatas individuales están enterradas en el ruido ... ¡pero el programa aún las escoge! Sin embargo, necesita una grabación más larga para alcanzar el mismo nivel de precisión.
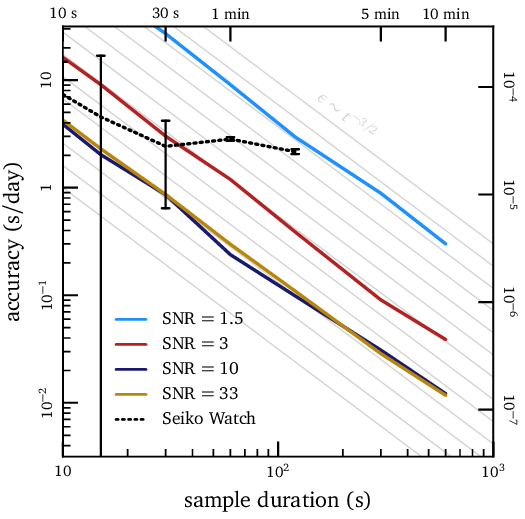
He probado el programa utilizando señales sintéticas generadas un par de formas diferentes. Los resultados se resumen en la gráfica anterior.
La incertidumbre fraccional en las escalas de medición cae con la longitud de la grabación a la potencia (3/2). También depende de la calidad de su medición. Por lo tanto, si bien desea hacer una grabación lo más buena posible, puede ser más fácil compensar la calidad con la cantidad. Encuentro que 5 minutos de datos de mierda son casi 30 segundos de datos perfectos. Pero dejar su reloj y teléfono solo en un cajón de calcetines durante 5 minutos es mucho más fácil que salir y comprar un mejor micrófono. Entonces depende de ti.
Sin embargo, si los datos son tan malos que ni siquiera puede escuchar garrapatas en la grabación, puede estar en problemas. Inténtelo de nuevo en un lugar más tranquilo o encuentre un mejor micrófono. (Y, por supuesto, asegúrese de que su reloj realmente funcione).
La línea negra punteada muestra medidas de un reloj real. Quería ajustarlo para correr con unos segundos por día y encontré que una grabación de 30 segundos o un minuto era adecuada para la tarea. Empuje la barra del regulador, grabas por un minuto, empujas nuevamente, y así sucesivamente hasta que obtienes una respuesta con la que estás contento. Lo regulé en aproximadamente 2 segundos por día, que era mi objetivo. Eso se traduce en un error de menos de una centésima de una garrapata en el lapso de la grabación, lo cual es bastante impresionante, ¡creo!
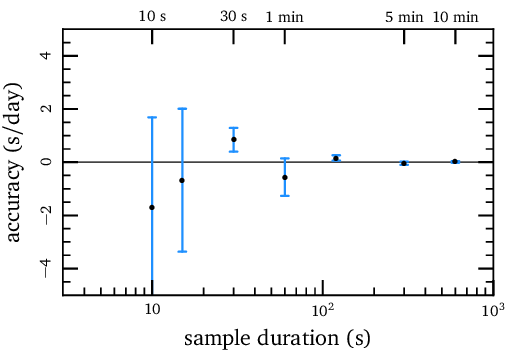
La gráfica anterior muestra una prueba utilizando una señal 'tick' sintética generada usando Audacity. Esto muestra que la incertidumbre informada por el programa es una representación bastante significativa de la verdadera incertidumbre "1-σ".
El código es bastante sencillo, y la mayor parte del esfuerzo se hizo para hacerlo funcionar previsiblemente sin ninguna intervención humana. I Fourier transforma la señal de entrada para medir la frecuencia máxima. Antes de transformar, presiono la señal con una ventana gaussiana ... elijo la forma de la ventana de modo que los picos de frecuencia tendrán una forma gaussiana con un ancho de ~ 3 contenedores de frecuencia. Esto se puede ajustar con precisión con un perfil gaussiano, produciendo una buena estimación de la verdadera frecuencia. Puede mirar las tramas para tener una idea de qué tan bien está funcionando.
Utilizo una función Scipy para identificar automáticamente los picos, lo que parece funcionar bastante bien.
E intento identificar una longitud "óptima" para el FFT. No hay problemas con eso hasta ahora.
Los resultados no son sensibles a la frecuencia de muestreo, a menos que sea demasiado bajo para resolver adecuadamente el sonido de "tictac" del reloj. Pero el programa funciona bastante rápido, por lo que no hay razón para no usar la tasa de muestreo de 44.1 kHz que es bastante estándar.