
y las tareas de Fiber en React, y las diferentes tareas de Fiber tienen diferentes prioridades. React necesita procesar primero las tareas con alta prioridad. Por ejemplo, los clics y las entradas del usuario son tareas de alta prioridad, porque las operaciones del usuario definitivamente esperan tener efectos inmediatos para mejorar la experiencia del usuario. Por ejemplo, la prioridad de los eventos de animación debe ser menor. Después de que una nueva tarea de alta prioridad ingresa a la cola, React debe procesarla primero.
Para almacenar estas tareas, hay dos grupos de tareas en React.
// Las tareas se almacenan en un montón mínimo var tareaQueue = []; var timerQueue = [];
taskQueue y timerQueue son matrices. El primero almacena tareas que se ejecutarán inmediatamente, mientras que el segundo almacena tareas que pueden retrasarse.
var nueva tarea = {
id: taskIdCounter++, // Marcar id de tarea
devolución de llamada, // función de devolución de llamada prioridadLevel, // prioridad de la tarea startTime, // hora de inicio de la tarea, punto de tiempo expirationTime, // tiempo de vencimiento, punto de tiempo sortIndex: -1, // clasificación de tareas, el valor proviene del tiempo de vencimiento, entonces el valor Cuanto menor sea el valor, mayor será la prioridad}; Una vez que llega una nueva tarea a React, primero usará currentTime para registrar la hora actual (rendimiento.now() o Date.now()). parámetro de retraso, entonces la tarea comienza a ejecutarse tiempo de inicio = tiempo actual + retraso;. A continuación, si se establece startTime> currentTime, demuestra que la tarea se puede posponer, luego la tarea ingresa a timerQueue; de lo contrario, ingresa a taskQueue.
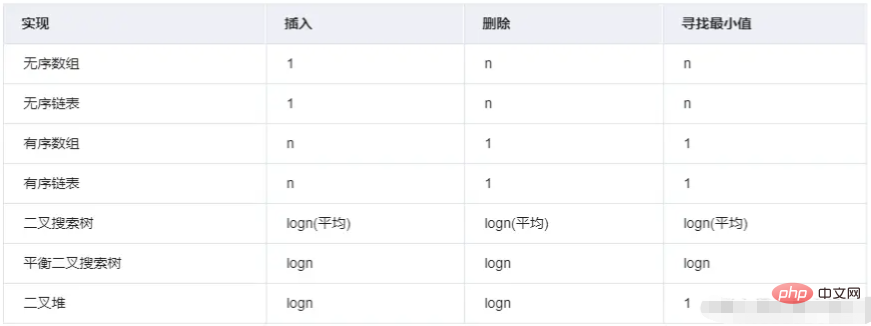
¿Cómo encuentra React la tarea con la mayor prioridad? Tome taskQueue como ejemplo. Es un grupo de tareas dinámico (cola de tareas) y el formulario de datos es una matriz. Por supuesto, puede ordenar según la prioridad, es decir, Array.sort Cuando se agrega una nueva tarea a la cola, se clasifica primero y luego se encuentra y ejecuta la tarea con la mayor prioridad. Pero la complejidad temporal promedio de Array.sort es O (nlogn), que no es la mejor solución.
SortIndex se utiliza para ordenar en la nueva Tarea de taskQueue. Este valor se toma del tiempo de vencimiento, lo que significa que cuanto mayor sea la prioridad de la tarea, más será necesario comprenderla y ejecutarla, por lo que el tiempo de vencimiento será menor. Cuanto mayor sea la prioridad, más pequeño será el tiempo de vencimiento. Cuanto menor sea el tiempo, más pequeño será naturalmente el índice de clasificación. De hecho, esta es una cola prioritaria .
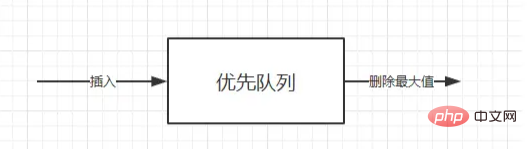
La cola de prioridad también es un tipo de cola ( en primer lugar, es una cola y, en segundo lugar, la cola entra, la primera en salir ). La única diferencia es que el orden de salida de la cola de prioridad se basa en la prioridad en algunos casos; , es posible que necesite encontrar El elemento mínimo o máximo en el conjunto de elementos se puede operar utilizando la cola de prioridad ADT. La cola de prioridad ADT es una estructura de datos que admite operaciones de inserción y eliminación de valor mínimo (devolver y eliminar el elemento mínimo) o. operación de eliminación del valor máximo (devolver y eliminar el elemento mínimo elimina el elemento más grande).
Si el elemento con el valor clave más pequeño tiene la prioridad más alta, entonces esta cola de prioridad se denomina cola de prioridad ascendente (es decir, el elemento más pequeño siempre se elimina primero). De manera similar, si el elemento con el valor clave más grande tiene la prioridad más alta, entonces este tipo de cola de prioridad se llama cola de prioridad descendente (es decir, el elemento más grande siempre se elimina primero, ya que estos dos tipos son simétricos, solo es necesario); para centrarse en uno de ellos, como la cola de prioridad ascendente.
Por ejemplo : cuando estábamos comprando boletos, todos estábamos haciendo cola y tenía la misma prioridad. El que estaba al frente de la cola compraría el boleto primero, pero luego vino un soldado y tenía mayor prioridad y estaba directamente en la cola. El frente.
El montón mínimo (montón raíz pequeño, montón superior pequeño...) se utiliza en React para lograr esta función. Es decir, convertir taskQueue en un montón mínimo, luego sacar la tarea superior para su ejecución, acumular taskQueue y mantenerla como una estructura de datos de montón mínimo. Al insertar una nueva tarea en taskQueue, también se debe acumular y mantenerla siempre como un montón mínimo.
: En algunos lugares, el montón se llama cola de prioridad (no es exacto. En primer lugar, es una cola y tiene las características de una cola, es decir, " primero en entrar, primero en salir "). . En segundo lugar, los elementos de esta cola tienen prioridades y aquellos con mayores prioridades ocuparán el primer lugar.
Para ser precisos, un montón es una forma de implementar una cola de prioridad. Por supuesto, las colas prioritarias también se pueden implementar de otras formas.
Dijimos antes que la clasificación del montón es una clasificación inestable, pero taskQueue espera que este proceso sea estable. Es decir, si es posible que el tiempo de vencimiento de dos tareas sea el mismo, entonces depende de quién ingresa. Primero, el grupo de tareas es el valor de la identificación de newTask. Cada vez que llega una nueva tarea, la identificación aumentará en 1.
función comparar (a, b) {
// Compara primero el índice de clasificación y luego el ID de la tarea.
diferencia constante = a.sortIndex - b.sortIndex;
devolver diferencia! == 0? diferencia: a.id - b.id;
} Antes de comprender el montón mínimo, revisemos los conocimientos básicos.
se refiere a un árbol ordenado en el que el grado de los nodos del árbol no es mayor que 2. Es el árbol más simple e importante.
es un árbol binario en el que todos los nodos de cada nivel tienen dos nodos secundarios, excepto el último nivel que no tiene ningún nodo secundario.
Desde una perspectiva gráfica, un árbol binario completo parece un triángulo.
Si el número de niveles de un árbol binario es K y el número total de nodos es (2^k) -1, entonces es un árbol binario completo.
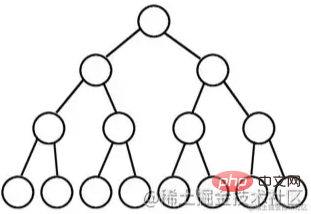
Un árbol binario completo significa "las hijas tienen ambos lados" y es muy perfecto, por eso se le llama árbol binario completo.
excluyendo los nodos hoja, el grado de todos los nodos es 2. En otras palabras, el grado de todos los nodos sólo puede ser 0 o 2.
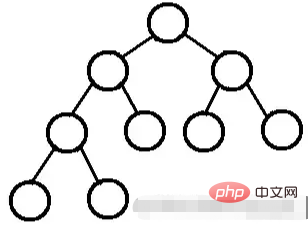
Un árbol binario perfecto no tiene hijos o tiene ambos hijos.
El texto original en inglés del árbol binario completo:
Un árbol binario completo (FBT) es un árbol en el que cada nodo excepto las hojas tiene dos hijos.
El texto original en inglés del árbol binario perfecto:
Un árbol binario perfecto (PBT) es un árbol con todos los nodos de las hojas a la misma profundidad. Todos los nodos internos tienen grado 2.
Todos los libros extranjeros hacen referencia a los primeros libros de texto traducidos sobre árboles binarios completos y árboles binarios perfectos, pero los primeros artículos traducidos están mal traducidos. Ahora en China, sólo podemos cometer errores cuando están equivocados (todo el mundo está equivocado, entonces el equivocado también tiene razón. Por ejemplo, los lobbystas...). Si quieres discutir estos dos conceptos con amigos extranjeros, debes prestar atención.
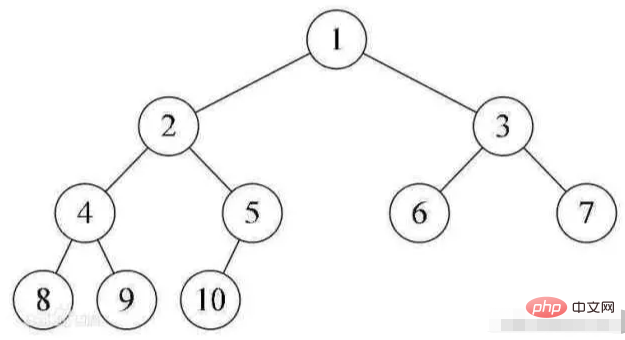
Un árbol binario(CBT) es un árbol binario en el que cada nivel, excepto posiblemente el último, está completamente lleno y todos los nodos están lo más a la izquierda posible.
Un árbol binario con n nodos de profundidad k, numera los nodos en el. árbol de arriba a abajo y de izquierda a derecha. Si el nodo numerado i (1≤i≤n) está en el árbol binario con el nodo numerado i en el árbol binario completo, si las posiciones son las mismas, el árbol binario es. llamado árbol binario completo.
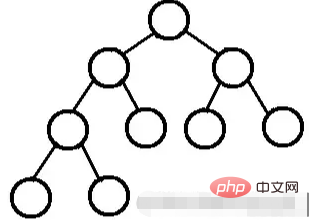
El montón siempre satisface las siguientes propiedades:
primero debemos comprender el montón raíz grande y
;el montón raíz pequeño En un árbol binario completo Todos los nodos son más grandes (o más pequeños) que sus nodos secundarios, por lo que aquí hay dos situaciones, el montón máximo y el montón mínimo.
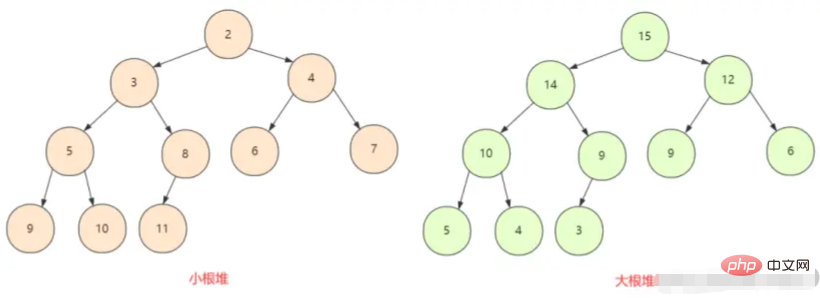
El montón suele ser una matriz de objetos que puede verse como un árbol binario completo . Por supuesto, los árboles binarios también se pueden representar mediante matrices.
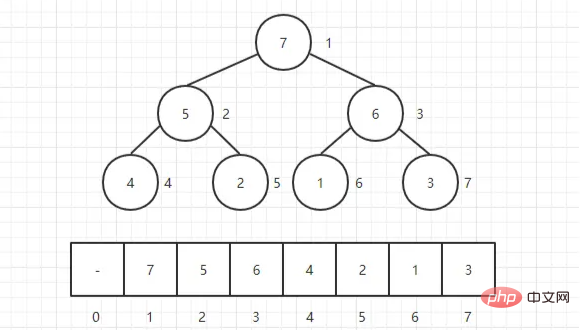
es construir el montón primero y luego ajustarlo.
, para un árbol binario (representación de matriz), ajustamos de abajo hacia arriba, comenzando desde el "primer nodo que no es hoja" y ajustando hacia adelante. Las reglas de ajuste son las siguientes:
Construir un montón es O (n). ) proceso de complejidad temporal.
① Comience desde el primer nodo no hoja para juzgar el intercambio hacia abajo (shiftDown), de modo que el nodo actual y el hijo puedan mantener las propiedades del montón
. ② Sin embargo, el reemplazo normal de nodos puede no ser un problema si el intercambio rompe las propiedades de la estructura del montón. del niño, entonces debe ser re- ShiftDown el nodo intercambiado hasta que se detenga.
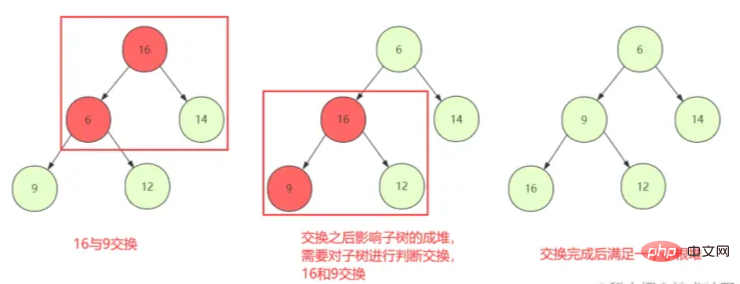
la estructura del montón
Destruya la estructura del montón.
① Simplemente coloque el último elemento primero. De esta manera, solo necesita juzgar el desplazamiento de intercambio (shiftDown), pero debe tener en cuenta que el tamaño de todo el montón ha cambiado en este momento. Lógicamente, no usaremos la posición descartada, por lo que debemos incluir un montón. parámetro de tamaño al diseñar la función.
② Repita la operación anterior hasta obtener todos los elementos del montón.
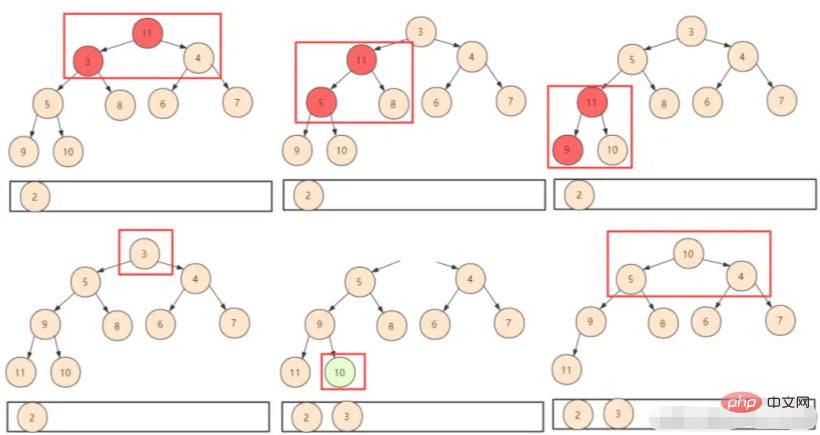
En términos del análisis de la complejidad del algoritmo del montón, la complejidad del tiempo de construcción del montón anterior era O (n). Cada vez que se elimina la parte superior del montón y luego se intercambia hacia abajo, se registra el número de cada uno. De esta manera, la complejidad es O (nlogn) y la complejidad del tiempo total es O (n) + O (nlogn) = O (nlogn).
Heap es adecuado para mantener el valor máximo de la colección.
Después de que un elemento sale del montón, el costo de reajustarlo para obtener el elemento superior del montón (es decir, el segundo valor más alto) es relativamente bajo, porque después de que el elemento sale, el montón es un semi -producto terminado, y el segundo valor más alto se obtiene de un producto semiacabado. Por supuesto, el costo es relativamente bajo y la complejidad del tiempo es O (logn), pero si se recorre una vez para encontrar el segundo valor más alto, la complejidad del tiempo es O (n).
código de implementación del código está escrito en Javascript ES6.
montón de clase{
constructor(datos, comp) {
this.data = datos? datos: [];
// Reglas de comparación: más flexibles, puedes comparar valores u objetos this.compartor = comp ? comp : (ab) => ab;
// Ajustar al montón (cola de prioridad)
this.heapify();
}
amontonar() {
if(this.size() <= 1) retorno;
// Comience a ajustar desde el primer nodo que no es hoja, o puede ajustar desde el último elemento for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Ajustar el montón. El ajuste hacia abajo también se puede implementar mediante recursividad. Aquí, la iteración se utiliza para implementar this.shiftDown(i);
}
}
// Ajustar shiftDown(i) {
deja izquierda = 2*i +1;
vamos a la derecha = 2*i +2;
let len = this.size();
mientras(yo <len) {
let findIndex = i;
//El niño izquierdo es "más grande"
if(izquierda < len && this.compartor(this.data[izquierda], this.data[findIndex]) < 0) {
findIndex = izquierda;
}
// El niño correcto es "más grande"
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = correcto;
}
si (yo! == buscar índice) {
// Intercambiar el nodo actual con un valor mayor [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// Después de ajustar esta capa, puede afectar las características del montón de la capa inferior, así que continúe ajustando la capa inferior (implementación iterativa o recursiva)
i = buscarIndice;
izquierda = 2*i +1;
derecha = 2*i +2;
}
demás {
// Si no es necesario ningún ajuste, salta (debe saltar, de lo contrario el ciclo no puede finalizar)
romper;
}
}
}
// Ajustar shiftUp(i){ hacia arriba
// Encuentra el subíndice de parent let parentIndex = Math.floor((i-1)/2);
// Ajusta el máximo a 0
mientras(índicepadre >=0 ) {
let findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = índicepadre;
}
if(buscaríndice!== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = buscarIndice;
parentIndex = Math.floor((i-1)/2);
}
demás {
romper;
}
}
}
// Obtener el número de todos los elementos en el tamaño del montón(){
devolver esta.longitud.de.datos;
}
// Obtener el primer elemento del montón peek(){
if(!this.size()) devuelve nulo;
devolver this.data[0];
}
//Añadir un elemento al montón push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Extrae el primer elemento del montón pop(){
if(!this.size()) devuelve nulo;
let res = this.data[0];
si(este.tamaño() == 1) {
this.data.pop();
}
demás {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
devolver resolución;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
sea comp = (a, b) => ab;
let montón = nuevo montón(arr, comp);
deja res = [];
while(montón.tamaño()) {
res.push(montón.pop());
}
console.log(res); el elemento en arr también puede ser un objeto.
El directorio paquetes/programador en el código fuente de React es el código relacionado con el módulo de programación de tareas de React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. y sus afiliados.
*
* Este código fuente tiene la licencia MIT que se encuentra en el
* Archivo de LICENCIA en el directorio raíz de este árbol fuente.
*
* @flujo estricto
*/
escriba Montón = Matriz<Nodo>;
tipo Nodo = {|
identificación: número,
sortIndex: número,
|};
función de exportación push(montón: Montón, nodo: Nodo): void {
índice constante = montón.longitud;
montón.push(nodo);
tamizar(montón, nodo, índice);
}
vista previa de la función de exportación (montón: montón): nodo | nulo {
const primero = montón[0];
devolver primero === indefinido? nulo: primero;
}
función de exportación pop (montón: Montón): Nodo | nulo {
const primero = montón[0];
si (primero! == indefinido) {
const último = montón.pop();
si (¡último! == primero) {
montón[0] = último;
tamizar(montón, último, 0);
}
regresar primero;
} demás {
devolver nulo;
}
}
función tamizar(montón, nodo, i) {
sea índice = i;
mientras (verdadero) {
const parentIndex = (índice - 1) >>> 1;
const padre = montón[parentIndex];
if (padre! == indefinido && comparar (padre, nodo) > 0) {
// El padre es más grande. Intercambia posiciones.
montón[parentIndex] = nodo;
montón[índice] = padre;
índice = índicepadre;
} demás {
// El padre es más pequeño.
devolver;
}
}
}
función tamizar(montón, nodo, i) {
sea índice = i;
longitud constante = montón.longitud;
mientras (índice <longitud) {
const índiceizquierdo = (índice + 1) * 2 - 1;
const izquierda = montón[leftIndex];
const índicederecho = índiceizquierdo + 1;
const derecha = montón[rightIndex];
// Si el nodo izquierdo o derecho es más pequeño, intercambie con el más pequeño de ellos.
if (izquierda! == indefinido && comparar (izquierda, nodo) <0) {
if (derecha! == indefinido && comparar (derecha, izquierda) <0) {
montón[índice] = derecho;
montón[rightIndex] = nodo;
índice = índice derecho;
} demás {
montón[índice] = izquierda;
montón[leftIndex] = nodo;
índice = índiceizquierdo;
}
} else if (derecha! == indefinido && comparar(derecha, nodo) <0) {
montón[índice] = derecho;
montón[rightIndex] = nodo;
índice = índice derecho;
} demás {
// Ninguno de los niños es más pequeño.
devolver;
}
}
}
función comparar (a, b) {
// Compara primero el índice de clasificación y luego el ID de la tarea.
diferencia constante = a.sortIndex - b.sortIndex;
devolver diferencia! == 0? diferencia: a.id - b.id;
} El montón mínimo que implementamos es ligeramente diferente de la implementación en React, pero la idea es la misma, solo que el código está escrito de manera diferente.
la programación de tareas en React se implementa utilizando el montón mínimo. Si antes tenemos una cierta comprensión del montón mínimo, aprenderemos este contenido más rápido. Personalmente, creo que es importante acumular conocimientos en la etapa inicial, pero este proceso puede resultar aburrido. En este momento, ¿cree que conoce algunos algoritmos? De hecho, estos algoritmos son de nivel básico y ni siquiera ha comenzado. Porque en el escenario de programación de tareas de React, los requisitos a implementar son muy claros, y las estructuras de datos y algoritmos a utilizar también lo son. En algunos escenarios reales, conocemos los requisitos específicos, pero no sabemos qué resultados de datos y algoritmos utilizar. Necesitamos abstraer los requisitos y diseñar estructuras de datos y algoritmos específicos basados en el modelo de datos abstracto. .