Los modelos de lenguajes grandes (LLM) han demostrado capacidades sorprendentes en muchos campos. Sin embargo, un estudio más reciente ha revelado sus "extrañas" debilidades en el razonamiento aritmético: ¡estas IA "geniales" frecuentemente cometen errores en operaciones matemáticas simples! Los investigadores realizaron un análisis en profundidad de múltiples LLM como Llama3, Pythia y GPT-J y descubrieron que no dependían de algoritmos potentes o memoria para los cálculos, sino que adoptaban una estrategia de "mezcolanza heurística", al igual que una estrategia que se basa en sobre "poca inteligencia" y "Reglas generales" para estudiantes que obtienen respuestas.
Recientemente, los modelos de lenguaje grande de IA (LLM) han funcionado bien en diversas tareas, incluida la escritura de poesía, la escritura de códigos y el chat. ¡Son simplemente omnipotentes! Pero, ¿puedes creerlo? ¡Estas IA "geniales" son en realidad "novatos en matemáticas"! A menudo se vuelcan al resolver problemas aritméticos simples, lo cual es sorprendente.
Un estudio más reciente ha revelado el "extraño" secreto detrás de las capacidades de razonamiento aritmético de LLM: no dependen de algoritmos potentes ni de la memoria, sino que adoptan una estrategia llamada "mezcolanza heurística". ¡Esto es como un estudiante que no estudia fórmulas y teoremas matemáticos en serio! pero depende de un poco de "un poco de inteligencia" y "reglas generales" para obtener la respuesta.
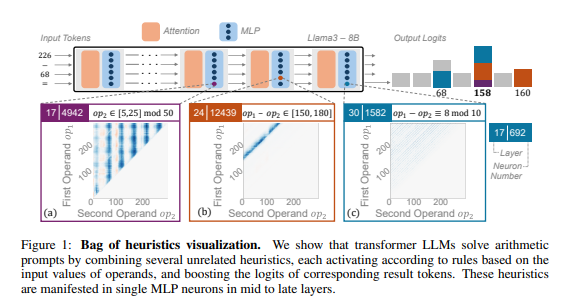
Los investigadores utilizaron el razonamiento aritmético como una tarea típica y realizaron un análisis en profundidad de múltiples LLM como Llama3, Pythia y GPT-J. Descubrieron que la parte del modelo LLM responsable de los cálculos aritméticos (llamado "circuito") está compuesta por muchas neuronas individuales, cada una de las cuales actúa como una "calculadora en miniatura" y solo es responsable de reconocer patrones numéricos específicos y generar los correspondientes. respuesta. Por ejemplo, una neurona podría ser responsable de identificar "números cuyo único dígito es 8", mientras que otra neurona podría ser responsable de identificar "operaciones de resta cuyos resultados estén entre 150 y 180".
Estas "microcalculadoras" son como un revoltijo de herramientas y, en lugar de utilizarlas según un algoritmo específico, LLM utiliza una combinación aleatoria de estas "herramientas" para calcular una respuesta basada en el patrón de números que ingresa. Es como un chef que no tiene una receta fija, sino que la mezcla a su antojo según los ingredientes que tiene a mano y finalmente hace una "cocina oscura".
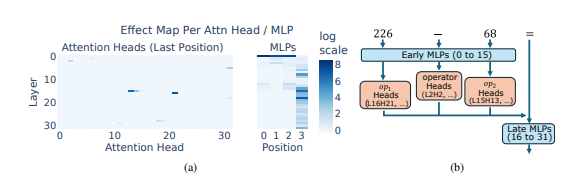
Lo que es aún más sorprendente es que esta estrategia de "mezcolanza heurística" en realidad apareció en las primeras etapas de la formación LLM y se mejoró gradualmente a medida que avanzaba la formación. Esto significa que LLM se basa en este enfoque de razonamiento “parcial” desde el principio, en lugar de desarrollar esta estrategia en una etapa posterior.
Entonces, ¿qué problemas causará este método de razonamiento aritmético "extraño"? Los investigadores descubrieron que la estrategia de "mezcolanza heurística" tiene una capacidad de generalización limitada y es propensa a errores. Esto se debe a que LLM tiene un número limitado de "pequeñas inteligencias", y estas "pequeñas inteligencias" en sí mismas también pueden tener fallas que les impiden dar respuestas correctas cuando encuentran nuevos patrones numéricos. Al igual que un chef que sólo puede hacer "huevos revueltos con tomate", si de repente le piden que haga "carne de cerdo desmenuzada con sabor a pescado", definitivamente tendrá prisa y se sentirá perdido.
Este estudio reveló las limitaciones de la capacidad de razonamiento aritmético de LLM y también señaló la dirección para mejorar la capacidad matemática de LLM en el futuro. Los investigadores creen que depender únicamente de los métodos de capacitación y la arquitectura del modelo existentes puede no ser suficiente para mejorar las capacidades de razonamiento aritmético de LLM, y es necesario explorar nuevos métodos para ayudar a LLM a aprender algoritmos más potentes y generales para que puedan convertirse verdaderamente en "maestros de las matemáticas".
Dirección del artículo: https://arxiv.org/pdf/2410.21272
Esta investigación no solo explica las deficiencias de LLM en los cálculos matemáticos, sino que, lo que es más importante, proporciona una valiosa dirección de referencia para futuras mejoras en LLM. Las investigaciones futuras deben centrarse en cómo mejorar la capacidad de generalización y la capacidad de aprendizaje de algoritmos de LLM para resolver sus deficiencias en el razonamiento aritmético y hacer que realmente posea poderosas habilidades matemáticas.