Bosonic est une bibliothèque développée pour la simulation de systèmes photoniques dont les entrées sont des bosons indiscernables (dans le cas qui intéresse les auteurs, des photons). En particulier, il se concentre sur le calcul rapide des fonctions de transfert multiparticules pour ces systèmes et prend en charge le calcul du gradient d'une fonction de coût par rapport aux paramètres du système. Il a été initialement développé pour le développement de nos réseaux de neurones optiques quantiques [1] et contient des fonctionnalités spécialisées pour leur simulation et leur optimisation.
Les principaux objectifs de cette bibliothèque étaient doubles :
La principale motivation de ce package était le calcul rapide de la transformée unitaire multiparticulaire en fonction de l'unitaire de particule unique et du nombre d'entrées bosoniques. Autrement dit, si nous avons un U unitaire à quatre dimensions et que nous savons qu'il y a 3 photons à l'entrée, nous voulons connaître la transformation sur le
Ceci est soutenu par la fonction bosonic.aa_phi , qui porte le nom d'Aaronson et Arkhipov, qui ont spécifié la forme de cette fonction que nous utilisons comme fonction Φ(U) dans [2]. Par exemple, nous pouvons démontrer le fameux effet Hong-Ou-Mandel avec un séparateur de faisceau :
>> > import bosonic as b
>> > import numpy as np
>> > U = np . array ([[ 1 , 1 ], [ 1 , - 1 ]], dtype = complex ) / np . sqrt ( 2 )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU )
[[ 0.5 + 0.j 0.70710678 + 0.j 0.5 + 0.j ]
[ 0.70710678 + 0.j 0. + 0.j - 0.70710678 + 0.j ]
[ 0.5 + 0.j - 0.70710678 + 0.j 0.5 + 0.j ]]
>> > print ( b . fock . basis ( 2 , 2 ))
[[ 2 , 0 ], [ 1 , 1 ], [ 0 , 2 ]]
>> > input = np . array ([[ 0 ], [ 1 ], [ 0 ]], dtype = complex )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU . dot ( input ))
[[ 0.70710678 + 0.j ]
[ 0. + 0.j ]
[ - 0.70710678 + 0.j ]]
>> > print ( np . abs ( phiU . dot ( input )) ** 2 )
[[ 0.5 ]
[ 0. ]
[ 0.5 ]]Ici, nous construisons l'unitaire correspondant à un séparateur de faisceau 50/50 dans U. Comme le montre la ligne après avoir imprimé phiU, la base ici est [2, 0], [1, 1] et [0, 2]. Ainsi, l'état correspondant à un photon incident à chacune des entrées est [0, 1, 0]. Dans la dernière ligne, deux lignes, nous voyons que la sortie est une superposition égale de deux photons à une sortie et de deux photons à l'autre, sans aucune probabilité que les photons sortent par des ports différents.
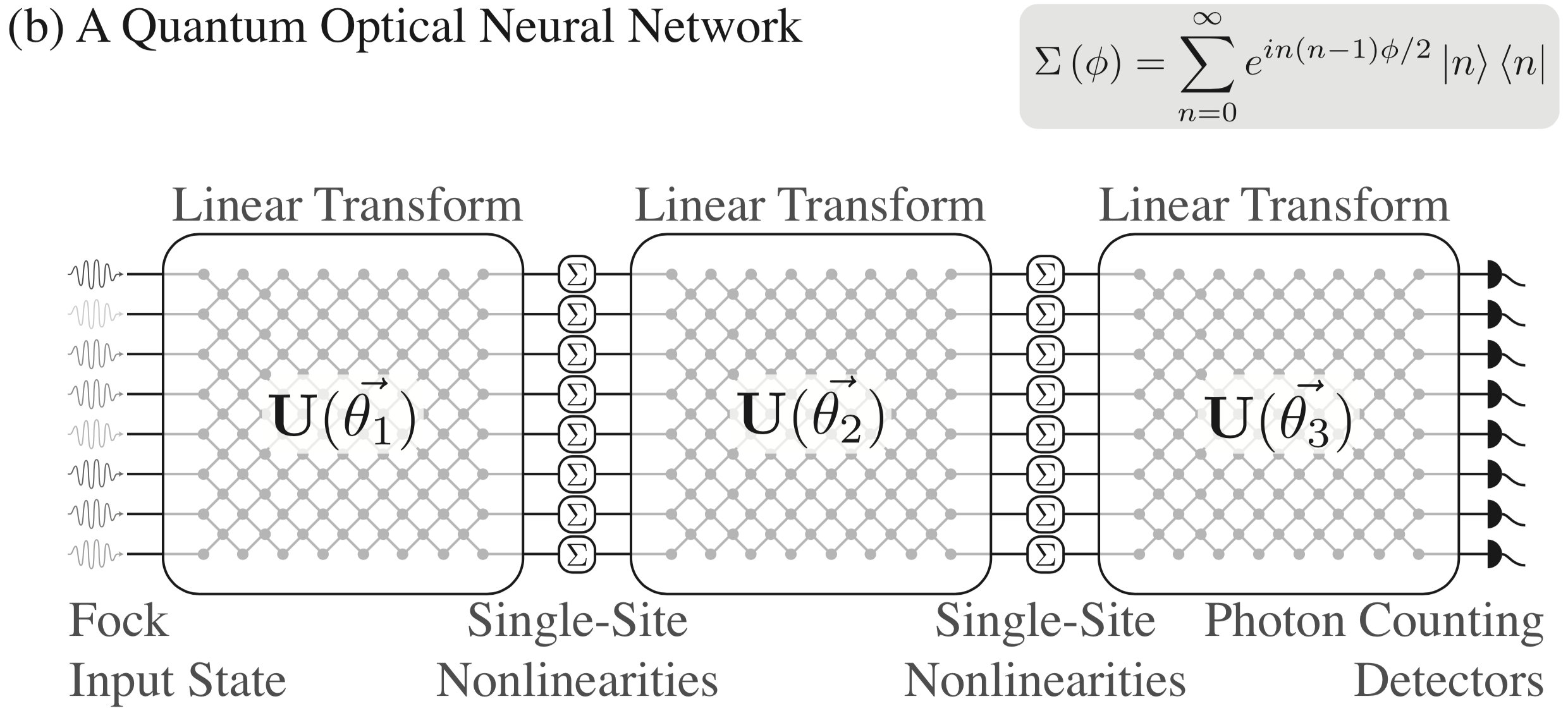
Comme décrit dans [1], nous avons développé une proposition d'architecture pour les réseaux de neurones optiques quantiques qui implique de mosaïquer des transformations unitaires arbitraires avec des non-linéarités à site unique. Consultez l'article pour plus de détails, mais voici un résumé visuel de l'architecture :
Le clonage de ce référentiel est actuellement le seul moyen d'obtenir bosonic sur votre système. Avant de faire cela, vous aurez besoin du package python Cython installé pour construire bosonic correctement. Quelque chose comme ceci devrait fonctionner sous Linux (en utilisant votre gestionnaire de packages Python préféré au lieu de pip , si vous le souhaitez) :
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .Sur Mac, vous aurez également besoin de gcc de homebrew et de libopenmp :
$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install . Vous devriez alors pouvoir tester que bosonic est correctement installé en exécutant
$ python setup.py test[1] Steinbrecher, GR, Olson, JP, Englund, D. et Carolan, J. (2018). Réseaux de neurones optiques quantiques. Préimpression arXiv arXiv:1808.10047. https://arxiv.org/abs/1808.10047
[2] Aaronson, Scott et Alex Arkhipov. "La complexité informatique de l'optique linéaire." Actes du quarante-troisième symposium annuel de l'ACM sur la théorie de l'informatique. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf