Tesla Stock Price Prediction

Analyse des séries chronologiques

• Prévisions boursières Tesla par modèles de séries chronologiques En obtenant les informations boursières de la société Tesla (NASDAQ : TSLA) via Yahoo Finance. Ce projet appliquera les méthodes d'analyse des séries chronologiques pour étudier les informations de base du TSLA et décomposer les séries chronologiques du TLSA.
• Les méthodes de lissage exponentiel pour prévoir le prix du TSLA dans les 365 prochains jours, puis utiliseront
• Le modèle ARIMA pour prédire le prix. Ce projet vérifiera également la distribution des erreurs. Ensuite, nous prévoyons la distribution des erreurs pour vérifier les performances du modèle.

Décomposer la série chronologique

Décomposer une série chronologique signifie la séparer en ses composantes constitutives, qui sont généralement une composante tendancielle et une composante irrégulière, et s'il s'agit d'une série chronologique saisonnière, une composante saisonnière. Pour les informations boursières TSLA, à partir du graphique de tendance des prix, nous pouvons voir qu'il n'y a pas de composante saisonnière dans les données. Mais ces données de séries chronologiques devraient inclure une composante tendancielle et une composante irrégulière. La décomposition de la série chronologique implique d'essayer de séparer la série chronologique en ces composantes, c'est-à-dire d'estimer la composante tendancielle et la composante irrégulière. Nous utiliserons la fonction SMA() pour lisser les données TSLA. Nous choisirons un ordre différent (n=8 et n=40) pour vérifier la composante tendance. Le but est d’essayer de lisser les données avec une simple moyenne mobile.

Modèle de prévision et évaluation : lissage exponentiel

• Modèle de lissage exponentiel
  Le modèle de lissage exponentiel peut être utilisé pour effectuer des prévisions à court terme pour les données de séries chronologiques. D’après les données TSLA, nous savons qu’il peut être décrit comme un modèle additif sans saisonnalité. À partir du graphique de tendance, nous pouvons voir que les fluctuations aléatoires de la série chronologique semblent avoir une taille à peu près constante au fil du temps. Nous utiliserons donc la fonction HoltWinter() pour ajuster une simple prédiction de lissage exponentiel.

Modèle de prévision et évaluation : modèle ARIMA

Modèle ARIMA

ARIMA (Autoregressive Integrated Moving Average) est un outil majeur utilisé dans l'analyse de séries chronologiques pour tenter de prévoir les valeurs futures d'une variable en fonction de sa valeur actuelle. Équation de prévision ARIMA(p,d,q) : les modèles ARIMA sont, en théorie, la classe la plus générale de modèles permettant de prévoir une série temporelle qui peut être rendue « stationnaire » par différenciation. Les modèles ARIMA sont définis pour des séries chronologiques stationnaires. Par conséquent, si vous commencez avec une série chronologique non stationnaire, vous devrez d'abord « différencier » la série chronologique jusqu'à obtenir une série chronologique stationnaire. Pour différencier les séries temporelles d fois afin d'obtenir une série stationnaire, nous utilisons la fonction diff(). Nous utiliserons ensuite le test ADF formel ne rejetant pas l'hypothèse nulle de non-stationnarité, confirmant notre inspection visuelle :

Résumé

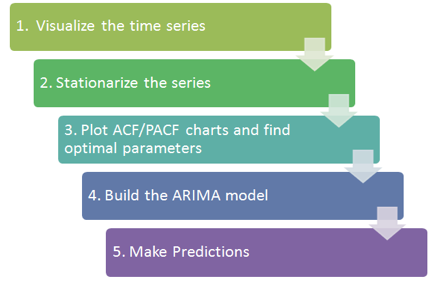
Dans cette section, nous utilisons les données boursières TESLA comme série chronologique. Nous le décomposons et utilisons le lissage exponentiel HoltWinter et ARIMA pour prévoir le cours futur de l'action. Les procédures de base sont présentées dans la figure suivante.

L'autre chose est que nous devrions toujours analyser les erreurs et ajuster les paramètres du modèle pour obtenir de meilleurs résultats.